개요
어제에 이어, ImageNet의 주요 모델(VGGNet 이후 모델)들과 semantic segmentation을 위한 다양한 기법들과 모델들에 대해 다루었다.
이 글은 아래와 같은 내용으로 구성된다.
여기서 다룬 내용들은 에서도 이미 다룬 적이 있다. 따라서 이전 포스트에 덧붙여 부족한 부분들을 위주로 작성할 예정이다.
Image classification(ImageNet)
더 깊은 네트워크는 더 큰 receptive field에 대한 다양한 고려가 가능하며(즉, 데이터에 대한 다양한 시각에서의 고려가 가능하며) 보다 다양한 형태의 함수를 만들어낼 수 있다. 하지만 네트워크가 deep해질수록 gradient vanishing/degradation problem이 발생한다. 이후 이를 해결하기 위한 다양한 방법이 제시되었다.
GoogLeNet
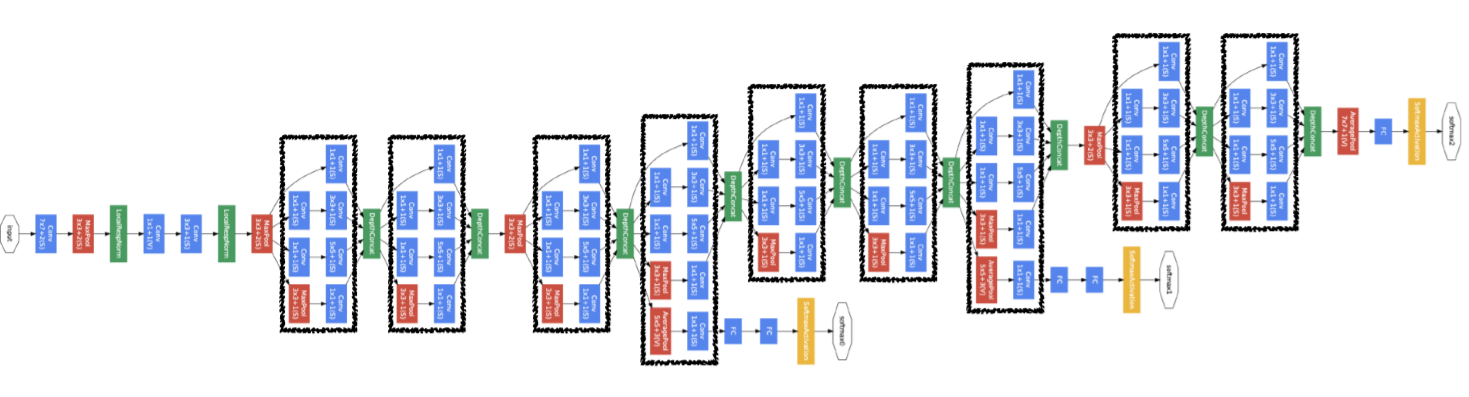
Inception module을 적용한 모델이다. VGGNet과 그 이전 모델들은 depth의 확장에 집중하였지만, 여기서는 width의 확장에 초점을 둔다.
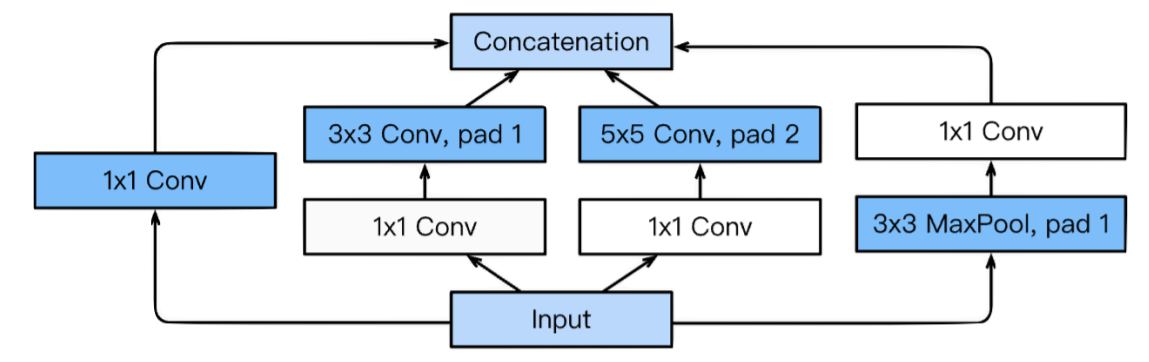
inception module은 다양한 size의 convolution을 통해 multi scale에 대한 지역 정보를 모두 고려할 수 있게 된다.
또한 convolution을 할 때 bottleneck architecture을 도입하여 computational resource을 줄인다.
처음에는 vanilla convolution networks(standard CNN), 이후 inception module을 stacking하는 형태로 이루어져있다.
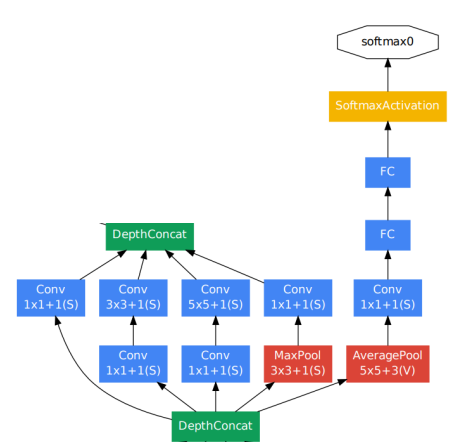
gradient vanishing에 대한 솔루션으로는 Auxiliary classifiers를 도입하였다.
이는 lower layers들에 추가적인 gradient 값을 주입시켜주는 역할을 한다. 모델 그림에서 중간중간 노란색으로 튀어나온 부분이 이러한 부분이다.
물론 이는 실제 classifing에 관여하지 않는다. 단지 gradient 전달을 위한 부분일 뿐이고, 실제 분류나 test 단계에서는 마지막 output만을 사용한다.
ResNet
ResNet은 skip connection을 통해 모델의 depth를 획기적으로 늘린 모델이다. depth가 깊어지면 모델의 성능이 하락(degradation)하는 경우가 있는데, ResNet에서는 이것이 단지 깊이가 깊어짐에 따라 나타나는 overfitting의 문제가 아님을 명시하였다.
여기서는 이것이 optimization의 문제라고 보았다. 즉, epoch을 많이 돌리면 학습이 되긴 할텐데 그 속도가 매우 느리다는 것이다.
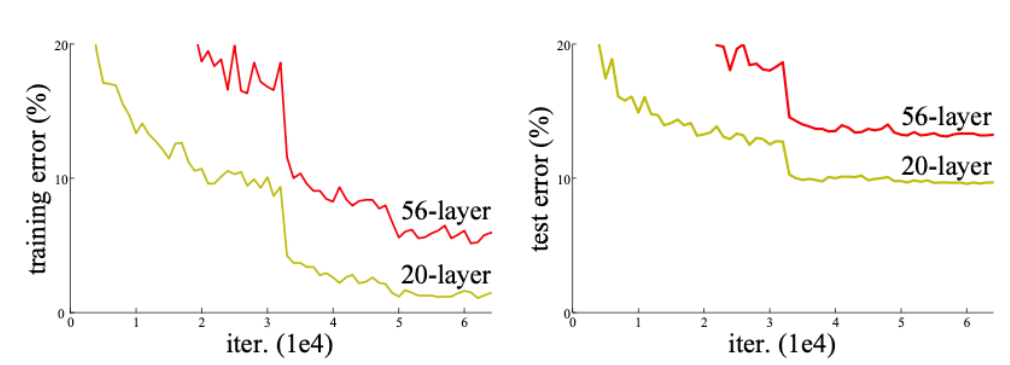
실제로 논문에서 제시된 그래프는 test error와 training error 사이의 간극이 보이지 않는다. 다만 그 절대적인 성능 자체가 좋지 않을 뿐이다.
그래서 사실 skip connection은 우리가 흔히 아는 gradient vanishing 문제를 해결할 뿐만 아니라, 학습 자체의 성능도 향상시킨다.
여기서 말하는 것은, 이미 $x$를 끝에 더해주기 때문에 모델은 $F(x) = H(x) - x$ 부분만 학습하면 된다는 것이다. 그런데 논문에서는 또한 모델 내에서는 identity mapping이나 이에 가까운, 즉 레이어 통과 전후의 값이 큰 차이가 없는 지점이 어느 순간부터 나타날 것이라는 가설을 세운다.
만약 위 가설이 맞다면, 모델이 학습하고자 하는 $F(x)$는 0에 가까워지게 된다. 따라서 매번 $x$를 다시 만들기 위해 쓸데없는 학습을 하지 않고 그 차이만을 학습하기 때문에 더 빠른 학습을 기대할 수 있을 것이다.
결국 위 가설이 어느정도 들어맞았고, 결국 shortcut connection은 vanishing을 해결할 뿐만 아니라 학습 자체의 optimization에도 큰 도움을 주었다.
residual connection, shortcut connection, skip connection 등 많은 용어를 활용하였는데 모두 같은 의미로 통용된다.
추가적으로 He initialization이라는 초기화 방법을 활용하였고, 3 x 3 conv만 하였으며, batch norm을 매 conv 이후마다 적용하였다. (conv-bn-relu)
DenseNet/SENet
DenseNet에서는 아래와 같이 Dense connection이 있는 DenseBlock 여러개를 두고 이를 통해 학습을 한다.
ResNet에서처럼 덧셈을 활용하지 않고 channel axis로 concatenation을 활용하였고, 모든 conv layer들을 각각 연결하였다. ($\frac{n(n+1)}{2}$개)
물론 계속해서 채널이 기하급수적으로 늘어날 수 있기 때문에 transition block에서 channel수를 hyperparameter theta 값을 통해 어느정도 줄여주기도 하였다.
SENet에서는 아래와 같이 일종의 attention 구조를 활용한다.
논문의 표현을 빌리자면 squeeze와 excitation을 적용하였다.
먼저 $\mathrm{F}_{sq}$는 global avgPooling을 말한다. 채널당 1 x 1 feature가 나오도록 pooling을 적용한다. (Squeeze) 다음으로, $\mathrm{F}_{ex}$라는 FC layer를 통과시켜 attention score을 담은 1 x 1 x C tensor를 얻는다. (Excitation)
마지막으로 attention score를 input으로 들어왔던 tensor(squeeze 하기 이전)에 곱해주어 중요도가 가중치로 적용된 최종적인 output을 얻는다.
attention은 이전에도 많이 봐왔지만 다른 모든 feature들을 고려한 연산을 하게 되므로 각자의 중요도가 보다 객관적으로 나올 수 있게 된다. 따라서 SENet에서의 방법론을 적용하면 전체 context에 대한 고려가 더 잘된 output이 출력될 것이라는 추측을 해볼 수 있다.
EfficientNet/Deformable convolution
EfficientNet에서는 위에서 생각해보았던 width scaling, depth scaling에 더불어 resolution scaling까지 모두 결합한 compound scaling 모델이다.
resolution scaling이란 애초에 해상도가 높은 이미지를 넣으면(즉 input이 큰 이미지를 넣으면) 성능이 좋을 것이라는 생각 하에 나오게 된 모델이다.
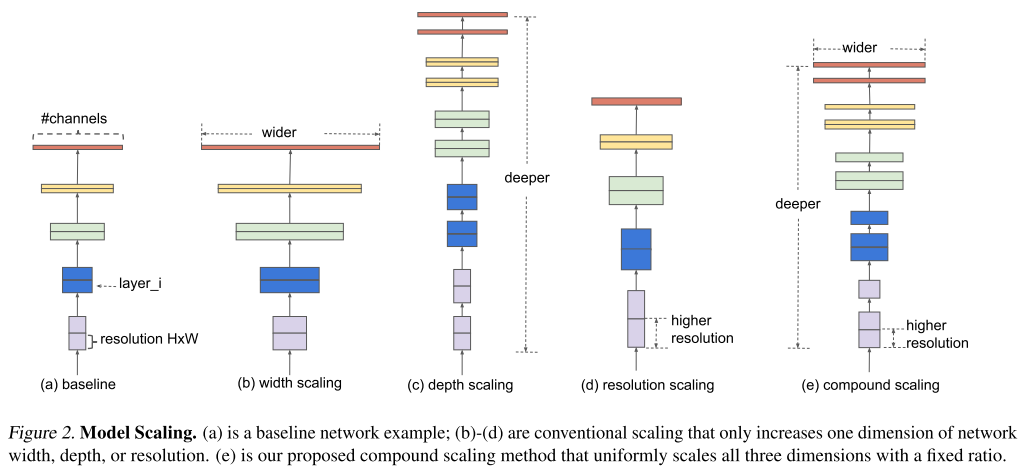
근데 단순히 이들 방법을 compound한다고 성능이 잘나오는건 아닐 것이다. 어떻게 이들을 섞을것인지 적절한 비율이 필요한데,
실제로 논문에서는 조작변인과 통제변인을 계속 바꾸어가며 이들 방법을 어떻게 섞을 것인지 실험을 진행하였고 이들의 최적 비율을 발견해냈다.
어떻게 이들을 섞었는지 자세한 설명은 일단.. 논문을 읽어보지 않았기 때문에 여기서 적진 않겠다. 다만, EfficientNet은 놀라울 정도로 적은 parameter 수와 FLOPS 수로도 기존 모델들을 훨씬 뛰어넘는 성능을 보이게 된다.
Deformable convolution은 SENet보다도 이전에 나온 방법론이지만, 그 방법론이 참신하기 때문에 수업에서도 다루었다. 여기서는 irregular convolution을 적용한다는 점이 가장 큰 특이점이다. irregular convolution은 단순한 2D conv가 아니라 2D offset이 더해진 2D conv를 활용한다.
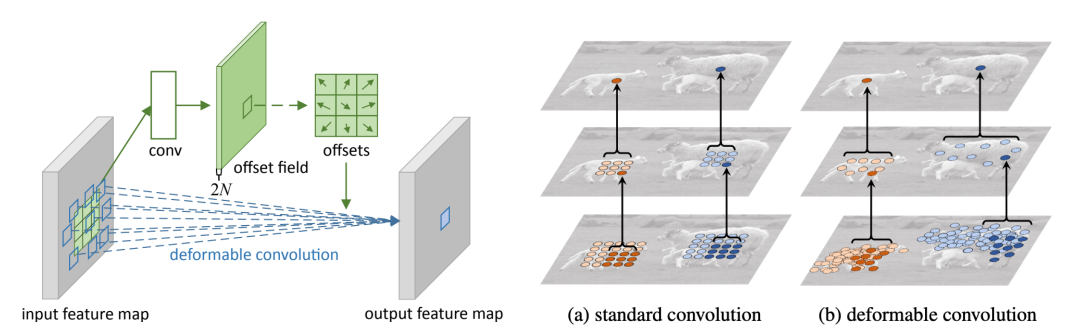
일반적인 conv layer의 가중치에 offset field에 의해 offset이 더해진다. 그러면 이 conv layer의 패턴이 단순 직사각형이 아니라 일그러지게 변한다.
이렇게 되면 샘플링 패턴이 좀 더 유연해지기 때문에(좀 더 정확히는, receptive field 크기가 고정되지 않기 때문에) receptive field가 좀 더 개별 이미지에 걸맞도록 짜여질 것이다.
여기서 적용되는 offset 역시 학습의 대상이다.
Semantic Segmentation
semantic segmentation은 이미지의 각 픽셀을 카테고리별로 분류하는 문제이다. 여기서 카테고리별 분류에 집중하기 때문에 서로 별개의 개체라도 그 개체들이 같은 클래스에 속한다면 모두 같은 segment로 분류된다. 이는 의료 이미지, 자율 주행, computational photography 등에 이용된다.
Fully Convolutional Networks(FCN)
지금부터는 semantic segmentation에 활용되는(활용되었던), 혹은 그 초석이 되었던 몇 개 모델들에 대해 알아보도록 하자.
FCN은 semantic segmentation에 있어 처음으로 end-to-end 구조를 가졌던 모델이다.
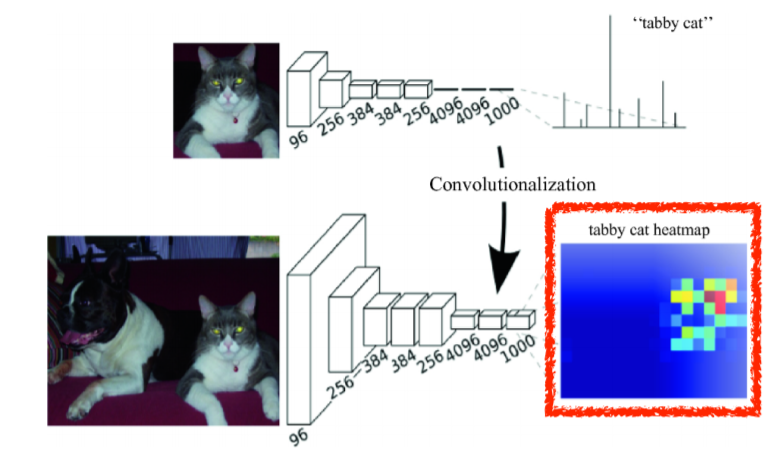
convolution만을 적용하였기 때문에 input size에 제약이 없으며 동시에 affine layer를 사용하지 않아 spatial information도 고려할 수 있다.
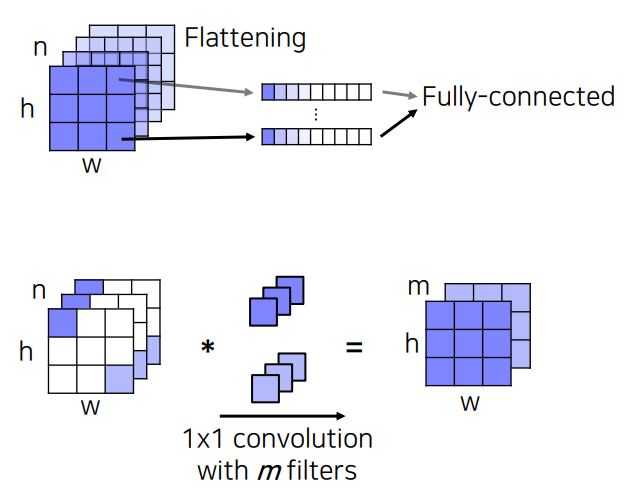
여기서는 affine layer를 conv layer로 대체하였는데, 실제로 1 x 1 conv layer는 affine layer와 동일한 역할을 한다.
그냥 쉽게 한 픽셀 단위로 보면 1 x 1 conv는 $(C, 1, 1)$을 $(C ^{\prime}, 1, 1)$로 바꾼다.
affine layer도 같은 의미를 가지는 linear transformation을 수행한다.
이를 모든 픽셀로 확장시키면 결국 두 레이어는 같은 transformation을 수행한다.
다만 affine layer는 모든 픽셀을 대상으로 하면 1 x 1 conv와 다르게 parameter를 훨씬 많이 써야 한다. 1 x 1 conv는 한 픽셀에 대해서만 하든, 모든 픽셀을 대상으로 하든 parameter 수가 똑같다. 따라서 1 x 1 conv는 연산량이 비교적 적다.
이렇게 두 레이어는 동일한 역할을 하지만, conv layer를 통과한 출력은 위치정보를 담고 있기 때문에 pixel별 값이 중요한 semantic segmenation과 같은 task를 할 때는 1 x 1 conv 연산을 활용하는 것이 아무래도 더 좋다.
이제 출력 map의 크기를 upsampling하는 과정에 대해 다루어보자. 이는 downsampling으로 인해 축소된 이미지 사이즈를 복원하는 과정이다.
만약 downsampling을 하지 않으면 픽셀별 receptive field가 작아져 영상의 전반적 context를 파악하지 못하는 문제가 발생한다. 따라서 downsampling은 필수적이고, 이를 어떻게 다시 upsampling 할 것인지에 대해 생각해보아야 한다.
upsampling을 위한 방법으로는 transposed convolution이 있다.
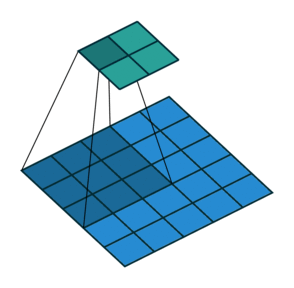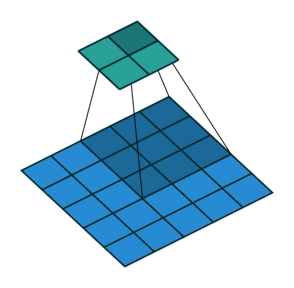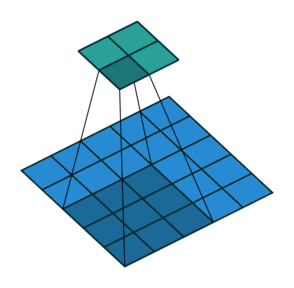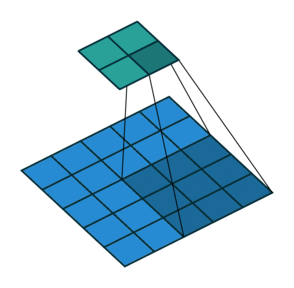
이 방법은 위 그림과 같이 동작한다. 늘리고자 하는 filter size로 원본 데이터를 transformation한 이후 그 값을 pixel별로 더해주면 되는 직관적인 방식이다.
보다 자세하고 실증적인 설명은 Reference를 참조하도록 하자.
standard한 transposed convolution 방법은 checkerboard artifact 현상이 일어나 특정 field에 값이 여러번 더해지는 문제가 발생한다.
이를 해결하려면 kernel size를 stride로 나눠지도록 설정해볼 수 있다. 이것에 대한 이유 역시 Reference에 기재된 글에 들어가보면 바로 이해할 수 있는데, kernel size가 stride로 나눠지면 projection이 균일하게 이루어지기 때문에 비교적 해당 현상이 덜하다.
다만 이 방법으로도 checkerboard artifact가 완전히 해소되지는 않아 이후 up-sampling을 convolution과 분리하는 방법이 제시된다.
이 방법이 최근 더 많이 쓰이는 방법인데 Nearest-neighbor(NN)이나 Bilinear interpolation 방법 등으로 이미지의 해상도를 늘린 후, 여기에 컨볼루션을 하는 방법이다.
interpolation은 ‘보간’이라는 뜻을 가지는데, 알려진 값 사이 중간값을 추정하는 기법이다. 이미지 확대 역시 중간 값을 예측하는 기술이다.
이러한 방법론을 이용하면 위와 같이 checkerboard artifact를 효과적으로 없앨 수 있다.
nearest neighbor interpolation은 아래와 같이 픽셀값을 주변으로 퍼뜨려주는 가장 간단한 테크닉이다.
Bilinear interpolation은 linear interpolation을 2차원으로 확장한 방법으로, 가중평균을 통해 구할 수 있다. 단순히 두 점이 있으면 그 중점값을 해당 픽셀로 사용한다는 직관적인 방식에 근거한 방법이다. (더 자세한 내용은 따로 찾아보기)
그리고 이러한 interpolation 방법을 적용한 후 convolution을 적용하면 된다. 그런데 어차피 여기서 쓰이는 두 interpolation 방법과 convolution 모두 linear operation이므로 행렬 하나로 이 연산 과정을 표현할 수 있다. 아무튼 이를 통해 checkboard artifact 현상을 피할 수 있는 효과적인 up-sampling이 가능하다.
이제 다시 FCN으로 돌아와서 보자. up-sampling을 한다고 해도 없어진 정보를 다시 완벽히 살리는건 어렵다. 그래서 각 레이어의 activation이 어떤 정보를 담고 있는지부터 다시 보도록 한다.
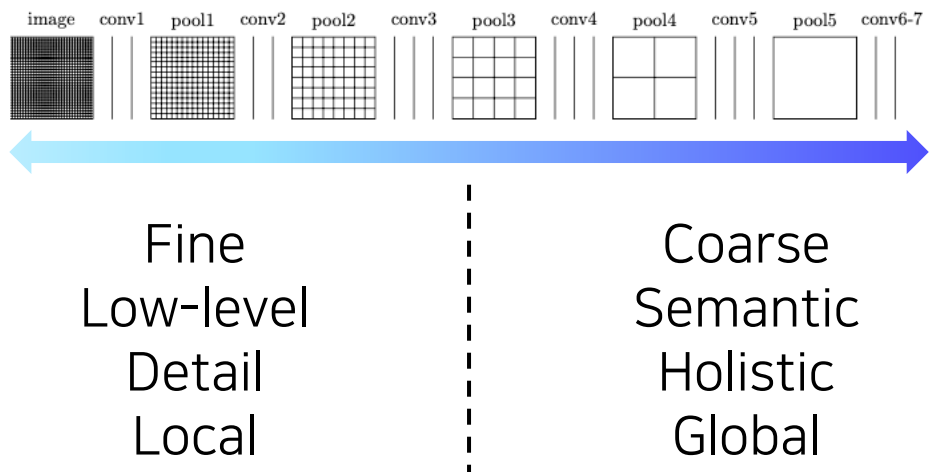
레이어 레벨별 activation(Conv의 출력)을 살펴보면 위와 같은 경향을 띤다.
earlier layer의 activation은 보다 자세하고, 국지적(local)인 정보를 담고있는 반면 latter layer의 activation은 보다 의미론적이고 전반적인 정보를 담고 있다.
그런데 우리는 이 둘 모두가 필요하다. 각 픽셀별 의미도 필요하고, 디테일한 경계부분도 필요하기 때문이다. 그래서 앞서 ResNet의 skip connection처럼 출력 단에서는 앞에서 나온 activation map을 가져와서 뒤에서 활용하게 된다.
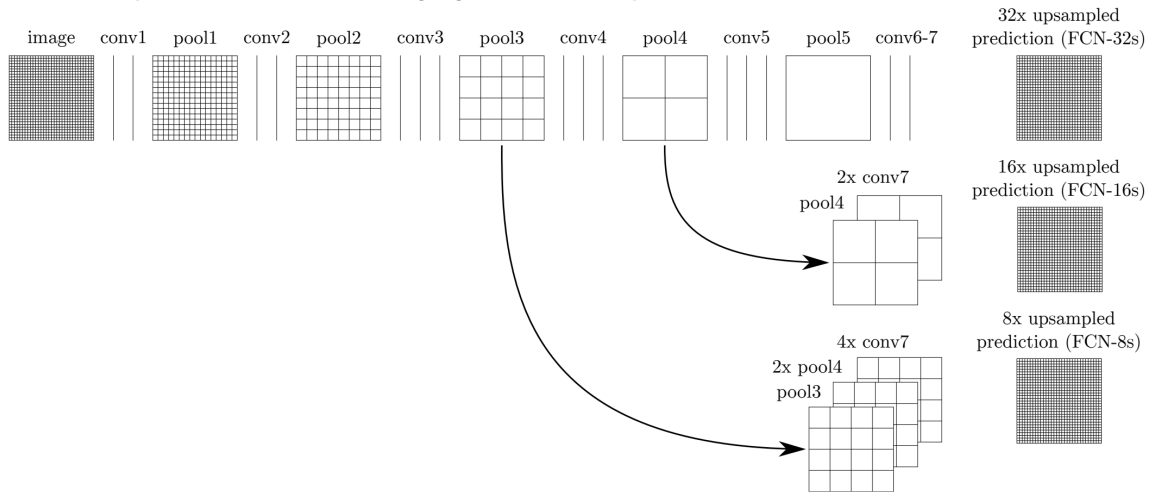
위 이미지에서 FCN-32s, FCN-16s, FCN-8s는 모두 다른 모델들인데, 각각 얼마나 앞선 activation을 가져오는지에 따라 구별된다.
그림에서 보이듯이 FCN-8s는 pool3, pool4, conv7을 모두 활용한다. 기준은 앞쪽 activation(pool3의 activation)이 되고 여기에 맞춰 그 뒤의 것들이 up-sampling이 된다.
그리고 이를 concatenation하여 최종적인 픽셀별 score 값을 얻게 된다.
당연히 FCN-8s의 성능이 가장 좋았으며, 논문에 따르면 결국 중간 단계의 activation map을 함께 활용하는 것이 큰 도움이 되는 것을 실험적으로 알 수 있었다.
비슷한 연구로 Hypercolumns for object segmentation이라는 논문이 있는데, 여기서도 거의 같은 방법론을 제시한다. 다만 여기서는 미리 서드파티 알고리즘으로 각 물체의 bounding box를 먼저 추출하고 이를 입력으로 활용했다는 차이점이 있다.
U-Net
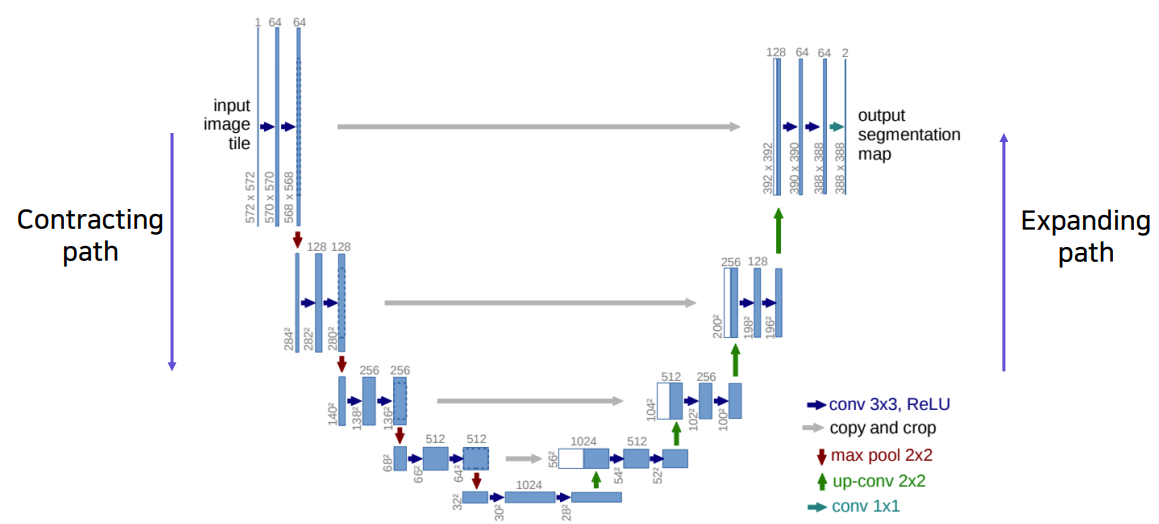
U-Net은 semantic segmentation의 새로운 breakthrough를 제시한 모델이다.
모델 구조는 어렵지 않다. 먼저 Contracting path(좌측)(=Encoding 과정)에서는 일반적인 CNN 모델처럼 feature map을 줄이고 channel을 늘리는 과정을 거친다. 여기서도 3 x 3 convolution과 2 x 2 maxPooling을 활용하였으며 channel 수와 feature size는 level별로 각각 2배씩 증가, 감소한다.
다음으로 Expanding path(우측)(=Decoding 과정)에서는 여기에 2 x 2 up-convolution을 통해 feature size를 다시 2배씩 늘린다. 또한 channel 수도 다시 3 x 3 conv로 2배씩 감소시킨다. 특이한 점은 이렇게 아래 level에서 다음 level input으로 넣어주는 feature map이 이전 contracting path의 같은 level 출력과 concat된다는 점이다. 이후 concatenation된 feature를 3 x 3 conv를 통해 다음 level의 channel 수에 맞춰준다.
2 x 2 up-conv는 PyTorch의
nn.ConvTranspose2d()레이어로 구현할 수 있다.
이렇게 하면 앞선 레이어에서 전달된 특징이 localized information 정보를 주므로 공간적으로 중요한 정보(segment의 경계선 등)를 뒤쪽 레이어에 바로 전달할 수 있게 된다.
한편 U-Net 모델을 돌릴 때 up-sampling과 down-sampling이 반복해서 적용되기 때문에 feature size를 잘 고려해야한다. 예를 들어 7 x 7 feature map은 2 x 2 maxPool 이후 3 x 3이 되는데, 이것이 다시 2 x 2 up-conv를 거치면 6 x 6이 된다. 이런 경우를 대비하여 up-sampling / down-sampling 시에 알고리즘을 어떻게 세울 것인지 유의해야할 필요가 있다.
U-Net은 FCN과 어느정도 유사한 형태이지만 보다 진보된 구조로, 적은 양의 학습 데이터만으로 Data augmentation을 활용하여 여러 biomedical segmentation task에서 우수한 성능을 보여주었다.
DeepLab
DeepLab 또한 semantic segmentation task에서 중요한 한 획을 그었던 모델로, 2015년 v1부터 2018년 v3+까지 발표되었다.
주요 특징으로는 CRFs(Conditional Random Fields)라는 후처리와 Dilated Convolution(Atrous Convolution)라는 convolution operation을 활용한다는 점 등이 있다.
먼저 CRFs(Conditional Random Fields)부터 살펴보자.
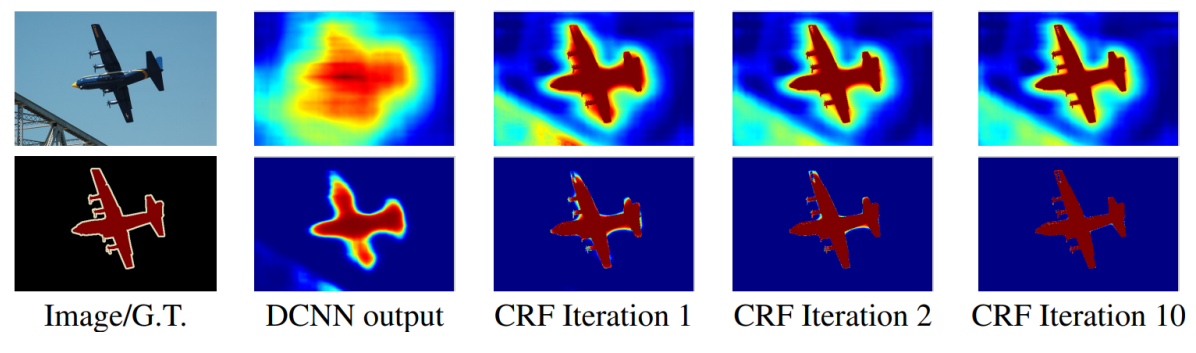
여기서 쓰인 CRFs는 정확히는 fully-connected CRF인데, 자세한 내용은 reference를 참조하자.
이 부분을 이해하려면 일단 CRF에 대해 이해하고 다음에 fully-connected CRF의 강점에 대해 이해한 후 이것을 고속연산할 수 있었던 방법론에 대해 알아보아야 한다.
하지만 이 모든 것을 보기에는 지금 당장은 시간이 없다 
그래서 일단 이 부분은 숙제로 남겨두도록 한다.
간단하게만 요약하면 fully-connected CRF는 후처리 작업인데 이를 적용할 시 앞선 convolution(Dilated CNN) 연산의 결과로 나온 feature map에서 boundary를 위 그림과 같이 더 확실하게 그어줄 수 있게 된다. 근데 이것도 DeepLab v2까지만 활용했고 v3부터는 활용하지 않고도 정확한 boundary를 잡아내었다.
다음으로 Dilated Convolution(Atrous Convolution)은 아래 그림 우측과 같이 convolution할 때 dilation factor만큼 픽셀 사이 공간을 넣어준 채로 연산을 수행한다. (여기서는 stride=2)
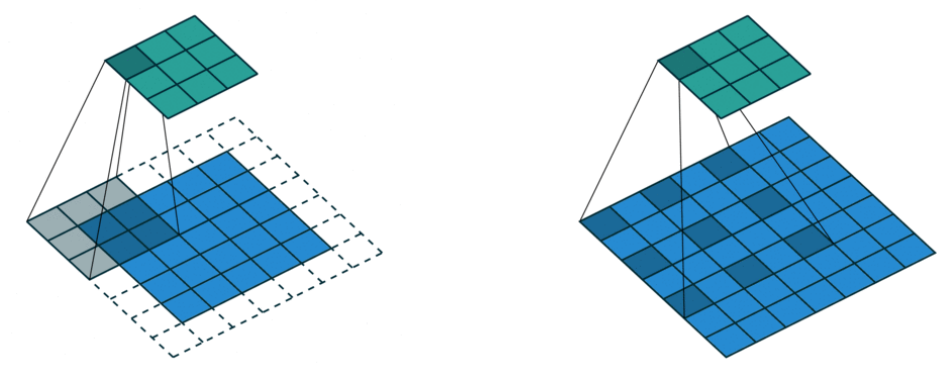
이렇게 하면 좌측과 같은 standard conv 연산보다 더 넓은 영역을 고려할 수 있게 된다. (=더 넓은 receptive field)
그런데 parameter수는 늘어나지 않으므로 같은 parameter만으로도 receptive field를 exponential하게 확 증가시키는 효과를 얻을 수 있게 된다.
DeepLab v3+부터는 들어오는 입력 이미지의 해상도가 너무 커서 computational cost를 줄이기 위해 depthwise separable conv와 atrous conv를 결합한 atrous separable conv를 사용하게 된다.
depthwise separable conv는 아래와 같이 conv연산이 채널별 conv와 채널 전체 단위 conv로 나뉘게 된다.
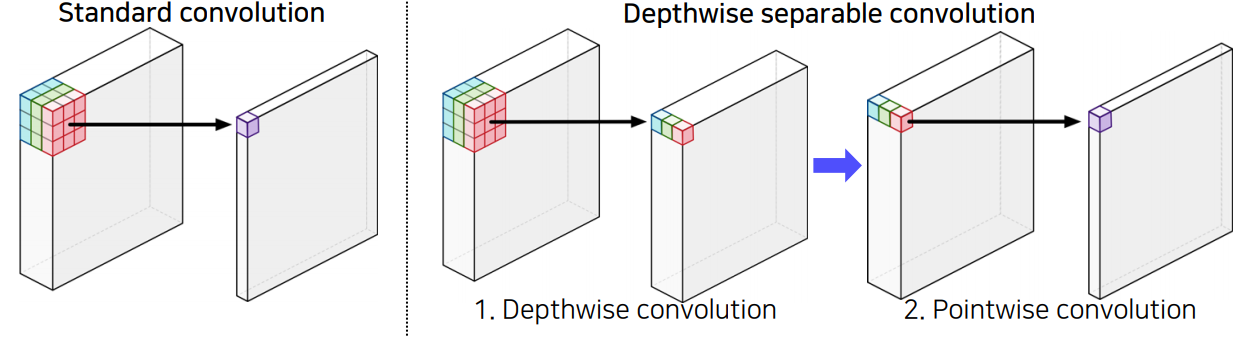
이렇게 하면 $D_K$와 $D_F$가 각각 kernel, feature map size이고 $M$, $N$이 각각 입력, 출력 채널 수 일때
parameter수가 기존 $D_K ^2 MND_F ^2$에서 $D_K ^2 M D_F ^2 + MND _F ^2$로 감소하게 된다.
참고로 이는 MobileNet 논문에서 이전에 제시된 기법인데, 이를 그대로 활용하였다.
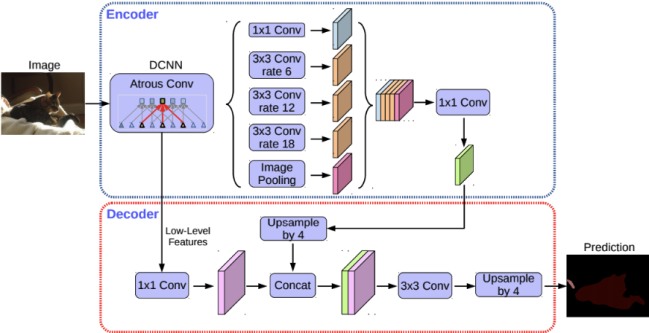
그 외 DeepLab v3+에서는 아래와 같은 특징을 가진다.
- U-Net의 Encoder-Decoder 구조를 활용 (Encoder(backbone)에 Xception 기반 모델 사용, Decoder에 U-Net 기반 모델 사용)
- 맨 가운데 부분처럼 Atrous Spatial Pyramid Pooling(ASPP) 기법 (multi-scale context에서 conv하여 concatenation하는 기법) 활용
- CRFs 구조 없이 거의 완전한 boundary 탐색 (boundary는 v2까지만 활용)
Reference
Deformable Convolutional Networks
Up-sampling with Transposed Convolution
Deconvolution and Checkerboard Artifacts
Nearest Neighbor Interpolation
선형 보간법(linear, bilinear, trilinear interpolation)
Dense CRFs
DeepLab