Day13. CNN and Vision

CNN과 컴퓨터 비전에서의 딥러닝

Posted by MoonJaeHoon on February 03, 2021 · 16 mins read

개요

어제 공부했던 convolution을 적용한 CNN 모델과 이를 컴퓨터 비전에 어떤 방식으로 적용하였는지에 대해 간단하게 배웠다.

오늘은 아래 내용을 다루었다.


CNN(Convolutional Neural Network)

어제도 언급하였는데, 3차원 convolution에서 커널(필터)과 input의 채널수가 같아야 한다는 점을 항상 명심하자.
물론, output의 channel수는 커널 한 개당 한 개가 나오게되므로, output으로 여러 채널을 얻고 싶다면 커널수를 늘리면 된다.
당연히, 커널수가 늘어나면 그만큼 parameter수도 늘어나게 된다는 점을 기억하자.

Convolution

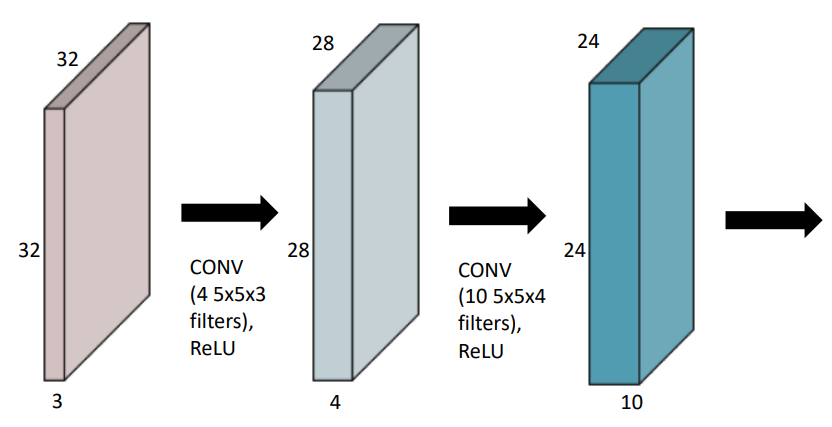
example_convolution

각 파트에서 커널의 특징이 주어지는데, 맨 왼쪽 값은 커널의 개수, 그 뒤는 각각 너비, 높이, 채널수를 의미한다.
output의 채널은 커널의 개수만큼 나오게 된다.


고전적인 CNN

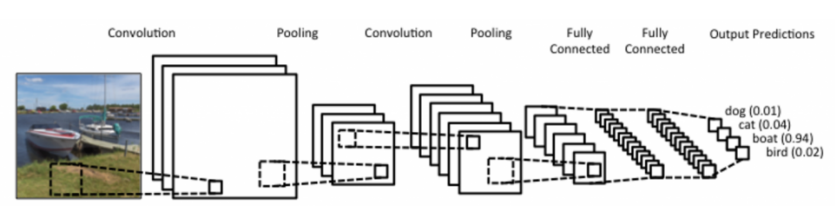
example_cnn
위 그림은 가장 고전적, 기본적 CNN 구조이다. convolution/pooling layer들에서는 feature extraction(특징 추출), affine layer들에서는 결정(decision making)을 한다. convolution, pooling을 여러번 반복하고 뒤에서는 우리가 전에 다루었던 affine layer가 나오게 된다. parameter수가 많을수록 학습이 어렵고 generalization performance가 떨어지기 때문에 parameter수를 줄일 방법에 대해 연구가 필요하다.

최우선적으로, 많은 parameter가 affine layer 부분에 존재하기 때문에 affine layer의 수를 최대한 줄이는 것이 좋다.
실제로 요즘은 CNN에서 affine layer를 줄이고, convolutional layer를 많이 가져가는 방향으로 발전하고 있다.

parameter 개수는 CNN의 중요한 평가지표 중 하나이므로 어떤 모델을 보았을 때 해당 모델의 파라미터가 대충 몇개일 지 가늠할 수 있는 감을 키우는게 중요하다.


Stride, Padding

stride는 커널이 몇 칸씩 건너뛰면서 특징추출을 할지 결정하는 파라미터이며, 패딩은 특징추출시 input의 가장자리에 얼마나 0을 채울지 결정하는 파라미터이다. padding을 겉에 둘러줌으로써 output의 spatial dimension(가로, 세로)을 기존보다 늘려줄 수 있다.

패딩은 보통 input과 output의 spatial dimension을 같게 해주고 싶을 때 많이 사용한다.
$k$가 커널의 사이즈이고 홀수일 때, input과 output의 크기가 같게 하려면 패딩 사이즈 $p = \lfloor{\frac{k}{2}}\rfloor$이다.
이것은 간단하게 증명할 수 있는데, 패딩 size 1당 output의 한 변 길이가 1씩 늘어나게 되므로 output의 한 변의 길이는 $n + 2p - k + 1$이고 원하는 것은 $n + 2p - k + 1 = n$이므로 $p = \frac{k - 1}{2} = \lfloor{\frac{k}{2}}\rfloor$이다.

참고로, 위 식에 따라 $k$(커널 사이즈)가 짝수이고 패딩이 일정하면 input과 output이 같아질 수가 없는데, 그래서 보통 커널 값은 홀수라고 한다.


CNN과 parameter

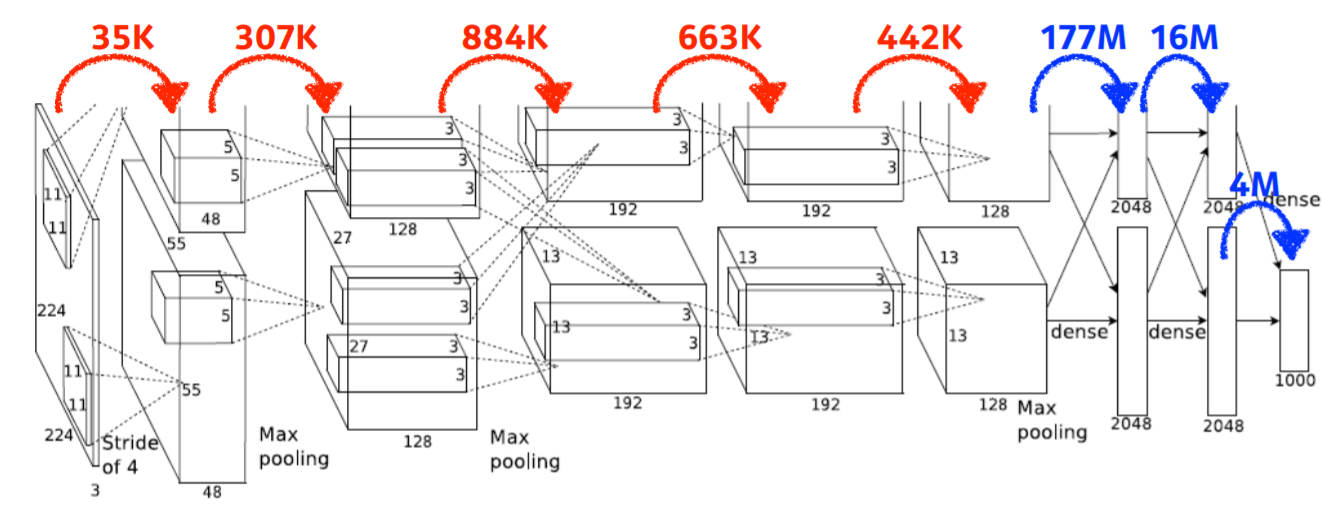
cnn_parameter
위 그림은 AlexNet에서 각 레이어별로 parameter수를 구해놓은 예시이다.
AlexNet이 나올 당시 GPU의 성능이 부족했기 때문에 분기를 2개로 나눠놓았지만, 결국 계산은 같다.

간단하게 몇개만 구해보자. affine layer는 fully connected layer(dense layer)를 뜻한다.

  • 1th convolution
    • 커널의 사이즈가 11 x 11이고 채널은 3이다. (보통 커널의 채널수는 input의 채널과 같아야하므로 생략하는 경우가 많다.)
    • output의 채널이 48이므로 커널의 개수도 48이어야하며, 분기가 2개로 갈라지므로 이를 2번 카운팅해야한다.
    • 따라서 여기서의 총 parameter수는 $11 \times 11 \times 3 \times 48 \times 2 = 34848$
    • affine layer와 다르게, 여기서의 parameter수는 input의 size에 의존적이지 않다는 점을 다시 한번 짚고 넘어가자. (224와 아무 관련이 없다)
  • 3th convolution
    • 다른 곳들과 다르게 여기서는 interchange가 일어나므로 $\times 2$가 아니라 $\times 4$를 해줘야한다.
    • 따라서 계산해보면 $3\times3\times128\times192\times4 = 884736$
  • 1th affine layer(6th layer, fully connected)
    • 기존과 같이 parameter가 input, output 모두의 size에 의존적이다.
    • 여기서는 생략되었지만, convolutional layer의 output을 affine layer에 input으로 넣어주기 위해 flatten(쫙 펴주는) 작업도 필요하다.
    • $13\times13\times128$개의 parameter 2세트가 input으로 들어가 2048개의 output 2세트가 나온다.
    • 계산해보면 $13 \times 13 \times 128 \times 2 \times 2048 \times 2 = 177209344$
  • 3th affine layer(8th layer, fully connected)
    • 동일한 방법으로 $2048 \times 2 \times 1000 = 4096000$개의 parameter가 나오게 된다.

딱 봐도 affine layer에서 parameter 개수가 월등히 많다.
convolutional layer에서는 커널의 크기가 input 크기와 독립적이기 때문에 parameter가 상대적으로 덜필요하다.


Modern CNN - 1 x 1 convolution

최근의 CNN에서는 1 x 1 convolution(1 x 1 kernel)을 거의 반드시 사용한다.
1 x 1 convolution은 spatial dimension은 유지하되, channel dimension을 줄이는 효과가 있다.

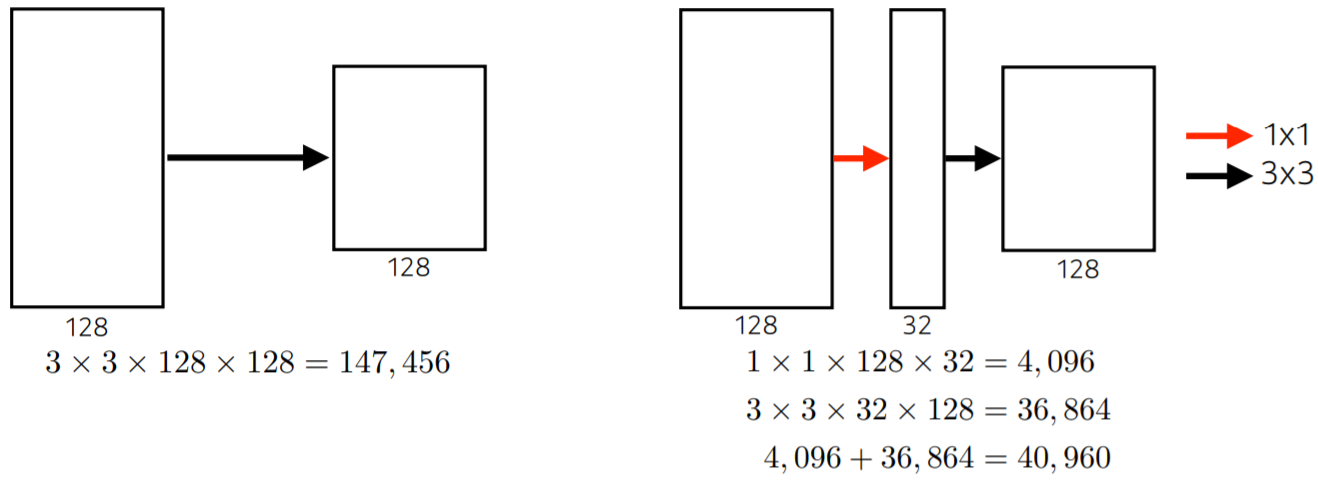1_1_convolution channel 수를 줄이고 convolution을 수행하는 것이 필요한 parameter를 대폭 줄일 수 있다.

그래서 이것을 이용하면 신경망의 깊이를 깊게 하면서 오히려 parameter의 개수는 줄일 수 있다.

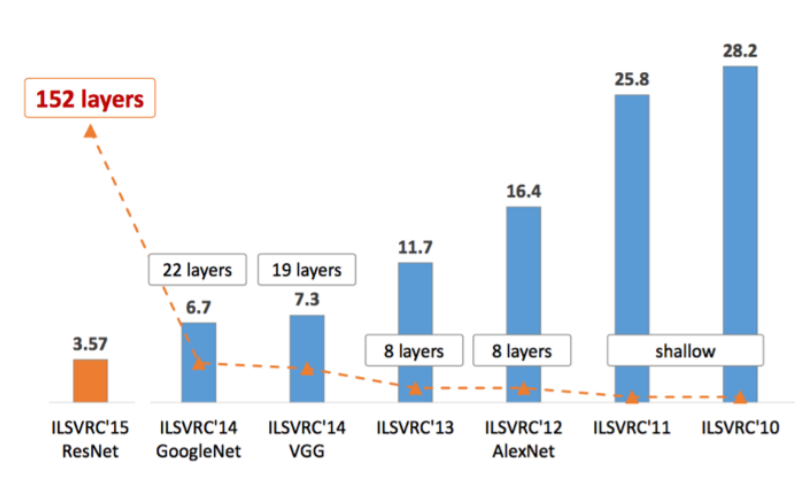
cnn_plot
역사적으로 유명했던(역사 자체가 얼마 안되긴 했지만..) 신경망의 layer수와 오류율(숫자가 낮을수록 높은 성능)을 나타낸 차트이다.
보다시피, 성능이 좋을수록 layer수(depth)가 대체로 많아지는데 이 과정에서 1 x 1 convolution layer가 들어가게 된다.
또한, 위에서 기술하였듯이 depth가 깊을수록 parameter 개수가 오히려 줄어드는 경우도 있다.


AlexNet

딥러닝의 포문을 연 모델으로, 지금까지도 쓰이는 많은 기법들이 여기서 유래한다.

  • ReLU 함수를 사용
    • ReLU는 선형의 특징을 어느정도 유지하는 비선형 활성함수이다.
    • 선형(linear) 특성을 지니고 있어 gradient descent가 간편하다.
    • sigmoid, tanh에서의 vanishing gradient(gradient가 옅어져 사라지는 현상)가 여기서는 나타나지 않는다.
  • GPU를 2개 병렬 연결하여 사용하였다.
  • Local response normalization(LRN) 기법을 사용하였다.
    • LRN은 현재는 잘 사용하지 않는 기법으로, ReLU사용으로 인해 매우 큰 input이 억제되지 않는 상황에서 정규화(국소적 정규화)를 해준다.
    • 현재는 Batch Normalization을 더 널리 사용한다.
  • Data augmentation, Dropout 기법을 사용하였다.


VGGNet

  • 3 x 3 kernel(with stride 1)을 사용하였다.
    • 기존 AlexNet에서는 11 x 11을 사용했었으나 사실 kernel size는 너무 크면 좋지 않다.
    • kernel size가 커지면 receptive field가 커진다. (receptive field는 output 한 칸에 영향을 주는 input layer의 spatial dimension이다.)
    • 하지만 작은 size의 kernel을 여러 개 사용하면 큰 size의 kernel과 같은 receptive field를 가질 수 있다.
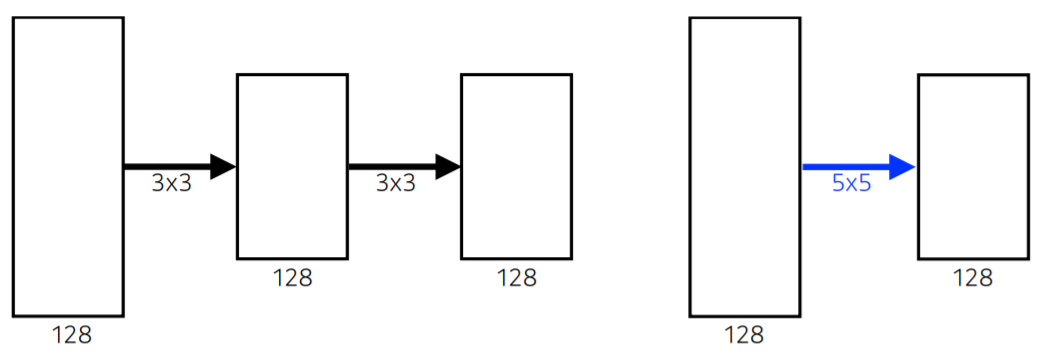
    • 예를 들어, 아래와 같은 그림에서 3 x 3 kernel 두 개를 sequential하게 연결하면 5 x 5 한 개일때와 receptive field가 같다. why3_3
    • 그런데 parameter 수는 좌측이 $3 \times 3 \times 128 \times 128 \times * 2 = 294912$, 우측이 $5 \times 5 \times128 \times 128 = 409600$으로 우측이 더 크다.
    • 이와 같이 일반적으로 같은 receptive field를 표현하더라도, 작은 kernel을 여러개 쓰는 것이 parameter 개수 측면에서 더 유리하다.
    • 그래서 요즘 나오는 논문들은 웬만해서는 커널 사이즈가 7 x 7을 넘지 않는다고 한다.
  • 1 x 1 convolution을 사용하였는데, 여기서 사용된건 사실 parameter 수 줄이려고 넣은 건 아닌 듯하다.
  • Dropout($p=0.5$)를 사용하였다.


GoogLeNet

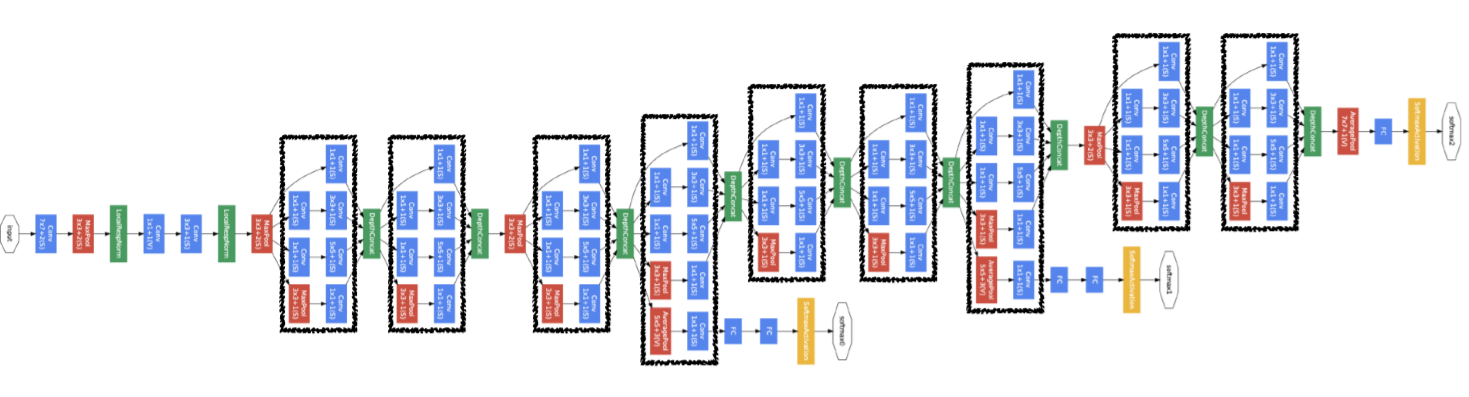
google_net

  • NiN(Network in Network) 구조를 채택하였다. NiN은 같은 네트워크 구조가 반복되는 것으로, 위에서 네모 표시가 된 부분이 반복된다.
  • 그리고 이 반복되는 부분은 모두 Inception 구조로, GoogLeNet의 핵심이다.
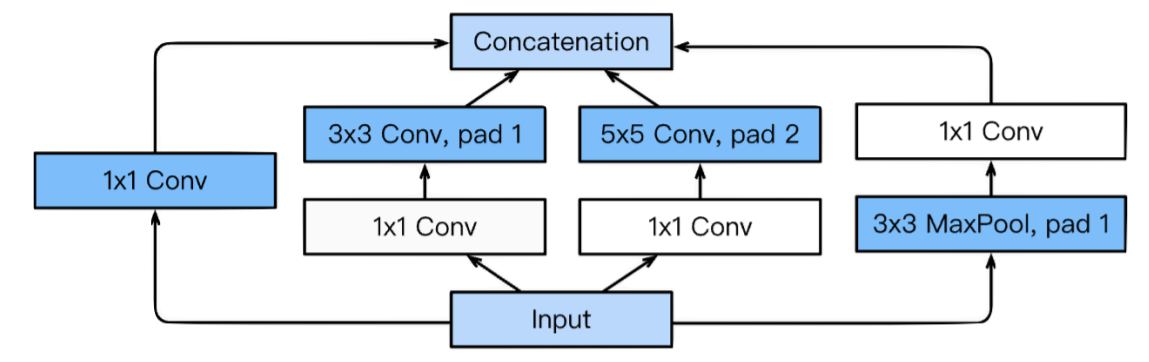
  • Inception 구조(Inception Block) google_net_inception
    • 하나의 입력이 여러 개로 퍼지고 다시 하나로 합쳐지는 구조이다.
    • feature를 효과적으로 sparse하게 추출하기위해 여러 다른 크기의 kernel을 사용하여 convolution을 여러번 수행한다.
    • 연산량이 너무 많아질 것을 방지하기 위해 1 x 1 convolution 연산을 활용하여 parameter의 개수(혹은 channel)을 대폭 줄였다.
    • 다른 것들과 spatial dimension, channel수 등을 모두 맞춰주기 위해 Pooling에도 padding과 1 x 1 convolution이 있는 것이 재미있는 특징이다.


ResNet

층이 너무 깊어지면 overfitting 등의 현상으로 오히려 성능을 저해할수도 있다는 우려를 해결한 모델이다.

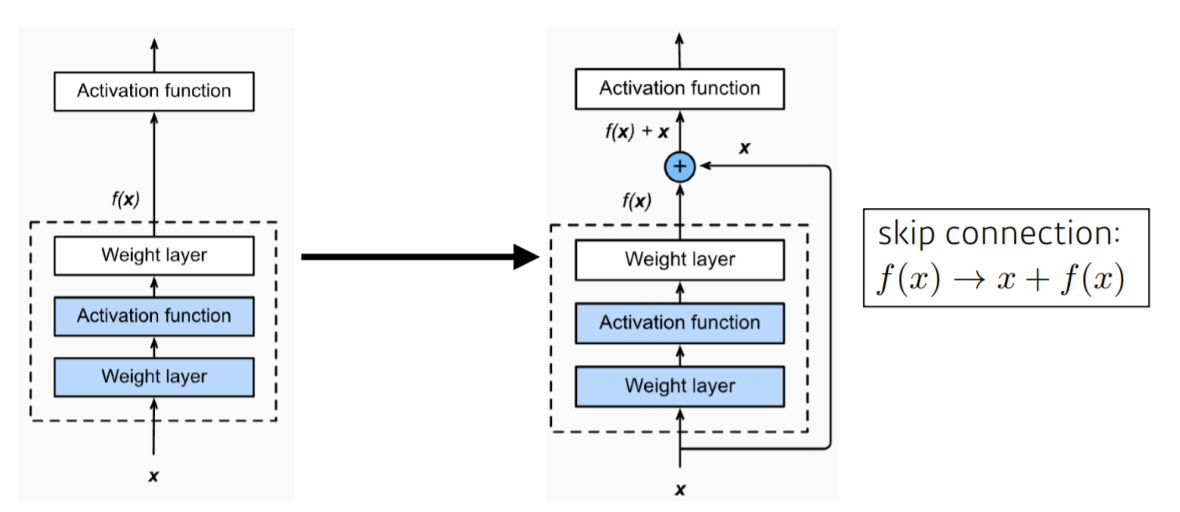
  • 스킵 연결(skip connection)을 도입하여 위와 같은 문제를 해결하였다. skip_connection
    • 위와 같이 입력 데이터를 출력에 더해준다.
    • 층이 깊어지면 학습이 잘 안될 것이라는 우려는 근본적으로 역전파의 chain rule에서 1보다 작은 값들 때문에 발생한다.
    • 그런데 skip connection을 이용하면 이전 chain만큼의 값이 더 더해지는 것이 보장되므로, 역전파에서 신호가 감쇠되는 효과를 막아줄 수 있다.
    $$ \text{output} \; H(x) = F(x) + x $$ $$ \frac{\partial L}{\partial x } = \frac{\partial L}{\partial H} \frac{\partial H}{\partial x} = \frac{\partial L}{\partial H} ( \frac{\partial F}{\partial x} + 1 ) = \frac{\partial L}{\partial H} \frac{\partial F}{\partial x} + \frac{\partial L}{\partial H} $$
    • 참고로 여기서 weight layer는 그냥 convolutional layer라고 생각하면 된다.
    • 이 글에도 좋은 설명이 있는 것 같다. 요약하면, 이미지 분류 문제의 경우 사실 입력 $x$에 대한 타겟값 $y$는 $x$를 대변하는 것으로 $y$와 $x$의 의미가 같게끔 mapping해야 한다. 따라서 네트워크의 출력값이 $x$가 되도록 $H(x) - x$를 최소화하는 방향으로 학습을 진행해야한다는 것이다.

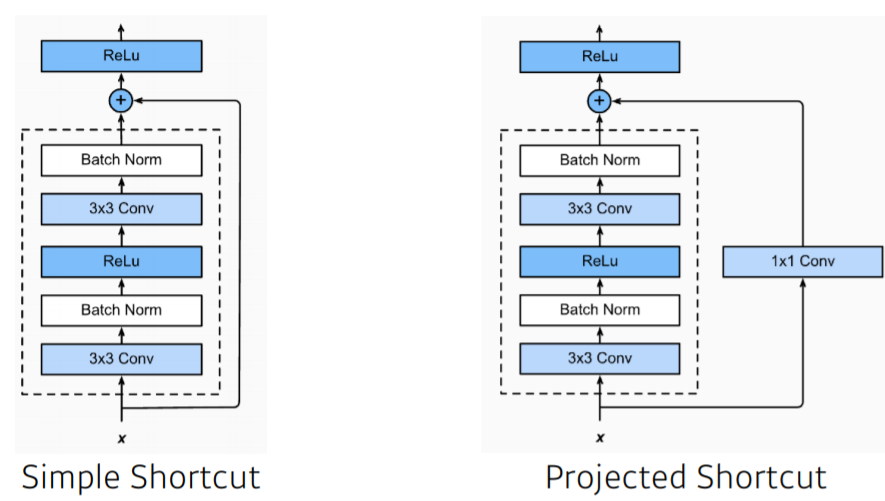
projected_shortcut

  • $x$를 $f(x)$에 더해주려면 둘의 dimension(channel)이 같아야 하므로 이를 위해 x에 1 x 1 convolution을 하고 더해준다. (projected shortcut)
  • convolution 이후 Batch normalization이 이루어진다. 최근에는 이 순서에 대한 논란도 있다고 한다.
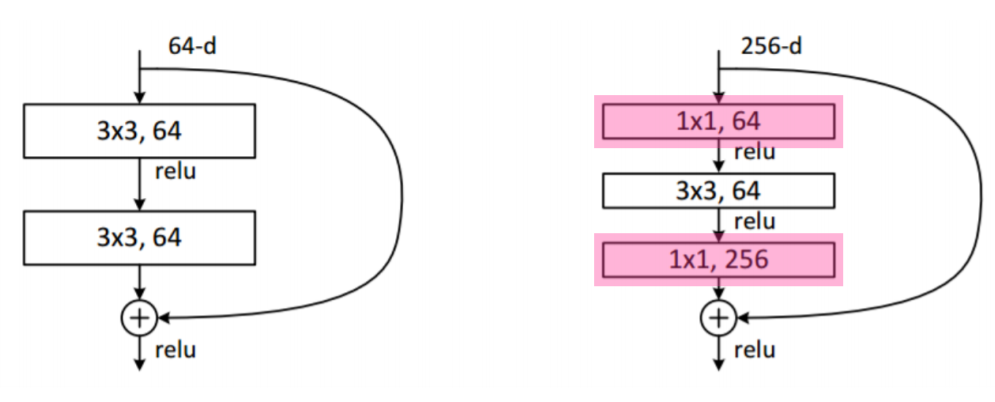
  • Bottleneck architecture를 도입하였다. bottleneck_architecture
    • 3 x 3 convolution을 할 때 연산량을 줄이기 위해 1x1 convolution으로 축소 후 연산, 이후 다시 확장하는 과정을 거친다.


DenseNet

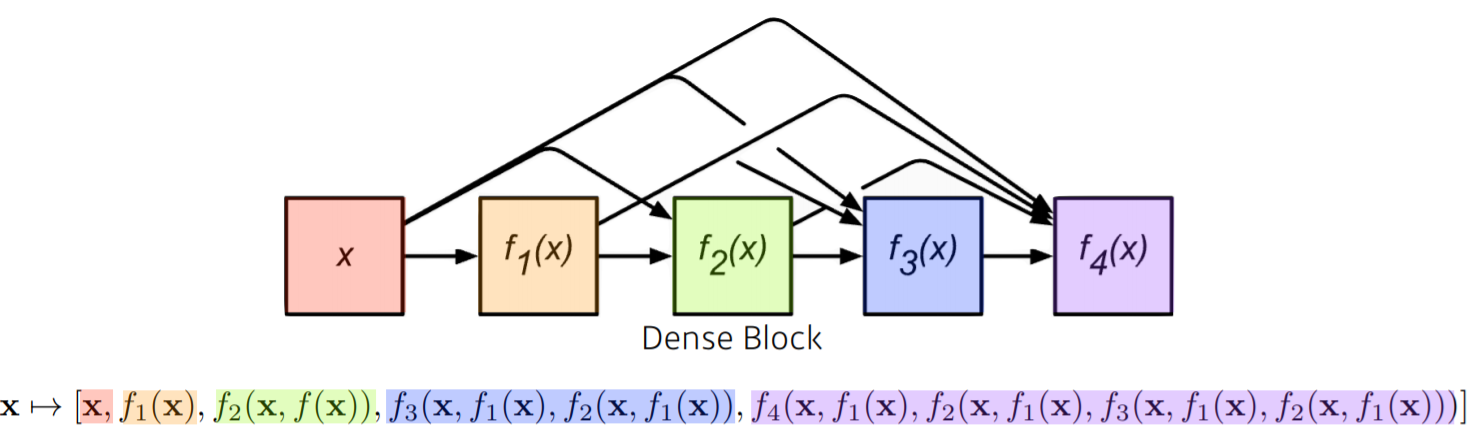
  • ResNet에서는 input을 output에 더해(add)주었다면, DenseNet에서는 input과 output을 합친(concatenate)다. (input과 output의 spatial dimension이 같음) concatenate
  • 하지만 이렇게 하면 channel의 수가 지수단위로 증가(layer를 거칠 때마다 2배로)하고, 그러면 parameter수 역시 급격히 증가할 것이다.
  • 이를 막기 위해 중간중간 1 x 1 convolution으로 channel을 줄여준다. densenet
  • Dense Block에서는 이전 모든 convolution layer의 feature map을 concatenate한다.
  • Transition Block에서는 다른 것도 하지만, 특히 1 x 1 convolution이 들어가 channel 수를 줄인다.
  • 사실 DenseNet은 이해가 아직 잘 안돼서 추후 추가적인 공부가 필요할 것 같다. 지금 당장은 concatenation을 사용했다는 점을 알고 가자.


Computer Vision Application

지금까지 배운 CNN이 Computer Vision 분야에 어떤 식으로 적용되는지 살펴보자.


Semantic Segmentation

semantic_segmentation 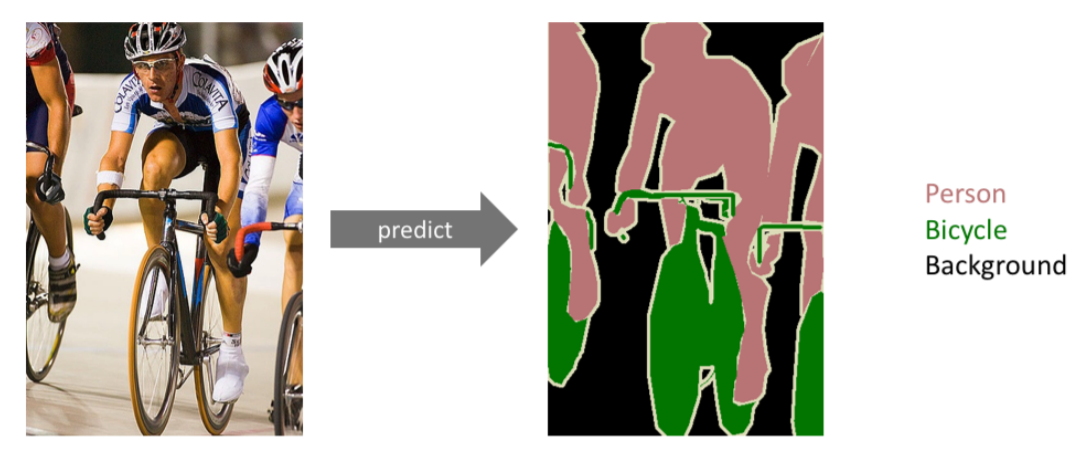semantic segmentation(dense classification)은 위와 같이 이미지를 픽셀 단위로 분류하는 것을 말한다. 흔히 아는 자율 주행에도 이 기술이 들어가게 된다.
이를 구현하기 위해 Fully Convolutional Network(FCN)을 도입하게 된다.

  • Fully Convolutional Network(FCN)
    • 본래 고전 CNN 구조는 맨 뒤에서 affine layer가 들어가게 되면서 후반부에는 output이 flatten되어 각 output의 위치정보가 소실되는 단점이 있었다. FCN
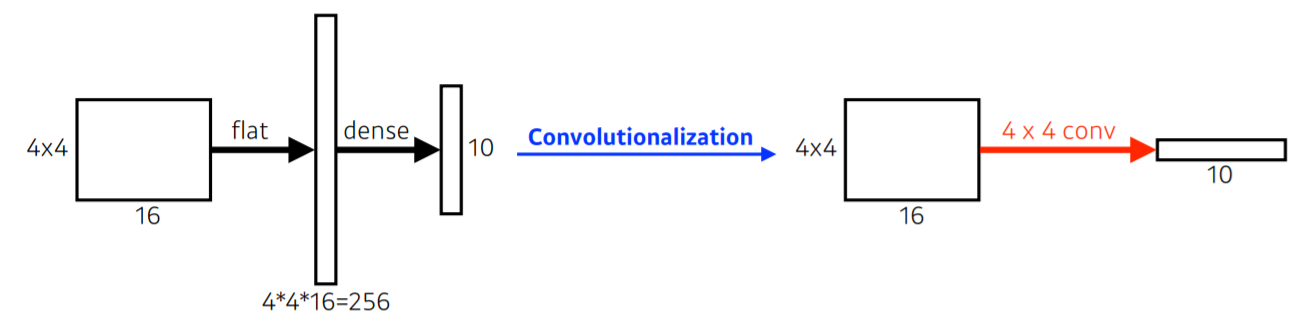
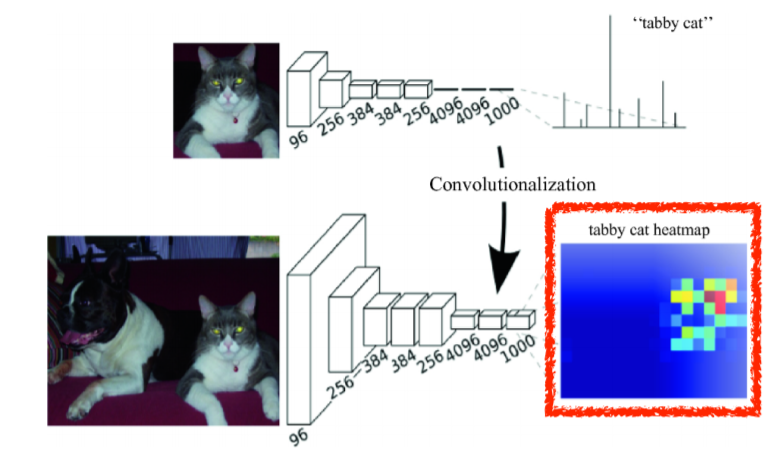
    • FCN에서는 affine layer 대신 1 x 1 kernel을 가진 convolutional layer를 넣어줌으로써 결과적으로 output의 위치정보를 유지할 수 있다. fcn_example
    • 그리고 위치정보를 남길뿐만아니라, input의 size도 자유로워졌다. 본래 affine layer는 input 크기가 딱딱 맞춰들어와야했는데, convolution 연산에서는 거듭 말하지만 커널의 사이즈가 input size와 독립적이기 때문에 어느 입력이든 받아들일 수 있다. 물론, input이 커지면 output도 커지고, input이 작아지면 output도 작아진다. (여기서 말하는 사이즈는 모두 spatial dimension 기준이다)
    • 다만 convolution을 거치면 보통 output의 spatial dimension은 줄어들게된다. 따라서 원본이미지와 크기가 같도록 늘려줄 필요성이 있다.
    • 이를 위해 upsampling(확장), deconvolution(역합성곱)을 해주게되는데, 사실 엄밀히 말하면 convolution의 역연산은 존재할 수 없지만, 맥락이 통하므로 이러한 용어를 사용한다.
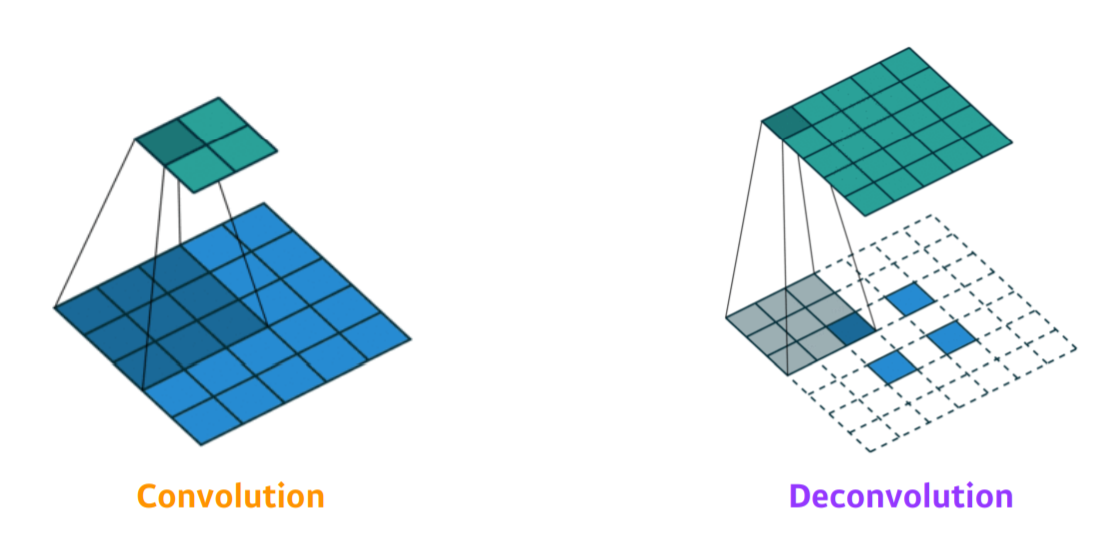
      deconvolution
    • 위와 같이 최종 output에 패딩을 많이 주어서 그것으로 원본 이미지 크기를 만들 수 있는 convolution 연산을 돌리게 되면 이미지를 복원할 수 있다.


Detection

Detection은 픽셀 단위가 아니라, bounding box를 찾는 기법이다. 똑같이 어떤 물체를 찾는데 사용한다.

  • R-CNN
    • R-CNN에 대한 논문에서는 아래와 같은 프로세스를 제시한다.
      1. Input image에서 Selective search라는 알고리즘을 이용해 후보 2000개 box들(regional proposal)을 검출한다. (SS 알고리즘은 다루고자 하는 주제가 아니므로 생략)
      2. CNN(AlexNet)을 통해 각 이미지마다 4096차원의 특성벡터를 도출한다. 단, output의 size를 같게해줘야 하므로 모든 regional proposal의 크기를 정해진 같은 사이즈로 warping해준다.
      3. SVM을 이용하여 해당 박스에 대한 클래스를 예측한다.
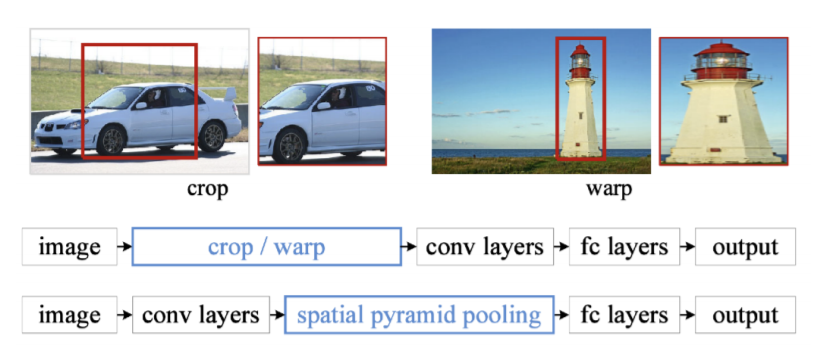
  • SPPNet (Spatial Pyramid Pooling) sppnet
    • R-CNN에서는 후보 2000개에 대하여 모두 CNN을 한 번씩 돌려야했기 때문에 시간이 너무 오래걸렸다.
    • SPPNet에서는 CNN을 한번만 돌린다.
      1. Selective search로 똑같이 후보를 먼저 찾는다.
      2. CNN을 돌려 나온 feature map(output)에서 각각의 bounding box영역의 patch를 뜯어온다. input size를 고정해줄 필요가 없으므로 warp과정이 필요 없다.
      3. SVM을 이용하여 각 박스에 대한 클래스를 예측한다.
    • 위 과정은 매우 축약되어있는데, 사실은 좀더 복잡한 프로세스가 필요하다.
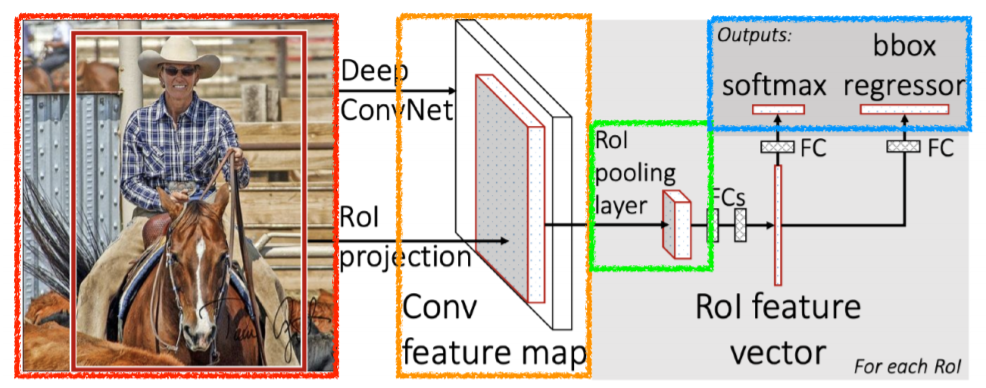
  • Fast R-CNN fastrcn
    • Fast R-CNN은 R-CNN의 단점(2000번의 CNN, 여러 모델에서 학습)을 극복한 기법이다.
      1. Selective search로 regional proposal 추출
      2. CNN을 돌려 feature map을 얻어옴(SPPNet과 여기까지 동일)
      3. 각 region마다 pooling을 진행하며 고정된 크기의 feature vector를 가져옴
      4. feature vector를 affine layer에 통과시켜 두 output(class, bounding box regressor)을 얻는다.
      5. class는 softmax를 통과시켜 분류를 적용하고, bounding box는 bounding box regression을 통해 box의 위치를 조정함으로써 얻는다.
    • 위 과정도 상당히 요약되어있는데, 나중에 자세히 알아보자.
  • Faster R-CNN
    • Selective search 알고리즘 대신 regional proposal까지 학습하여 찾는 Region Proposal Network(RPN)에 Fast R-CNN을 결합한 형태이다.
    • RPN
      • RPN으로는 분류는 하지 않고, 후보들만 찾아낸다(물체의 유무 판단).
      • Anchor box(미리 정해놓은 bounding box의 크기)를 활용하는데, 후보에는 총 9개의 region size가 있으며, 각 region 후보 박스마다 4개의 bounding box regression parameter(w, h, x, y)가 있고, 해당 박스가 정말 쓸모 있는지를 판단하는 box classifier가 2개 있어 RPN에서는 총 9(4 + 2) = 54개의 채널이 필요하다.
  • YOLO
    • YOLO는 현재는 v5까지 나왔으며, 여기서는 고전적인 모델인 v1을 알아보도록 한다.
    • RPN/CNN 등의 과정 없이 이미지를 한번 찍고 바로 여러 bounding box 예측 및 각 클래스에 대한 확률을 구해낸다.
    • 따라서 매우 빠른 속도에 정확도도 높은 성능을 보여준다.
    • 먼저 주어진 이미지를 일정 크기의 grid로 나누는데, 찾고싶은 물체의 중앙이 grid cell에 있으면 그 grid cell의 응답을 통해 bounding과 예측을 동시에 할 수 있다.
    • 각 grid cell은 B개의 bounding box를 예측한다.
      • 각 바운딩 박스는 box refinement(x, y, w, h)와 confidence(정말 물체가 있는가?)를 예측한다.
    • 또한 각 grid cell은 C개의 클래스에 대한 확률값을 예측한다.
    • 결론적으로, 한 이미지에 대하여 $S \times S \times (B \times 5 + C)$ 크기의 tensor를 가진다. ($S \times S$는 그리드의 개수)

이렇게 다양한 Vision 알고리즘들을 알아보았는데, 솔직히 detection 부분은 거의 이해를 하지 못했다 :cry: :cry: :cry: 오늘은 이 많은 알고리즘들을 정말 짧은 시간에 다루었으므로 사실 다 이해가 되지 않는 것은 당연하다. 지금은 대충 어떤 기법을 쓰는지 큰 틀만 기억하고, 각각에 대해서는 나중에 꼭 더 자세히 알아보도록 하자.


Reference

Padding
Local Response Normalization(LRN)
GoogLeNet
ResNet
Fully Convolutional Network(FCN)
Fast R-CNN

← Previous Post Next Post →