Day24. 노드 임베딩, 잠재 벡터

개요

그래프 내 정점을 임베딩하여 벡터로 표현하는 방법과 추천 시스템을 구축할 때 사용할 수 있는 잠재 인수 모형에 대해 알아보도록 한다.

이 글은 아래와 같은 내용으로 구성된다.

• 정점 표현과 노드 임베딩
  • 인접성 기반 접근법
  • 거리/경로/중첩 기반 접근법
  • 임의보행 기반 접근법(DeepWalk, Node2Vec)
  • 손실 함수 근사
  • 변환식 정점 표현 학습과 귀납식 정점 표현 학습
• 잠재 인수 모형
  • 기본적 잠재 인수 모형
  • Additional bias
• Reference

정점 표현과 노드 임베딩

그래프의 정점들을 벡터의 형태로 표현함으로써 벡터 형태의 데이터를 위한 도구들을 그래프에도 적용할 수 있다. Girvan-Newman algorithm 등 이전까지 배운 방법들은 그래프 형태에 특화된 알고리즘이다. 지금까지 거대한 그래프에 대하여 무언가 분석을 하려면 이와 같은 그래프에 특화된 알고리즘을 사용해야했다. 그래프의 각 정점을 임베딩 벡터로 표현하여 이런 특화된 알고리즘을 만들어야하는 수고로움을 덜 수 있다.

노드 임베딩의 기준은 정점간 유사도이다. 이 정점간 유사도를 임베딩 공간에서도 보존 및 표현할 수 있도록 임베딩 벡터를 학습시켜야한다. 이 때, 임베딩 공간에서의 유사도는 내적(inner product)으로 표현된다.

우리의 목표는 그래프에서 각 정점의 유사도와 해당 정점에 대한 두 임베딩 벡터의 유사도가 같게 만드는 것이다. 임베딩 공간에서의 유사도는 위에서 정의했으니, 이제는 그래프에서의 유사도를 정의하기로 한다.

그런데 그래프에서의 유사도는 딱 하나로 정의되지 않는다. 유사도를 정의하는데 있어 여러가지 방법이 있으며, 유사도를 어떻게 정의하느냐에 따라 원하는 task에 대한 실제 성능에 큰 영향을 줄 것이다. 아래에서는 그래프에서의 유사도에 대한 다양한 접근법을 다루어본다.

인접성 기반 접근법

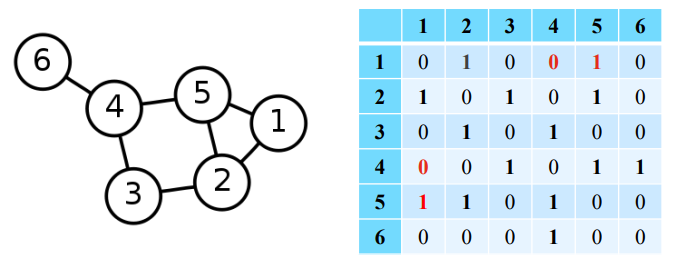
인접성(adjacency) 기반 접근법은 가장 떠올리기 쉬운 방법으로, 두 정점간 직접적으로 연결되는 간선 $(u, v)$의 유무에 따라 그 값이 결정된다. 이를 위와 같이 인접행렬(adjacency matrix)로 나타낼 수 있다. 여기서는 유사도로써 0과 1이라는 두 개의 값만 사용한다.

손실함수는 위와 같이 사용한다. 내적항은 앞서 말했던 임베딩 공간에서의 유사도이고, $A_{u, v}$는 그래프에서의 유사도(인접 행렬의 $u$열 $v$행 성분)이다. 이 둘간의 제곱합(SSE, sum of sqaures)이 손실함수가 되며, 이 손실 함수 최소화를 위해 SGD등을 사용할 수 있다. 최종적으로 학습된 $z_k$항이 $k$번 정점의 임베딩 벡터가 된다.

인접성 기반 접근법은 많은 문제점이 존재한다. 우선 유사도가 반드시 1과 0으로만 나타내어지기 때문에 구체적으로 ‘인접한 정도’를 알 길이 없다. 또한 대다수의 그래프에서 두 정점이 직접 연결되어있지 않아도 같은 군집을 형성하고 있는 경우가 많다.

거리/경로/중첩 기반 접근법

거리 기반 접근법은 두 정점 사이의 거리가 충분히 가까운 경우 유사하다고 간주한다. ‘충분히’의 기준은 hyperparameter인데, 만약 우리가 이것을 2로 설정했다면 거리가 2 이내인 정점쌍은 유사도가 1이 되는 것이다. 반대로 거리가 2보다 큰 정점쌍의 유사도는 0이다. 이는 인접성 기반 접근법을 살짝 확장한 것으로, 똑같이 인접 행렬을 사용할 수 있으며 이에 기반한 손실함수를 같은 형태로 설계할 수 있다.

경로 기반 접근법은 두 정점 사이의 경로가 많을수록 두 정점이 유사하다고 간주한다. 여기서는 경로의 길이를 $k$로 고정시켜놓고 길이 $k$인 경로의 개수를 찾아 이 경로의 수가 많은 두 정점간 유사도가 높다고 가정한다.

만약 $u$와 $v$ 사이의 경로 중 거리가 $k$인 것의 수를 찾고 싶다면 앞서 구한 인접행렬에 $k$제곱을 한 후 $u$열 $v$행 성분을 보면 된다. 즉, 이는 $A^k _{u, v}$라 할 수 있다. 이는 행렬곱의 특성으로 유도해낼 수 있는데 행렬 곱에서는 $(i, j)$ 성분과 $(j, k)$ 성분이 곱해지므로 이 두 경로의 개수의 곱은 $(i, k)$ 경로의 개수라고 할 수 있다. (좀 더 자세한 것은 reference 참조)

따라서 손실함수의 식은 위와 같다.

+++ 실제로는 경로 길이 $k$만을 고려하는 것이 다소 불합리할 수 있다. (홀짝성, $k$보다 짧은 거리 내의 정점은 고려되지 않음 등) 그래서 원래는 해당 term을 $\sum A^k _{u, v}$로 쓰는 것이 맞다. 다만 이것은 요즘은 잘 사용되지 않는 기법으로, 어떤 방식으로 동작하는지만 이해하고 있으면 될 것 같다.

중첩 기반 접근법은 두 정점이 많은 이웃을 공유할수록 유사하다고 간주한다. 즉, 기준이 $S_{u, v} = \vert N(u) \cap N(v) \vert = \sum\limits_{\mathrm{w} \in N(u) \cap N(v)} 1$이 된다.

여기서 $S_{u, v}$항으로 공통 이웃수 대신 자카드 유사도(Jaccard similarity) 혹은 Adamic Adar 점수를 사용할수도 있다.

• 자카드 유사도(Jaccard similarity)는 공통 이웃수의 비율을 본다. $$ S_{u, v} = \dfrac{\vert N(u) \cap N(v) \vert}{\vert N(u) \cup N(v) \vert} $$
• Adamic Adar 점수는 공통 이웃 각각에 가중치를 부여하여 가중합을 계산한다. $$ S_{u, v} = \sum\limits_{\mathrm{w} \in N(u) \cap N(v)} \frac{1}{d_\mathrm{w}} $$

  $d_\mathrm{w}$는 $\mathrm{w}$ 노드의 degree로, degree가 높은 이웃은 $u$와 $v$의 유사도에 큰 영향을 미치지 않는다는 가정 하에 위와 같은 식이 도출된다. 예를 들어, 그런 이웃으로 SNS의 인플루언서가 있을 수 있다. 팔로워 수는 많지만 해당 인플루언서의 팔로워들이 서로 유사성을 띌 확률은 적다.

임의보행 기반 접근법(DeepWalk, Node2Vec)

임의보행(random walk) 기반 접근법은 한 정점에서 시작하여 임의보행을 할 때 다른 정점에 도달할 확률을 유사도로 간주한다. 임의보행 기반 접근법은 시작 정점 주변 지역적 정보와 그래프 전역 정보(거리제한 $k$ 등이 없기 때문)를 모두 고려할 수 있다는 장점이 있다.

임의보행은 세 단계를 거친다.

1) 정점 $u$에서 시작하여 임의보행을 반복 수행
2) 임의보행 중 도달한 정점들의 리스트 $N_R (u)$를 구성, $N_R (u)$에는 당연히 중복된 정점이 있을 수 있다.
3) 손실함수를 최소화하는 임베딩을 학습

이때 손실함수로는 아래와 같은 식을 사용한다.

여기서 $\log(P(v \vert \mathrm{z} _u))$ 항은 $u$에서 시작한 임의보행이 $v$에 도달할 확률을 임베딩으로부터 추정한 결과를 의미한다.

여기서는 앞선 방법들처럼 그래프에서의 유사도를 따로 정의하지 않는데, 사실 이 방법에서 그래프 유사도는 결국 임의 보행 중 도달하는 곳이 된다. 임의 보행을 했는데 도달했다는 것은 거리상으로 어느정도 가깝다는 점을 내포하고있고, 그 중에서도 여러번 도달한 곳은 그 노드로 가는 경로가 많다는 점을 내포하고 있기 때문이다.

따라서 이렇게 임의 보행으로 도달한 정점들에 대하여 유사도를 높여주기 위해 위와 같이 손실함수가 설계된다. 임의보행으로 도달할 수 있었던 곳에 대한 도달 확률을 높이는 것은 곧 분자의 $\mathrm{z}_u ^\intercal \, \mathrm{z}_v$ 항 값을 높이는 작업이 되므로 결국 임베딩 벡터에서 이러한 유사도를 반영하는 작업이 된다.

손실 함수의 값은 최소로 만들어야하는데 지금 하고자 하는 것은 확률을 최대화하는 것이므로 앞에 마이너스를 붙여준다.

앞서 살펴본 방법은 Deepwalk라는 방법으로, 기본적인 임의보행(이웃을 균일한 확률로 선택)을 사용한다.

Node2Vec은 2차 치우친 임의보행(Second-order biased random walk)을 사용한다. 방법은 비슷하지만 직전 정점의 거리를 기준으로 경우를 구분하여 차등적인 확률을 부여하여 임의보행을 수행한다.

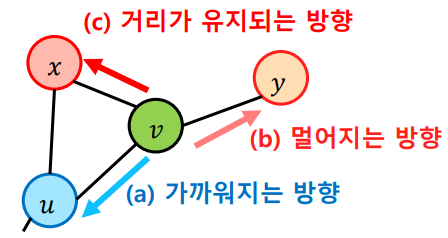
위와 같이 현재 정점($v$)과 직전에 머물렀던 정점($u$)을 모두 고려하여 차등적인 확률을 부여한다.

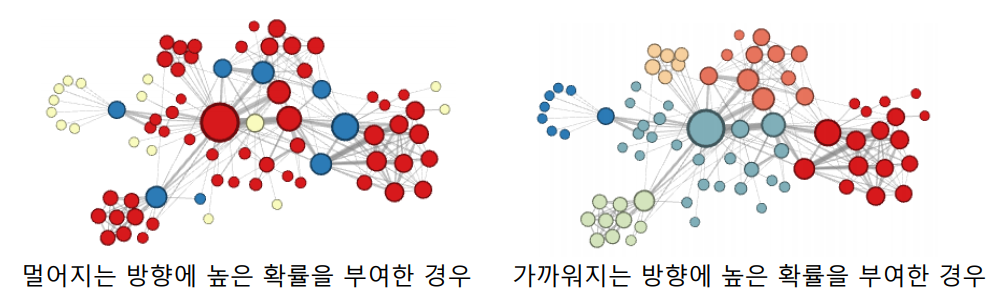
• 멀어지는 방향에 높은 확률을 부여한 경우 정점의 역할(다리 역할, 변두리 정점 등)이 같은 경우 임베딩이 유사하다.
• 가까워지는 방향에 높은 확률을 부여한 경우 같은 군집(community)에 속한 경우 임베딩이 유사하다.

이러한 node2vec기반 노드 임베딩은 Node2Vec 라이브러리의 node2vec() 메소드를 이용하여 수행할 수 있다.

# node2vec.py
import networkx as nx
from node2vec import Node2Vec

... # 전처리 (그래프 생성 등)

node2vec = Node2Vec(G, #networkx 그래프
            dimensions=16, # 임베딩 벡터의 차원수
            walk_length=4, # random walk 한번 당 최대 걷는 길이
            num_walks=200, # node 1개 당 수행하는 random walk 샘플링 횟수
            workers=4 # 쓰레드의 수
            p=1 #가까워지는 방향으로 갈 확률 담당(return)
            q=0.01 #멀어지는 방향으로 갈 확률 담당(inout)
           )
           # p=q=1이면 deepwalk이다.
           # p/(p+q+1)의 확률로 가까워진다.
           # q/(p+q+1)의 확률로 멀어진다.
           # 1/(p+q+1)의 확률로 같은 이웃으로 간다.
model = node2vec.fit(window=2, min_count=1, batch_words=4)
# word2vec처럼 윈도우 사이즈 지정

print(model.wv['2']) #2번 노드의 임베딩 벡터 출력
...

손실 함수 근사

임의보행 기법에서는 손실함수 계산시 정점 집합 $V$에 대한 합이 중첩되어 존재하므로(맨 왼쪽과 확률함수의 분모값) $O(n^2)$의 시간복잡도를 가진다.

따라서 많은 경우 비슷한 역할을 하는 근사식을 사용한다. 모든 정점에 대하여 확률을 정규화하는 대신, 몇 개의 정점을 뽑아서(이렇게 뽑힌 정점을 negative sample이라고 부른다) 이들만을 이용하여 학습할 수 있다.

node2vec 기법은 사실 word2vec과 매우 유사하다. word2vec의 negative sampling에 대해서는 이 글을 참조하도록 하자. word2vec처럼, node2vec도 negative sample을 사용함으로써 매 학습단계마다 한번에 모든 정점의 임베딩을 학습시키지 않고 binary classification(주변 정점인지, 아닌지)으로 중심 정점과 주변 점, 그리고 negative sample의 임베딩 벡터만을 학습시킨다.

손실함수도 기존처럼 전체 정점의 임베딩 벡터의 학습(혹은 전체 정점에 대한 예측)을 위한 형태가 아니라 input으로 들어오는 두 정점의 임베딩 벡터 및 negative sample을 학습시키기 위한 형태로 바뀌게 된다.

여기서는 $k$개의 negative sample, 즉 $k$개의 $u$와 가깝지 않은 sample을 뽑아 대상 정점 $u$와 $v$ 사이의 시그모이드 값(확률 값)이 최대가 되도록 학습시키게 된다. 반대로 대상 정점이 아닌 negative sample 안의 정점들은 $u$와 가깝지 않도록 학습된다.

여기서 이 확률값을 최대화시키는 것은 곧 $u$와 가장 유사도가 높은 정점으로 $v$를 택하겠다는 것과 같다. $u$의 가까이에는 $v$ 말고도 $N_R (u)$ 안의 많은 정점들이 존재한다. 하지만 하고자하는 것은 그 중에서도 $v$와의 유사도가 가장 높도록 만들겠다는 것이다.

만약 단순히 $u$와 $v$의 유사도만을 높이겠다고 하면 뒤에 붙는 마이너스 로그 항은 필요가 없을 것이다. 하지만 $N_R (u)$ 의 정점들 중 negative sample은 거르고 동시에 $v$와의 유사도를 가장 높게 잡겠다라고 했기 때문에 뒷 항이 붙어야 한다. 즉, 뒤에 붙는 부분이 negative sample과의 유사도를 작게 만들어주는 항이다.

negative sample의 의미를 다시 한 번 생각해보면, 결국 $u$와 비슷하지 않은 sample의 집합이다. 우리는 negative sample과의 유사도를 작게 만들고 negative sample이 아닌, window size 내에 있는 정점 $v$와의 유사도를 높게 만들기 위해 식을 위와 같이 설계하였다.

식이 정확하게 저렇게 근사되는 이유에 대해서는 경험적으로 비슷한 결과를 낼 수 있다라는 것이 밝혀졌기 때문인데, 나도 잘은 모르겠지만 아무튼 식의 형태만 봐도 학습이 잘 될 것 같이 생겼다.

결론적으로 위와 같은 식을 사용하여 node2vec의 시간복잡도가 $O(n^2)$에서 $O(nk)$로 바뀌었다. $k$는 아무리 커봐야 random walk의 최대 걸음 수를 넘지 못하기 때문에 시간복잡도를 일차다항시간에 가깝게 줄였다고 볼 수 있다.

변환식 정점 표현 학습과 귀납식 정점 표현 학습

앞서 배운 정점 임베딩 방법들은 변환식(transductive) 방법이다.

변환식 방법은 학습의 결과로 정점의 임베딩 자체를 얻는다는 특성이 있다. 반대로 귀납식(inductive) 방법에서는 정점을 임베딩으로 변화시키는 인코더 함수 $\text{ENC} (v) = \mathrm{z} _v$를 얻을 수 있다.

변환식 임베딩 학습을 적용하면, 학습이 진행된 이후 추가된 정점이 생기면 이에 대한 임베딩을 얻을 수 없다. 또한 모든 정점에 대한 임베딩을 미리 계산하여 저장해두어야하고 정점에 특별한 속성값이 있을 경우 이를 활용할 수 없다.

이러한 다양한 한계점을 극복하기 위해 그래프 신경망(Graph neural network) 기반 귀납식 임베딩 방법이다. 이것에 대해서는 추후 다뤄보도록 한다.

잠재 인수 모형

기본적 잠재 인수 모형

넷플릭스 챌린지(Netflix Challenge)에서 사용된 잠재 인수 모형(Latent factor model)은 사용자와 상품을 모두 벡터로 표현하여 사용자 벡터와 상품 벡터의 유사도가 높으면 사용자에게 해당 상품을 추천한다.

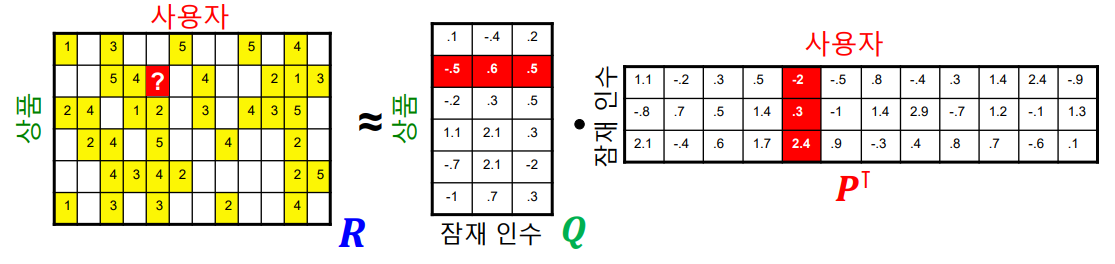
즉, 여기서 하고자하는 것은 사용자 $x$의 임베딩 $p_x$와 상품 $i$의 임베딩 $q_i$, 사용자 $x$의 상품 $i$에 대한 평점 $r_{xi}$에 대하여 $p_x ^{\intercal} \, q_i \approx r_{xi}$가 되도록 학습시키는 것이다.

잠재 인수 모형에서는 아래 손실함수를 최소화하는 행렬 $P$와 $Q$를 찾는 것을 목표로 한다.

집합 $R$은 당연히 훈련 데이터만을 뜻한다.

첫번째 항만 있으면 될 것 같은데 뒤에 또 하나의 항이 붙었다. 이 부분은 모형 복잡도를 나타내는 항으로, 과적합 방지(혹은 regularization)를 위해 붙은 항이다.

이 부분은 L2 regularization, 혹은 weight decay라고도 하는데 이 항이 붙음으로써 가중치가 너무 커지지 않는 방향으로 학습이 진행된다. 이 때, 앞에 붙은 각 $\lambda$항은 learning rate 같은 역할을 하는데, 0에 가까울수록 정규화의 효과가 없어진다. 반대로 너무 크면 가중치가 vanishing 될 수 있다.

학습에서는 기존처럼 손실 함수를 최소화하는 방향으로 SGD 등의 기법을 활용한다.

Additional bias

앞서 상관계수 식을 사용자마다 평점을 주는 기준이 다르다는 점을 고려하여 설계하였다. 잠재 인수 모형에서도 이러한 점이 반영되면 노이즈를 더 줄일 수 있을 것이다.
실제로 사용자의 편향 $b_x$와 상품의 편향 $b_i$, 그리고 이들 모두의 평균 $\mu$를 손실 함수에 반영할 수 있다. 즉, $b_{ui} = \mu + b_x + b_i$라는 편향을 손실함수에 포함시켜 사용자와 상품간 외부 요소를 제외한 순수한 상호작용을 고려할 수 있다.

실제로 잠재 인수 모형의 손실함수로써 아래와 같이 각종 편향을 고려한 형태를 사용할 수 있다.

이렇게 하면 $\mu$를 제외한 다른 평균 값들도 학습의 대상이 되기 때문에 (전체 평균 $\mu$는 그냥 나오는대로 사용하면 됨) 이들에 대한 L2 norm도 regularization을 위해 뒤에 더해지게 된다.

마지막으로 시간적 편향을 고려해볼 수 있다. 어떤 상품의 평점은 시간적 영향을 받을 수 있다. 예를 들어 아래와 같은 영화 평점 그래프를 보자.

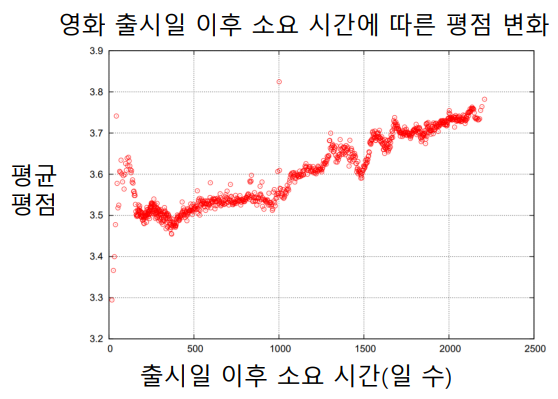
개봉한지 오래된 영화를 굳이 찾아본 배경에는 긍정적 요소가 있을 확률이 높다. (i.e. 좋아하는 배우가 출연, 인기 감독의 작품 등) 따라서 시간이 지남에 따라 영화의 평점이 높아질 가능성이 크다고 생각할 수 있다. (물론 앞선 내용은 예시일 뿐이고 시간의 흐름에 따른 평점이 실제로 어떻게 될지는 실제 데이터를 보아야 알 수 있다) 이 때 시간의 흐름에 따른 사용자 및 상품의 편향 변화를 아래와 같이 생각해볼 수 있다.

사용자가 어떤 상품에 매긴 평점에는 시간에 따른 사용자의 편향 및 상품의 편향, 그리고 사용자와 상품 간 상호작용이라는 여러 요소가 내재되어있다.

지금까지 본 사용자/상품의 임베딩은 surprise 라이브러리의 SVD 클래스를 이용하여 학습시킬 수 있다. 단순히 train data를 주고 학습시킨 후 원하는 uid 및 iid를 넣어 예측값을 얻어올 수 있는 메소드로, 특별한 parameter는 없어 따로 코드를 첨부하지는 않는다.

Reference

Raising an adjacency matrix to a power: Why does it work?
random walks + word2vec