Day25. 그래프 신경망(GNN)

개요

귀납식 임베딩 방법인 그래프 신경망 구조에 대해 알아보도록 한다.

이 글은 아래와 같은 내용으로 구성된다.

• 그래프 신경망
  • 구조 설계
  • 신경망 학습
  • 그래프 합성곱 신경망(GCN), GraphSAGE
  • CNN과 GCN
• GNN with Attention
  • Graph Attentional Layer
  • 그래프 표현 학습과 그래프 풀링
  • Over-smoothing Problem
  • Data Augmentation in GNN
• Reference

그래프 신경망

변환식 임베딩 방법의 단점들을 극복한 귀납식 임베딩 방법에서는 출력으로 임베딩 벡터가 아닌 인코더를 얻는다. 그래프 신경망(GNN)은 대표적인 귀납식 임베딩 방법이다.

구조 설계

그래프 신경망을 이용하면 정점의 속성(feature)을 이용한 임베딩이 가능하다.

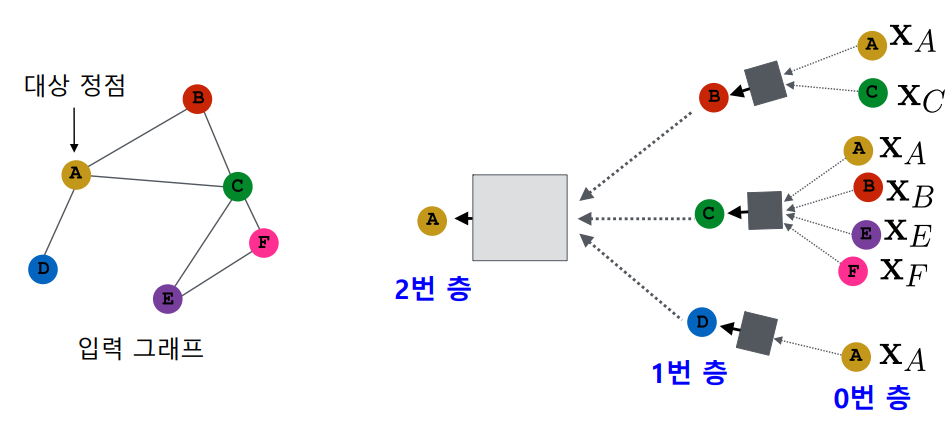
전체적인 구조를 먼저 살펴보면, 위와 같이 목표 정점과 이웃 정점들로 각 layer의 input/output을 구성한다.

어떤 한 layer의 output은 정점의 임베딩이 되는데, 이 정점의 임베딩을 구하기 위해 해당 정점의 이웃들의 정보가 input으로 들어가게 된다. 이때 첫 input($h_0$), 즉 0번층의 input으로써 바로 각 정점의 feature vector를 사용한다.

layer의 개수는 이웃을 몇 단계까지 확장하여 찾을것이냐에 따라 결정된다. 위에서는 target 정점 A의 이웃, 그리고 그 이웃의 이웃까지 총 2개 layer로 신경망을 구성하였다.

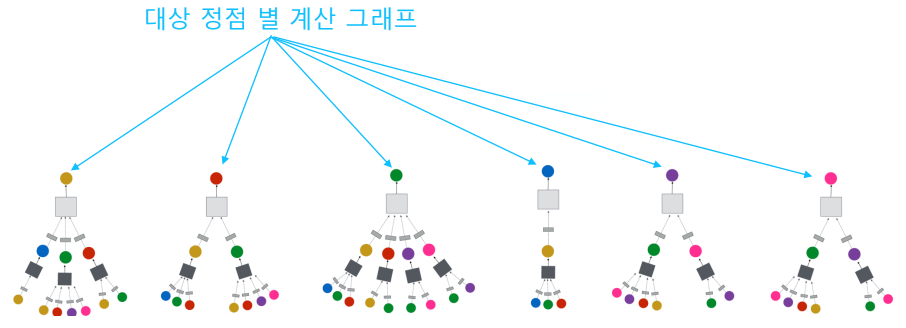
결국 위와 같이 각 정점에 대하여 GNN을 설계하고, 최종 output이 해당 정점의 임베딩 벡터가 된다. 물론 꼭 다 구할 필요는 없고, 임베딩이 필요한 정점들에 대하여서만 신경망을 설계하면 된다. 위와 같이 대상 정점 별 집계되는 구조를 계산 그래프(Computation graph)라고 부른다.

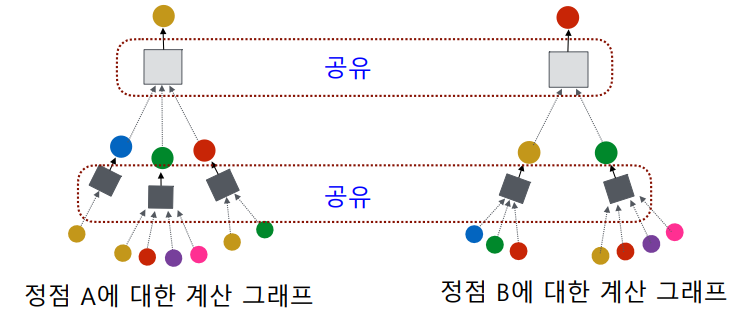
여기서 서로 다른 대상 정점에 대한 임베딩이더라도 층 별 집계 함수는 공유된다. 따라서 새로운 정점이 들어오더라도 무언가 새로 학습시키거나 할 필요 없이 기존에 사용하던 집계 함수를 이용하여 해당 정점의 임베딩을 찾을 수 있다.

그런데 각 정점의 이웃의 수가 다르기 때문에 신경망이 뻗어나가는 가지의 개수가 제각기 다르다. 즉, 입력의 크기가 가변적이다. 따라서 일반적으로는 이웃 정점들로부터 들어오는 input vector의 평균을 구하여 레이어에 통과시킨다.

즉, (1) 이웃들 정보의 평균을 계산하고 (2) 이를 신경망에 적용하는 단계를 거친다.

지금까지 살펴본 것을 위와 같이 식으로 옮겼다. $x_v$는 0번 층에서의 정점 $v$의 임베딩으로, 위에서 언급했듯이 정점 $v$의 속성 벡터로 초기화한다. $h_v ^{(k)}$는 $k$번 층에서 정점 $v$의 임베딩이다. $\sigma$는 ReLU, sigmoid, tanh 등의 활성함수(비선형함수)를 의미한다.

또한 신경망 통과 이전에 이웃들의 정보의 평균을 계산하고 이를 신경망에 통과시키는 항을 볼 수 있다. $B^{(k)}$항은 위에서 언급하지 않았는데, 이 항은 이전 층에서의 정점 $v$의 임베딩 $h_v ^{(k-1)}$을 따로 다른 신경망에 통과시킨다. 그림에는 그려져있지 않지만 사실 target 정점의 임베딩을 구하기 위해 이전 층에서 target 정점의 정보 벡터를 input으로 함께 넣어주어야한다.

최종적으로 $K$번째 layer의 output $z_v$가 우리가 원하는 정점의 임베딩 벡터가 된다.

그래프 신경망에서의 손실함수는 어떻게 설게할 수 있을까? 단순히 설계하면 MSE 등의 손실함수를 사용할 수 있을 것 같은데, 실제로는 downstream task에 기반하여 end-to-end 학습을 할 수 있기 때문에 손실함수의 형태는 downstream task에 의존하는 편이다.

우리의 최종 목표는 그래프의 각 정점에 대한 임베딩이 아니다. 이 임베딩을 활용하여 분류나 군집 탐색, 미래 예측 등을 할텐데 이러한 작업을 수행하는 것이 최종 목표이다.

예를 들어 정점 분류가 최종 목표이면, (1) 임베딩을 얻고 (2) 이 임베딩을 분류기의 입력으로 사용하여 (3) 정점의 유형을 분류한다. 즉, 이런 경우에는 downstream task의 손실함수인 cross-entropy를 GNN의 손실함수로도 사용하는 꼴이 되는 것이다.

여기서 $\theta$는 분류기의 학습 변수이다. 분류기에 임베딩 $\mathrm{z}$을 통과시켜 나온 값으로 binary classification을 행한다고 하면 이에 대한 손실함수를 위와 같이 쓸 수 있을 것이다. 이러한 학습을 종단간(혹은 종단종, End-to-End) 학습이라고 하는데 아래와 같이 학습이 필요한 단들을 분리하지 않고 한꺼번에 학습시키는 것을 말한다.

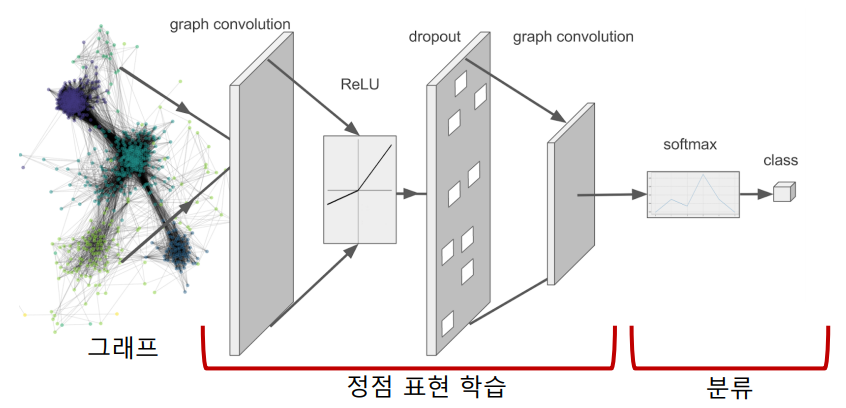
기존에는 변환적 정점 임베딩을 수행한 이후 해당 임베딩을 분류기에 통과시켜 얻은 결과값으로 분류를 수행할 수 있었다. 하지만 이러한 과정을 하나로 통합함으로써 보다 학습이 간편해졌고, 무엇보다도 정확도가 더 높은 것으로 드러났다.

신경망 학습

그렇다면 GNN의 실제 학습은 어떻게 이루어지는지 살펴보자. 이전에 쓴 것과 거의 비슷한 이야기인데, 한 가지 다른 점이 있다면 실제 학습 단계에서 학습을 위해 모든 정점을 이용하지는 않는다. 즉, 학습에 사용할 대상 정점 몇 개만을 정하여 이들만 학습에 이용한다.

물론 validation 및 test를 위해 이렇게 데이터를 분리하는 것도 맞지만, 모델을 데이터 일부만으로 학습시키더라도 encoder의 성능이 어느정도 보장되는 것 같다. 연산해야하는 노드 개수가 적어지니 연산량 면에서도 보다 효율적이다.

최종적으로는 신경망 구조가 으레 그렇듯 backpropagation을 통해 각 가중치를 학습시킨다.

일부 학습 데이터로만 학습시킨 신경망을 통해 학습에 사용되지 않은 정점의 임베딩 역시 얻을 수 있다. 뿐만 아니라 기존에 없었던, 아예 새롭게 추가된 정점의 임베딩도 쉽게 얻을 수 있다. 더 나아가 학습된 그래프 신경망을 아예 다른 그래프(비슷한 정점이나 비슷한 특성을 가진 새로운 그래프)에도 적용해볼 수 있다.

그래프 합성곱 신경망(GCN), GraphSAGE

그래프 신경망에도 여러 종류가 있으며 여기서는 GCN, GraphSAGE에 대해 알아보도록 하자. 모두 input과 output의 형태, 모델의 전체적 구조 등이 비슷하다.

GCN(Graph Convolutional Network)에서는 위에서 살펴본 기본적 GNN구조와 조금 다른 형태의 집계 함수를 활용한다.

여기서는 target 정점에 대한 가중치인 $B^{(k)}$가 없고 이것이 $W^{(k)}$라는 하나의 가중치로 통합되었다. 또한 정규화를 위한 시그마 항의 분모가 변화하였다.

형태에 큰 차이는 없지만, 학습해야하는 가중치의 개수가 줄었고 정규화 방법이 변화하면서 더 빠른 학습 속도 및 성능 향상을 볼 수 있다.

앞서 GNN에서는 입력의 차원이 다르기 때문에 input의 평균을 구한후 이를 신경망에 통과시켜주는 과정을 거쳤다. 실제로는 평균 외에도 여러 aggregate function을 이용할 수 있다.

GraphSAGE는 GCN의 발전된 형태로, 여기서 SAGE는 SAmple과 aggreGatE가 결합된 단어이다. 이것 역시 이전과 거의 비슷한 형태를 띄는데, 평균 외에도 여러 AGG 함수를 골라서 이용할 수 있다는 점, 신경망에 들어갈 때 AGG된 벡터를 자신의 임베딩과 더하는게 아니라 연결(concatenation)한다는 점이 이전과 다른 독특한 특징이다.

AGG 함수로써 평균, 풀링, LSTM 등이 사용될 수 있다.

pool에서의 $\gamma()$는 원소별 최대, LSTM에서의 $\pi()$는 해당 집합을 shuffle한다는 의미이다.

GraphSAGE는 dgl(Deep Graph Library)이라는 패키지를 import하여 그 안의 SAGEConv 모듈을 이용해 구현할 수 있다.

#graphSAGE.py
from dgl.nn.pytorch.conv import SAGEConv
class GraphSAGE(nn.Module):
    '''
        graph               : 학습할 그래프
        inFeatDim           : 데이터의 feature의 차원
        numHiddenDim        : 모델의 hidden 차원
        numClasses          : 예측할 라벨의 경우의 수
        numLayers           : 인풋, 아웃풋 레이어를 제외하고 중간 레이어의 개수
        activationFunction  : 활성화 함수의 종류
        dropoutProb         : 드롭아웃 할 확률
        aggregatorType      : [mean, gcn, pool (for max), lstm]
    '''
    '''
        SAGEConv(inputFeatDim, outputFeatDim, aggregatorType, 
                dropoutProb, activationFunction)와 같은 형식으로 모듈 생성
    '''
    def __init__(self,graph, inFeatDim, numHiddenDim, numClasses, numLayers, 
                            activationFunction, dropoutProb, aggregatorType):
        super(GraphSAGE, self).__init__()
        self.layers = nn.ModuleList()
        self.graph = graph

        # 인풋 레이어
        self.layers.append(SAGEConv(inFeatDim, numHiddenDim, 
                            aggregatorType, dropoutProb, activationFunction))
       
        # 히든 레이어
        for i in range(numLayers):
            self.layers.append(SAGEConv(numHiddenDim, numHiddenDim, 
                            aggregatorType, dropoutProb, activationFunction))
        
        # 출력 레이어
        self.layers.append(SAGEConv(numHiddenDim, numClasses, 
                            aggregatorType, dropoutProb, activation=None))

    def forward(self, features):
        x = features
        for layer in self.layers:
            x = layer(self.graph, x)
        return x

SAGEConv layer는 아래와 같이 직접 구현할 수도 있다. (다만 여기서는 Dropout을 구현하지 않았다) 아래 코드에서는 aggregate function으로 mean을 사용하였다.

#SAGEConv.py
class SAGEConv(nn.Module):
    def __init__(self, in_feats, out_feats, activation):
        super(SAGEConv, self).__init__()
        self._in_feats = in_feats
        self._out_feats = out_feats
        self.activation = activation

        # GraphSAGE에서는 input에 concat된 벡터가 들어가므로 2 * in_feats
        self.W = nn.Linear(in_feats+in_feats, out_feats, bias=True)


    def forward(self, graph, feature):
        # feature을 h에 넣고, h를 m으로 copy하고, neigh에 m의 합이 저장됨
        graph.ndata['h'] = feature
        graph.update_all(fn.copy_src('h', 'm'), fn.sum('m', 'neigh'))

        # Aggregate & Noramlization
        degs = graph.in_degrees().to(feature) #degree(총 개수)
        hkNeigh = graph.ndata['neigh']/degs.unsqueeze(-1) #평균 구하기
        
        # input은 concat되어 들어감.
        hk = self.W(torch.cat((graph.ndata['h'], hkNeigh), dim=-1))

        if self.activation != None:
            hk = self.activation(hk)

        return hk

CNN과 GCN

정점 임베딩에 딥러닝을 적용하라고 하면, 정점들로 만든 adjacency matrix에 CNN을 적용하는 모습을 떠올릴 수 있다.

하지만 이미지 데이터에 CNN을 적용할 때와 달리 그래프에는 인접한 행이나 열간 연관성을 찾기 어렵다. 예를 들어, 이미지의 붙어있는 픽셀은 서로 비슷한 feature를 가질 것이라고 예상할 수 있기 때문에 CNN 구조가 효과적이지만 그래프에서 $i$번째 행과 $i+1$번째 행 사이에 연관성이 있는 경우는 드물다.

이와 같은 맥락에서, 그래프 분석을 위해서는 GCN이라는 별도의 알고리즘을 사용해야한다는 점을 알 수 있다.

사실 지금까지 배운 기본적인 GNN부터 GCN, GraphSAGE에 이르기까지 모두 비슷비슷한 형태를 띄고 있다. 따라서 공통적인 구조에 대해 잘 숙지하고 있는 것이 좋을 것 같다. 더불어 조금의 모델 형태 변화로도 생각보다 큰 성능차이를 불러올 수 있다는 점을 기억하자.

GNN with Attention

GCN에서는 단순히 연결성을 고려한 가중치로 평균을 낸 후 이를 학습에 사용한다.

이 경우 어떤 정점에 대하여 보다 유사도가 높은 정점과 유사도가 낮은 정점을 구별해내지 못한다는 단점이 있다.

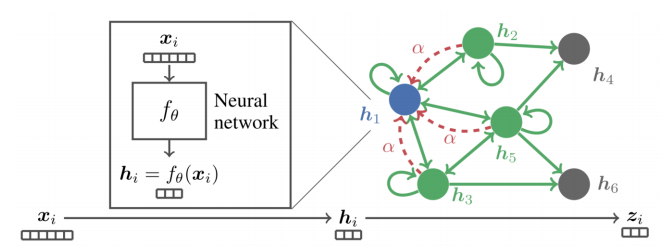
이에 따라 도입된 GAT(Graph ATtention network)에서는 정점 간 유사도를 반영하기 위해 정점 간 가중치(간선 weight)까지 학습시킨다.

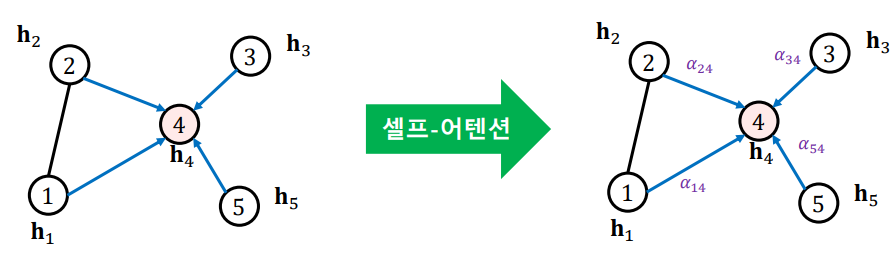
위 그림과 같이 self-attention 기반 신경망을 구성하여 가중치 $\alpha_{ij}$ 또한 학습시킬 수 있게 된다.

GAT에서의 self-attention은 transformer의 그것과는 조금 다르다. 여기서는 정점 임베딩으로 key, query, value 벡터를 따로 뽑아오거나 그런 과정을 거치지 않는다. 다만 transformer에서 모든 input에 대한 연관도를 반영한 새로운 인코딩 벡터를 만들듯이 GAT에서도 모든 정점에 대한 연관도를 반영하여 새로운 인코딩 벡터를 얻는다.

Graph Attentional Layer

그래프 어텐션에는 input으로써 모든 정점의 피처 벡터 집합 $\mathrm{h}$를 넣고 이를 통해 output으로써 새로운 인코딩 피처 벡터 $\mathrm{h} ^{\prime}$을 얻을 수 있다.

$F$는 피처 벡터의 차원, $N$은 정점의 수이다.

그러면 input 단계부터 차근차근 살펴보자.

우리는 먼저 들어온 모든 정점쌍 $(i, j)$의 coefficient($\alpha_{ij}$)를 구해야한다. 그전에 $i$번째 노드에 대한 $j$번째 노드의 중요도(importance) $e_{ij}$를 먼저 구해보자.

이를 위해 (1) $i$번째 정점과 $j$번째 정점에 $F^{\prime} \times F$ shape의 가중치 $\mathrm{W}$를 각각 곱하여 linear transformation을 한 이후 (2) 이 결과를 concat하여 attention mechanism(feedforward neural network) $a$에 투과시켜 최종적으로 importance 값인 $e_{ij}$를 얻을 수 있다.

여기서 $h_i$와 $h_j$는 concat되어 들어가므로, $a$ mechanism 내 linear layer $\vec{a}$의 차원수는 $2F ^{\prime}$일 것이다.

이 때 모든 정점에 대하여 가중치 $\mathrm{W}$와 attention mechanism ${a}$는 공유된다. 따라서 위와 같은 과정을 수행하여 어떤 정점에 대한 모든 이웃 정점의 중요도를 구할 수 있다.

이를 통해 얻은 값을 이용하여 아래와 같은 softmax 함수를 통해 coefficient $\alpha_{ij}$ 값을 구할 수 있다.

$a$는 feedforward neural network로 내부는 weight vector $\vec{a}$와 activation function으로 이루어져있다. 이를 풀어서 쓰면 아래와 같이 쓸 수 있다.

$\Vert$는 concatenation operation을 나타낸다.

원 논문에서는 $a$의 activation function으로 $\alpha = 0.2$인 LeakyReLU를 사용하였다.

이제 이렇게 구한 coefficient $\alpha$ 값을 최종적으로 $\vec{h_i ^{\prime}}$을 구하는데 사용한다.

원논문에서는 여기에 그치지 않고, 학습을 보다 안정화시키기 위해 multi-head attention 구조를 활용한다. 따라서 이에 대한 output으로 $K$개의 인코딩 벡터를 얻게 되는데, 이전에도 그랬듯이 이들을 concat하여 활용할 수 있다.

$\alpha ^{(k)}$와 $\mathrm{W}^{(k)}$는 각각 $k$번째 head에서 계산된 coefficient와 이에 대응하는 $a^k$ attention mechanism의 linear layer이다.

$\alpha$가 head마다 다르다는 점이 뭔가 낯설 수 있는데, GAT에서 attention 구조는 처음 $F$차원 피처 벡터를 $F ^{\prime}$차원으로 linear transformation하는 것부터 시작한다. 따라서 이 과정에서 쓰이는 모든 가중치들과 그 가중치와 연산되어 나온 출력값들은 head마다 다르게 나온다는 점을 잊지 말자.

한편, attention layer를 여러 개 쌓을 경우 네트워크의 마지막 층에서는 위와 같은 concatenation을 하는 것이 거의 무의미하다. 따라서 마지막 layer에서는 concat 대신 averaging을 적용한다. 그리고 마지막 층이므로 downstream task에 따라 activation을 다르게 적용할 수 있을 것이다. 최종 레이어에서의 인코딩은 아래와 같이 나타낼 수 있다.

지금까지 살펴본 GAT의 일련의 동작 과정을 아래 그림과 같이 나타낼 수 있다.

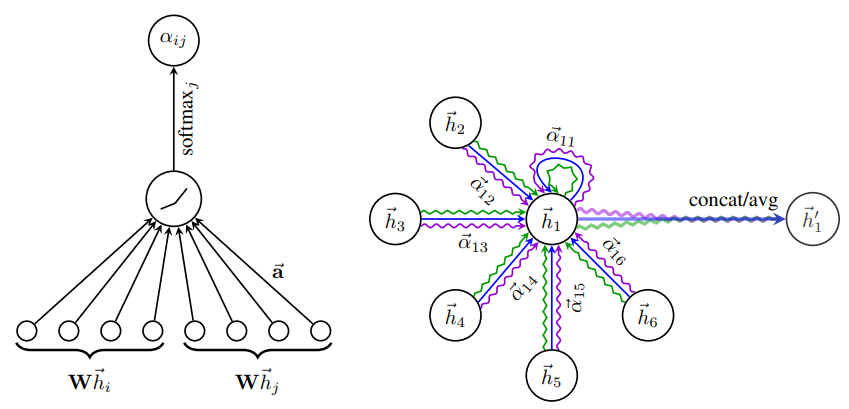
먼저 attention coefficient $\alpha$ 값을 찾기 위해 각 정점쌍의 피처벡터가 $a$ attention mechanism을 통과한다. 이후 이 $\alpha$ 값과 이웃 정점들의 피처 벡터들을 활용하여 최종적으로 target 정점의 인코딩 벡터를 찾는다.

논문에 따르면 이렇게 GAT를 통해 완성된 각 정점의 임베딩을 이용했을 때 정점 분류의 정확도가 기존 모델들에 비해 월등히 향상되었다고 한다. 한편, GAT는 논문에서도 설명이 꽤 쉽게 나와있으므로 보다 자세한 이해를 위해 논문을 한번 읽어보는 것도 좋을 것 같다.

그래프 표현 학습과 그래프 풀링

그래프 표현 학습(혹은 그래프 임베딩)은 그래프 전체를 벡터의 형태로 표현하는 것을 말한다. 이렇게 임베딩된 벡터는 그래프 자체가 어느 클래스에 속하는지 분류하는 문제 등의 그래프 분류 문제에 활용될 수 있다. 이를 위해 Graph2Vec 등의 모델이 존재한다. 이것 역시 word2vec에 상응하는 doc2vec에서 모티브된 모델이라고 볼 수 있을 것 같다. 여기서 따로 Graph2Vec에 대한 기술적 소개는 하지 않는다.

그래프 풀링(Graph pooling)은 정점 임베딩들로부터 그래프 임베딩을 얻는 과정이다. CNN에서의 풀링은 필터 사이즈만큼의 input을 하나로 줄인다. 마찬가지로 그래프 풀링에서도 군집 구조를 띄는 정점 set을 정점 하나(벡터 하나)로 줄인다.

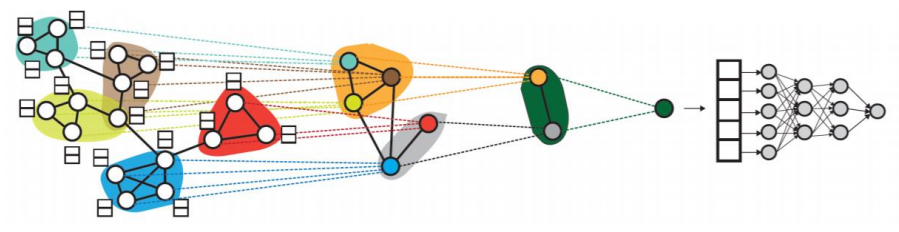
물론 군집을 나누고 해당 군집의 임베딩에 대한 평균을 취하는 등 단순한 방법이 있을 수 있겠지만, 그래프의 구조를 고려한 방법을 사용할 경우 당연히 downstream task에서도 더 높은 성능을 얻을 수 있다. 위 그림과 같이 미분 가능한 풀링(Differentiable pooling, DiffPool)은 군집 구조를 활용하여 임베딩을 계층적으로 집계한다.

이 방법 역시 대충 머릿속으로는 잘 될것 같다는 그림이 그려진다. 다만 마찬가지로 이것까지 다루기에는 너무 복잡하기 때문에 여기서 세세한 부분을 따로 다루지는 않겠다.

Over-smoothing Problem

Over-smoothing(지나친 획일화) 문제란 그래프 신경망의 층수가 증가하면서 정점의 임베딩이 서로 유사해지는 현상을 의미한다.

이는 작은 세상 효과와 관련이 있다. GNN에서 layer 수가 $k$개 일 때, 우리는 거리가 $k$인 정보까지 집계하게되는데, 작은 세상 효과에 따라 $k$가 조금만 커져도 GNN이 그래프 전반을 커버할 수 있게 되어버린다.

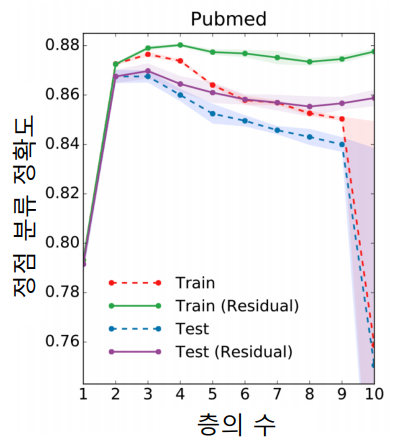
일반적인 GNN은 downstream task에 대하여 위와 같이 layer 수가 2 혹은 3 일때 가장 높은 성능을 보여주고 이후부터는 점점 감소하다가 어느 수준을 넘는 순간 그 성능이 급격히 떨어지는 것을 확인할 수 있다. layer를 10개 이상 쌓으면 그래프 전체를 커버할 확률이 상당히 높아, 성능이 감소하는게 당연해보이기도 한다(…)

이를 방지하기 위해 위와 같이 잔차항(Residual)을 넣는 방법도 고안되었지만 효과가 여전히 제한적이다. 위 그래프에서 residual이 붙은 범례가 residual이 추가된 GNN의 경우이다.

따라서 이에 대한 대응으로 JK network(Jumping Knowledge Network)가 제시되었는데, 여기서는 아래와 같이 마지막 층 임베딩 출력 시 모든 층의 임베딩을 함께 활용한다.

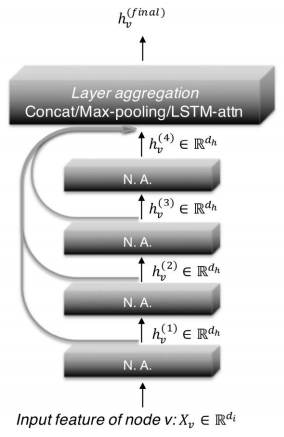
또 다른 대응으로 APPNP가 있는데, 여기서는 0번째 층을 제외하고는 신경망 없이 집계함수를 단순화하였다.

즉, 가중치 $\mathrm{W}$를 0번 layer에서만 곱하고 1번 layer부터는 집계 함수에서 $\mathrm{W}$를 곱하지 않는다. 연구 결과에 따르면 이렇게 처리했을 때는 layer 수 증가에 따른 정확도 감소 효과가 없었다고 한다.

Data Augmentation in GNN

데이터 증강(Data augmentation)은 이전에 컴퓨터 비전 분야에서 이미 한 번 살펴본 바 있다. 데이터 증강을 통해 추가 혹은 보완된 데이터를 통해 모델을 학습시킴으로써 모델의 성능을 더 높일 수 있다.

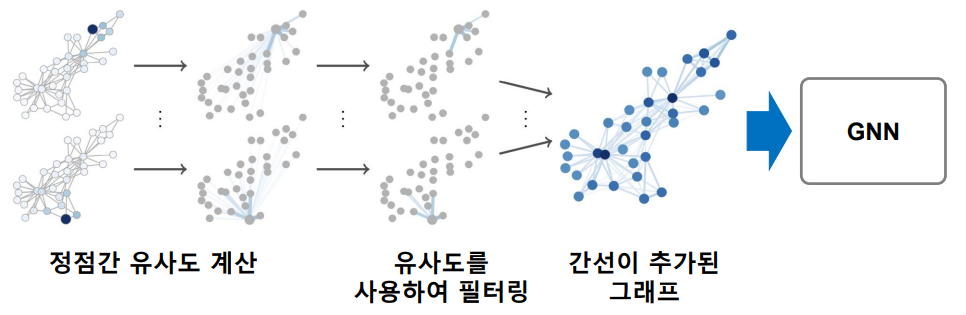
그래프에는 누락되거나 부정확한 간선이 있을 수 있다. 이를 보완하기 위해 먼저 임의보행을 통해 정점간 유사도를 계산한 후 유사도가 높은 정점 간의 간선을 추가하는 방법이 제안되었다. 위 그림은 이러한 과정을 통한 데이터 증강의 예시를 보여준다. 이렇게 생성된 데이터로 GNN을 학습시키면 보다 좋은 성능을 기대할 수 있다.

Reference

Graph Neural Network
GraphSage
Graph Attention Network (GAT) model presented by Veličković et. al (2017)