Day23. 군집 탐색, 추천 시스템

개요

그래프가 주어졌을 때 군집을 어떤 방법으로 인식할 수 있는지에 대해 알아본다. 그리고 협업 필터링을 이용한 기본적인 추천 시스템의 동작 원리에 대해 살펴보도록 한다.

이 글은 아래와 같은 내용으로 구성된다.

• 군집 탐색
  • 군집성(모듈성)
  • 군집 탐색 알고리즘
    • Girvan-Newman algorithm
    • Louvain algorithm
  • 중첩이 있는 군집 탐색
• 추천 시스템
  • 내용 기반 추천시스템
  • 협업 필터링 추천시스템
  • 추천 시스템의 평가
• Reference

군집 탐색

그래프를 여러 군집으로 잘 나누는 문제를 군집 탐색(Community detection) 문제라고 한다. 기계학습에서의 군집화(clustering) 문제와 매우 유사한데 여기서는 피처 벡터의 유사성이 아니라 정점들의 연결성을 기반으로 군집화를 수행한다는 점에 차이가 있다.

군집성(모듈성)

군집화를 수행한 이후, 그래프가 제대로 군집화되었는지 확인하기 위해 군집성(modularity)이라는 지표를 이용한다.

군집성이 무엇인지 알아보기 이전에 배치 모형(configuration model)이 무엇인지 알아보도록 하자.

어떤 그래프의 배치모형은 아래 조건을 만족한다.

1) 각 정점의 연결성(degree)를 보존 2) 간선들을 무작위로 재배치

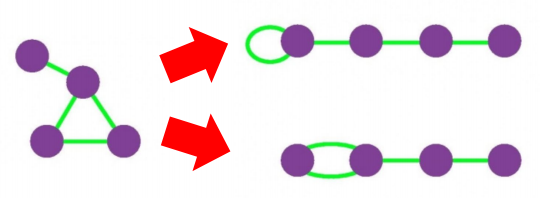
위 그림에서 좌측 그래프는 우측의 두 가지 배치 모형을 가진다. 그래프의 구조는 다르지만(간선이 재배치되었지만) 연결성은 보존된 것을 확인할 수 있다.

배치 모형에서 임의의 두 정점 $i$와 $j$ 사이에 간선이 존재할 확률은 두 정점의 연결성에 비례한다. 배치 모형 하나하나는 모두 확률적으로 생성되기 때문에 degree가 높으면 간선이 생성될 확률이 높다.

이제 군집성을 정의해보면 아래와 같다.

$Q$는 모듈성, $M$은 전체 링크(간선) 수, $a_{ij}$는 $i$와 $j$간 링크 (있으면 1, 없으면 0), $t_{ij}$는 배치 모형에서 $i$와 $j$간 링크 (있으면 1, 없으면 0), $\langle t_{ij} \rangle$은 $t_{ij}$의 기댓값, $C(i)$는 $i$가 속하는 군집(커뮤니티), $\delta \left[ C(i), C(j) \right]$는 $C(i)$와 $C(j)$가 같은 커뮤니티면 1, 다르면 0을 나타낸다.

식에서 볼 수 있듯이, 군집성은 연결성이 같은 타 그래프(즉, 배치 모형)에 비해 얼마나 군집화가 잘 되었는지를 평가하는 지표이다.

군집성의 식을 조금 더 깊게 이해해보기 위해 먼저 $\langle t_{ij} \rangle$의 값을 살펴보자.

$i$와 $j$가 연결된 배치 모형이 나올 확률은 어떤 간선 한쪽 끝에 $i$가 있을 확률 $p_i$와 한쪽 끝에 $j$가 있을 확률 $p_j$의 곱이다. 그런데 $i$와 $j$의 위치가 반전될 수 있으므로 이 확률은 $p_i p_j + p_j p_i$이다. 그런데 현재 간선이 총 $M$개 있으므로 결국 $\langle t_{ij} \rangle$의 값은 아래와 같다.

배치 모형에서는 연결성이 보존된다. 따라서 $p_i$는 $i$ 정점의 연결성과 그래프 모든 정점의 연결성의 합에 대한 비로 나타낼 수 있다. 즉, $i$가 연결되는 간선이 생길 확률은 $i$의 연결성에 비례한다.

$k_l$은 정점 $l$의 degree, N은 정점의 총 개수이다.

모든 정점의 degree($k_l$)를 합하면 $2M$이므로 확률의 합도 1이 되는 것을 확인할 수 있다.

이제 위 식을 처음 군집성 식에 대입하면 아래와 같다.

이 식을 조금 더 단순화하기 위해 $\delta \left[ C(i), C(j) \right]$ 항을 조금 다르게 처리하여 이 식을 아래와 같이 바꿀 수 있다.

$n_C$는 전체 군집(community)의 개수이다.

즉, 어차피 군집이 서로 다른 $i$와 $j$는 계산식에서 상쇄되므로 애초부터 같은 군집에 속하는 $i$, $j$에 대해서만 바라보겠다는 것이다.

우리는 이 식을 조금 더 단순화하기 위해 전체 연결($2M$)에 대한 커뮤니티 간 연결의 비율을 아래와 같이 정의할 수 있다.

$e_{l l ^\prime }$을 이용하여 군집성 $Q$의 식을 아래와 같이 변형할 수 있다.

$i$의 degree는 $i$에 연결된 간선의 합 즉 $k_i = \sum\limits _j a_{ij}$ 이므로

따라서 군집성은

이 식을 행렬에서 처리해보기 위해 다음과 같이 전체 연결 개수 대비 군집 $l$에서 군집 $l^{\prime}$으로의 연결 개수 $e_{ij}$를 아래와 같이 행렬 $\mathrm{E}$로 나타낼 수 있다.

그런데 $e_{ll}$은 같은 군집 $l$ 안에서의 연결의 개수이므로 결국 이는 $\mathrm{E}$의 대각행렬의 합이다.

두번째 항의 경우 $\mathrm{E}$가 대칭행렬(symmetric matrix)이므로

결국 이 값은 행렬 $\mathrm{E} ^2$의 모든 항을 다 더한 값이 된다.

이제 이 두 식을 합치면 아래와 같은 식이 유도된다.

결국 우리는 모든 정점의 각 degree $k_i$를 알아내어 이를 통해 구한 $e_{ij}$로 이루어진 행렬만으로 군집성을 계산할 수 있다.

각 $e_{ij}$는 0과 1사이의 값이기 때문에 군집성 값은 -1과 1 사이의 값을 가진다. 군집성과 모듈성은 같은 의미이나 보통은 모듈성(Modularity)이라고 불리는 것 같으니 두 단어 모두 기억해두도록 하자.

군집 탐색 알고리즘

군집 탐색 알고리즘에는 여러가지가 있지만, 여기서는 대표적인 두 알고리즘 Girvan-Newman 알고리즘과 Louvain 알고리즘에 대해서 알아보도록 한다.

Girvan-Newman algorithm

대표적인 하향식(Top-Down) 군집 탐색 알고리즘이다. 전체 그래프에서 탐색을 시작하여 군집들이 분리되도록 간선을 순차적으로 제거하여 군집성이 최대가 되는 시점의 상태를 결과로 반환한다.

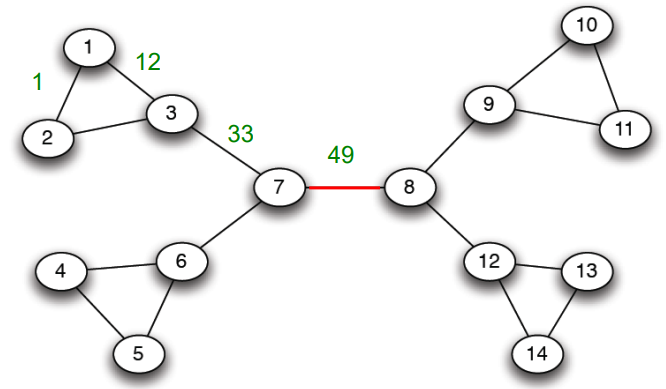
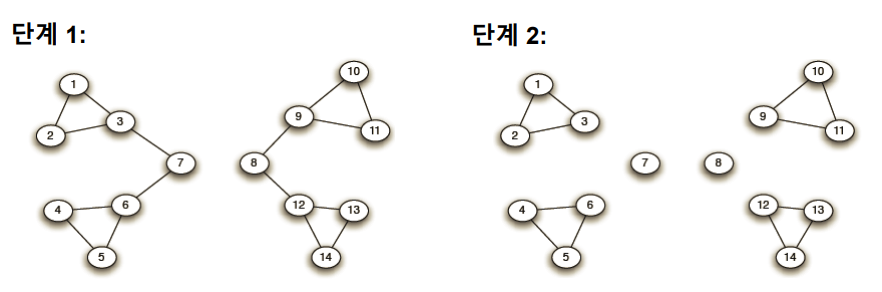
그리고 간선 중 우선 제거 대상을 식별하기 위해 매개 중심성(Betweenness centrality)을 활용한다. 매개 중심성은 어떤 간선이 정점 간의 최단 경로에 놓이는 횟수를 의미한다.

정점 $i$로부터 정점 $j$로의 최단 경로 수를 $\sigma_{i, j}$라고 하고 그 중 간선 $(x, y)$를 포함한 것을 $\sigma_{i, j}(x, y)$라고 하면 간선 $(x, y)$의 매개 중심성은 다음 수식으로 계산된다.

즉, 모든 정점 간 최단 경로에 해당 간선이 포함되는 비율을 구하는 것이다.

간선이 제거될 때마다 최단 경로가 갱신될 수 있으므로 매 iteration마다 매개 중심성은 다시 계산해야 한다는 점을 짚고 넘어가자. 간선이 모두 제거될 때까지 이 작업을 반복하고 앞서 말했듯이 매 iteration마다 군집성을 계산하여 이 값이 최대가 되는 시점의 그래프 상태를 복원한 후 이를 반환한다.

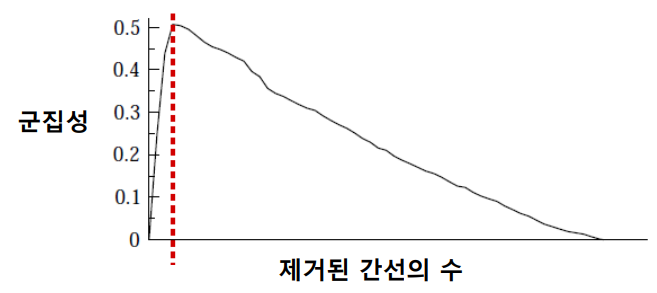
그리고 해당 상태에서 각 연결 요소(connected component)를 하나의 군집으로 간주한다.

실제 코드로는 아래와 같이 구현할 수 있다.

#girvan-newman_algorithm.py
def GirvanNewmanAlgorithm(G, nodeColorList):

    copyG = G.copy() # 기존 그래프를 복사
    pos = nx.spring_layout(copyG)

    """ 초기화 """
    maxModCom = [] # modularity가 최대일 때의 커뮤니티의 정보들을 저장
    maxMod = -1    # modularity가 최대일 때 값 기록 (-1 < Q < 1)

    """ Girvan-Newman algorithm """
    while len(copyG.edges()) > 0:   # 모든 엣지가 사라질때까지 진행한다. 
        # 현재 그래프에 존재하는 커뮤니티 [{Com1}, {Com2}, ... ]
        recComList = sorted(
                            nx.connected_components(copyG), 
                            key=len, 
                            reverse=True
                     )
        
        # 추출된 커뮤니티의 modularity 계산 
        recMod = community.modularity(G, communities=recComList)
        
        if recMod > maxMod: 
            maxModG = copyG.copy()
            maxMod = recMod
            maxModCom = []
            for j in range(len(recComList)):
                maxModCom = maxModCom + [recComList[j]]
            maxStep = step

        """ remove edge """
        step = step + 1

        # betweennes centrality 계산
        betweenness = nx.edge_betweenness_centrality(copyG) 
        maxEdge = max(betweenness, key=betweenness.get) 
        copyG.remove_edge(maxEdge[0], maxEdge[1])

    return maxModG, maxMod, maxModCom

NetworkX에서는 Girvan-Newman 알고리즘 기반 군집 분석을 위한 메소드로서 networkx.algorithms.community.girvan_newman() 메소드를 제공하고 있다.

Louvain algorithm

대표적인 상향식(Bottom-Up) 군집 탐색 알고리즘이다. 앞서 Girvan-Newman 알고리즘과 반대로 개별 정점에서 시작하여 점점 큰 군집을 형성한다. 즉, 처음에는 정점 하나하나가 하나의 군집을 형성하며 알고리즘을 수행할수록 그 군집들이 서로 합쳐지면서 더 큰 군집을 형성해나간다.

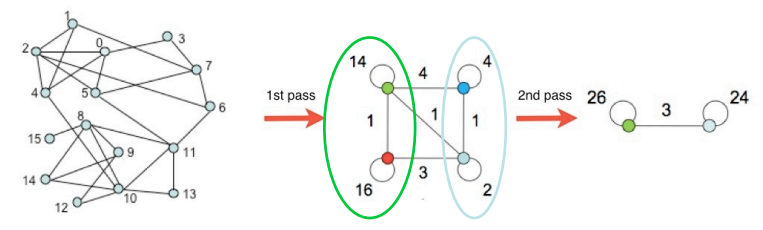
여기서도 군집성을 평가 지표로 활용하여 군집을 합친다. 구체적으로는, 정점이 속한 군집을 인접한 다른 군집으로 재배치하였을 때의 군집성 변화를 측정한다.

앞서 살펴본 군집성에 대한 식을 특정 군집 $C_l$에서만 살펴본다면 아래와 같이 쓸 수 있다.

그러면 군집성의 변화는 아래와 같다.

(군집성의 변화량) = ($i$가 배속됐을 때의 변화량) - ($i$가 배속되지 않았을 때의 변화량)

참고로 두번째 항에서 $\left( \frac{k_i}{2M} \right) ^2$이 붙는 이유는 군집성의 변화를 측정할 때 이전 상태로써 정점 $i$를 기존 군집에서 빼낸 상태를 사용하기 때문이다.

아래 그림을 보면 이 식을 좀 더 명확히 이해할 수 있다.

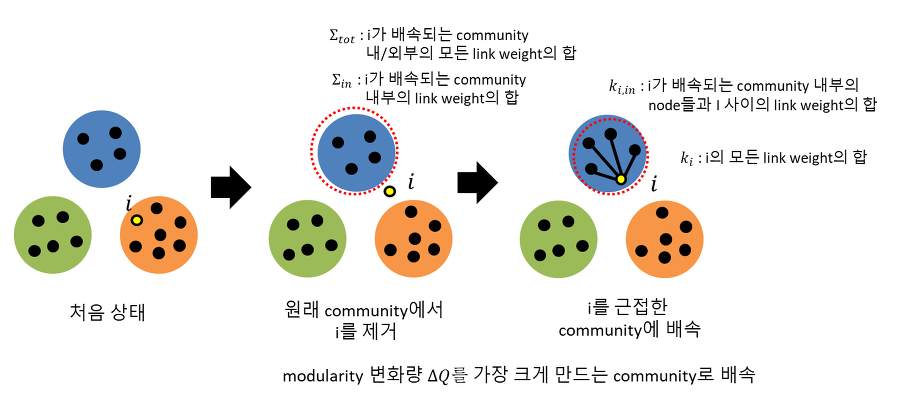
Reference 블로그의 Louvain algorithm 포스트 中

최종적으로 변화량이 가장 큰 군집에 $i$ 정점을 배속시킨다. 이를 변화가 일어나지 않을 때까지 반복한다.

그런데 이 방법은 어떤 정점부터 배속시키기 시작할 것이냐에 따라 계산 결과가 달라질 수 있다. 이것도 일종의 greedy algorithm의 맥락에서 이해할 수 있는 알고리즘이기 때문이다.

하지만 논문의 저자는 실험적으로 이러한 배속 순서가 modularity에 큰 영향을 주지 않는다는 점을 밝혀냈다. 그러나 이러한 순서가 연산 속도에는 영향을 미칠 수 있다고 한다.

이렇게 모든 정점을 어떤 군집에 배속시킨 후 해당 군집을 하나의 정점으로 합친다.

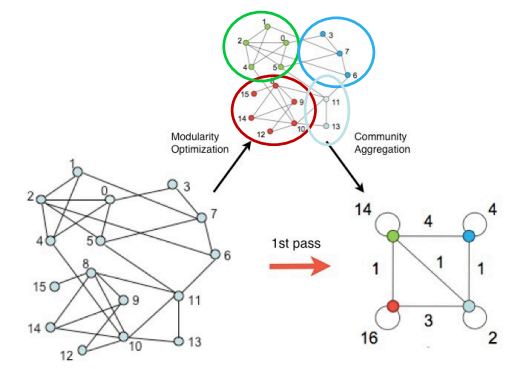
이후 합쳐진 정점들은 앞선 과정을 통해 다시 군집화를 수행하고 최종적으로 더이상 군집성이 증가하지 않을 때(즉, 군집성의 변화량이 0일 때) 알고리즘을 종료한다. 군집성이 증가하지 않는다면 각 연결요소가 모두 하나의 정점으로 aggregation된 상황일 것이다.

중첩이 있는 군집 탐색

위에서 살펴본 알고리즘들은 모두 군집 간 중첩이 없다는 가정 하에 동작한다.

하지만 현실 세계에서는 한 명의 사람이 여러 사회적 관계를 맺고 있을 것이기 때문에 이는 현실세계와는 조금 동떨어진 면이 있다.

중첩이 있는 군집을 탐색하기 위해 새로 중첩 군집 모형을 가정한다. 중첩 군집 모형은 아래와 같은 조건을 만족한다.

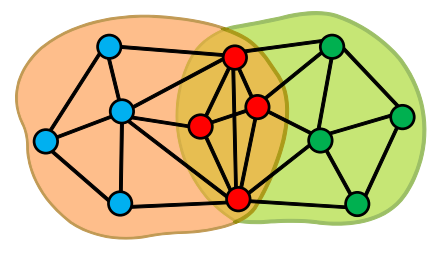
1) 각 정점은 여러 군집에 속할 수 있다.
2) 각 군집 $A$에 대하여 같은 군집에 속하는 두 정점은 $p_A$의 확률로 간선으로 직접 연결된다.
3) 두 정점이 여러 군집에 동시에 속할 경우 간선 연결 확률은 독립적이다; 두 정점이 모두 군집 $A$, $B$에 동시에 속할 경우 두 정점이 연결될 확률은 $1 - (1-p_A)(1-p_B)$이다. ($A$에서도, $B$에서도 연결되지 않는 사건의 여사건 확률)
4) 어느 군집에도 함께 속하지 않은 두 정점은 낮은 확률 $\epsilon$으로 직접 연결된다.

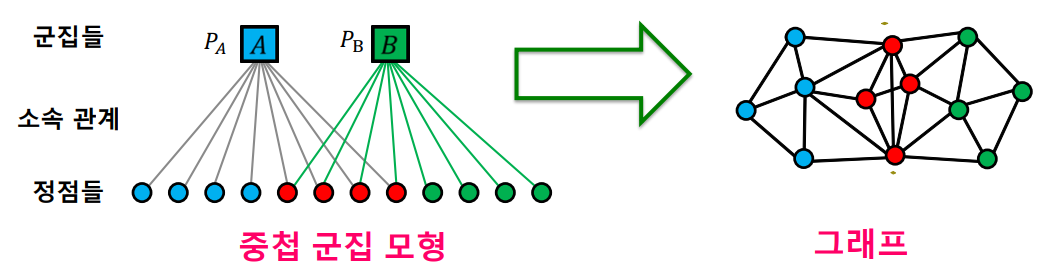
이 모형을 통해 각 정점들이 연결될 확률을 알 수 있으므로 어떤 그래프가 형성될 확률 역시 구할 수 있다.

그런데 우리가 하고자 하는 것은, 모형으로부터 그래프를 찾아내는게 아니라 그래프로부터 모형을 찾아내는 것이다.

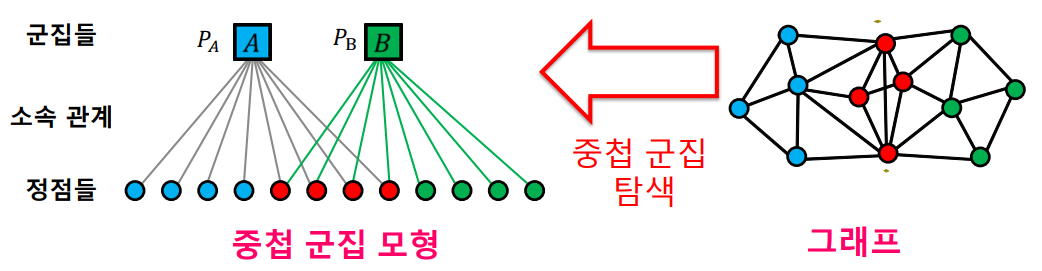
즉, 중첩 군집 탐색은 그래프의 확률을 최대화하는 중첩 군집 모형을 찾는 과정이다.

이는 결국 그래프의 확률에 대한 최우도 추정치(maximum likelihood estimate)를 찾는 것과 동일하다.

그런데 문제는, 군집모형에서 각 정점은 ‘이 군집에 속한다/속하지 않는다’라는 이산적인 변수로서 군집화되기 때문에 이를 최적화하기 위해 (continuous에서만 동작하는)경사하강법 등의 기법을 사용하지 못한다는 것이다.

따라서 이를 사용할 수 있게 하기 위해 완화된 중첩 군집 모형을 활용한다.

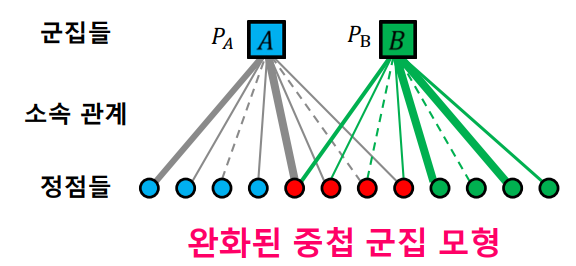
완화된 중첩 군집 모형에서는 이산적인(혹은 binomial) 변수를 사용하지 않고 실수값으로 군집에 대한 소속 정도를 표현한다.

위 그림에서는 각 군집과 정점이 연결되는 선의 굵기가 다른데, 이것이 바로 그 소속 정도(소속감)를 나타낸다. 즉, 기존 모형과 달리 여기서는 속하거나 속하지 않는 이 중간의 단계를 표현할 수 있는 것이다.

최적화 관점에서는 모형의 매개변수들이 실수값을 가지기 때문에 앞서 말한 경사하강법 등의 익숙한 최적화 도구를 사용하여 모형을 탐색할 수 있다는 장점이 있다.

한편, 실제 세계에서도 우리가 여러 사회적 집단에 속하더라도 각 집단에 느끼는 소속감이 모두 다르기 때문에 이 또한 현실 세계를 보다 섬세하게 반영한 점이라고 볼 수 있다.

추천 시스템

추천 시스템은 사용자 각각이 선택할 만한(구매할 만한) 혹은 선호할 만한 상품을 추천한다.

여기서 구매 기록이라는 암시적(implicit) 선호만 있을 수도 있고 명시적(explicit) 선호가 있는 경우도 있다. 추천 시스템의 최종 목표는 어떤 경우가 주어지더라도 해당 상황에 최적화된 방법을 통해 사용자에게 아이템을 추천하는 것이다.

추천 시스템은 그래프의 관점에서 보면 미래의 간선을 예측하는 문제(구매 예측) 혹은 누락된 간선의 가중치를 추정하는 문제(평점 예측)로 해석할 수 있다.

내용 기반 추천시스템

내용 기반(content-based) 추천은 각 사용자가 구매/만족했던 상품과 유사한 것을 추천하는 방법이다.
이는 단순히 개인별 구매 상품 내역에 기반하여 상품을 추천하기 때문에, 타 사용자의 데이터가 필요 없다.

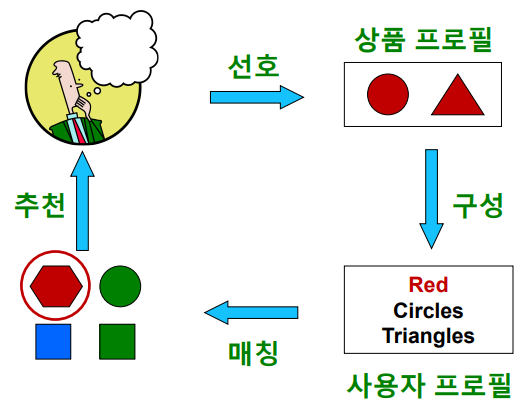
내용 기반 추천은 위와 같은 과정을 통해 사용자에게 상품을 추천한다.

먼저 상품별로 상품의 특성을 담은 임베딩 벡터를 만든다. 여기서 이 임베딩 벡터는 원-핫 인코딩 기반으로도 만들 수 있는데, 상품의 각 피처를 하나의 원-핫 벡터로 나타내는 것이다. 이를 통해 만든 임베딩 벡터는 예를 들어 빨간색+원모양 상품을 $\scriptstyle [ 1, 1, 0, \cdots ]$로 나타내고 빨간색+삼각형 상품을 $\scriptstyle [ 1, 0, 1, \cdots ]$로 나타낼 수 있다. 이 경우 첫번째, 두번째, 세번째 entry는 각각 ‘빨간색’, ‘원’, ‘삼각형’이라는 특성을 나타낸다.

다음으로 대상 사용자의 프로필 벡터를 구성한다. 이것은 사용자의 선호도를 기반으로 상품 벡터에 가중 평균을 취하여 구할 수 있다. 예를 들어 사용자가 빨간 원 상품에 별점 4/5점, 빨간 삼각형 상품에 별점 1/5점을 줬고 이 두 물품만 구매했다면 가중 평균을 통해 $\scriptstyle [ 1, 0.8, 0.2 ]$라는 사용자 프로필 벡터를 얻을 수 있다.

마지막으로 이 사용자 프로필 벡터와 사용자가 구매하지 않은 상품들에 대하여 코사인 유사도를 계산한다. 코사인 유사도는 앞선 포스트에서도 살펴봤듯이 아래와 같이 나타내어진다.

최종적으로 코사인 유사도가 높은 상위 상품들을 사용자에게 추천하게 된다.

내용 기반 추천 시스템은 위에서 보았듯이 다른 사용자의 구매 기록이 필요하지 않고 독특한 취향의 사용자에게도 적절한 추천 상품을 제시할 수 있다. 또한 상품 특성만 알고 있다면 새로운 상품도 추천할 수 있다. 그리고 추천의 근거를 명확히 제시할 수 있다.

반면 상품 특성(상품에 대한 부가 정보)을 모른다면 어떠한 상품도 추천이 불가능하며, 구매 기록이 전혀 없는 사용자에게는 추천해줄 수 있는 상품이 없다. 또한 과적합(overfitting)으로 지나치게 협소한 추천을 할 위험이 있다. 만약 사용자가 우연히 비슷한 특성을 가진 상품을 여러 개 구매했을 경우 전혀 예상치 못한 상품이 제시될 수도 있다.

협업 필터링 추천시스템

협업 필터링(collaborative filtering)은 주로 사용자-사용자간 협업 필터링을 사용한다. 여기서는 대상 사용자와 유사한 취향의 사용자들이 선호한 상품을 추천한다.

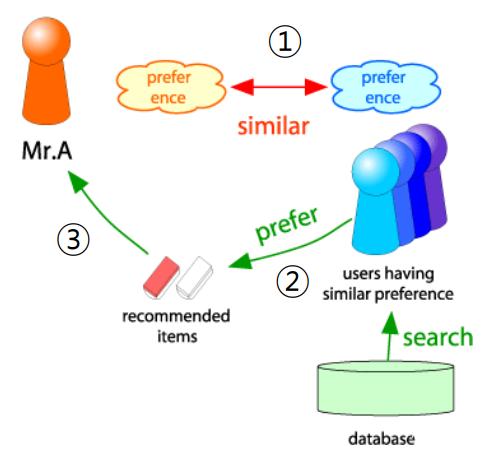
여기서 취향의 유사도는 상관 계수(correlation coefficient)를 통해 측정된다. (여기서 다루는 상관 계수는 Pearson 상관계수이다) 상관계수 식은 아래와 같다.

사용자 $x$가 상품 $s$에 매긴 평점을 $r_{xs}$, 사용자 $x$가 매긴 평균 평점을 $\bar{r_x}$, 사용자 $x$, $y$가 공동 구매한 상품들의 집합을 $S_{xy}$라 한다.

만약 $x$와 $y$의 취향이 비슷하다면, 분자에서 곱해지는 두 항이 둘 다 양수 혹은 둘 다 음수라서 결과적으로 더해지는 값이 양수가 될 것이다. 반대로 취향이 다르면 $x$가 선호하는 상품을 $y$가 비선호하거나 혹은 반대일 것이다. 이 경우 더해지는 값이 음수가 될 것이다. 결과적으로 상관계수 값이 높을수록 두 사람의 취향이 비슷하다고 할 수 있다. 참고로, 이같은 특성을 가지는 상관계수 식의 분모는 공분산(covariance)으로, 두 변수가 같은 방향으로 움직이는 정도를 측정한다.

분모에서는 공분산을 각각의 표준편차로 나누어준다. 이는 측정단위와 관계 없이 두 변수간의 연관성 경향을 나타내주기 위한 작업이다. 사람마다 평점을 짜게 주는 사람이 있을 수 있고 평점을 후하게 주는 사람이 있을 수 있는데 이러한 문제를 여기서 보정해준다. 이는 일종의 정규화 작업으로, 이 작업으로 인해 상관계수는 반드시 -1에서 1까지의 값을 갖는다.

상관 계수, 즉 취향의 유사도를 가중치로 사용한 평점의 가중평균을 통해 어떤 사용자가 구매하지 않은 상품에 대한 평점을 추정할 수 있다.

예를 들어 사용자 $x$가 구매하지 않은 상품 $s$에 대한 평점 $r_{xs}$를 추정하는 경우를 생각해보자. 먼저 상관계수를 이용하여 상품 $s$를 구매한 사람 중 $x$와의 상관계수가 높은 $k$명의 사용자 $N(x;s)$를 뽑는다.

그러면 $x$의 $s$에 대한 예상 평점 $\hat{r}_{xs}$는 아래와 같이 추정할 수 있다.

결론적으로 시스템은 $\hat{r}_{xs}$의 값이 가장 높은 상위 상품들을 $x$에게 추천하게 된다.

협업 필터링은 상품에 대한 부가 정보가 없는 경우에도 사용할 수 있지만, 충분한 평점 데이터가 누적되어야 정확한 추천이 가능하다는 단점이 있다. 또한 새 상품이나 새 사용자에 대한 추천이 불가능하고 독특한 취향의 사용자는 비슷한 취향의 사람이 적어 적절한 추천을 할 수 없다는 문제점도 있다.

추천 시스템의 평가

위에서 사용한 협업 필터링 추천 시스템의 경우 test data를 설정한 후 해당 test 상품들에 대한 사용자의 평점을 알고리즘을 통해 예측할 수 있다. 이후 평균제곱오차(MSE) 혹은 평균제곱근오차(RMSE)를 통해 오차를 측정할 수 있다.

이 밖에도 평가를 위해 여러가지 방법을 사용해볼 수 있다.

• 추정한 평점으로 순위를 매긴 후, 실제 평점으로 매긴 순위와의 상관 계수를 계산
• 추천한 상품 중 실제로 구매로 이루어진 것의 비율 측정
• 추천의 순서 혹은 다양성까지 고려하는 지표

어떤 알고리즘을 사용하든, 이에 대한 성능 평가는 필수적이다. 추천 시스템이 추구하는 방향에 따라 적절한 평가 지표를 활용해야할 것이다.

Reference

Network Modularity (네트워크의 모듈성)
Louvain algorithm