개요
검색엔진에서 많이 사용되는 pagerank 알고리즘에 대해 알아본다. 이후 바이럴 마케팅을 위한 전파 모형 및 전파 최대화를 위한 시드 집합을 찾는 방법에 대해 알아보도록 한다.
이 글은 아래와 같은 내용으로 구성된다.
PageRank
웹은 웹페이지와 하이퍼링크로 구성된 거대한 방향성 있는 그래프이다.
각 웹페이지는 정점에 해당하며 웹페이지가 포함하는 하이퍼링크는 해당 웹페이지에서 나가는 간선에 해당한다.
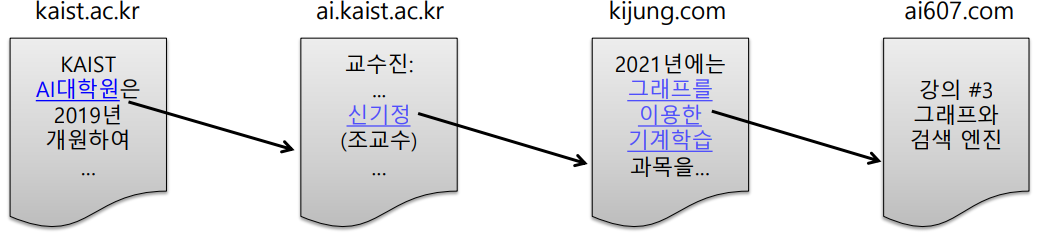
과거에는 웹을 디렉토리화하여 토픽별로 분류하거나, 검색한 키워드가 가장 많이 등장한 페이지를 띄우는 방식의 검색엔진을 활용하였으나
웹의 크기가 커지고 한편으로는 이러한 검색엔진을 속일 수 있는 다양한 악의적 웹페이지들이 등장하면서 새로운 검색엔진의 필요성이 대두되었다.
구글의 Pagerank 알고리즘은 투표 기반의 검색 방법을 활용한다. 투표는 웹페이지가 직접 하게 되며, 해당 웹페이지에서 뻗어나가는 간선 하나하나가 도착 정점으로의 투표로 간주된다. 예를 들어 웹페이지 $u$가 $v$로의 하이퍼링크를 포함하면 $u$가 $v$에게 투표를 했다고 간주하는 것이다.
이에 따르면 간선이 많을수록 많은 표를 받게 되는데, 이 또한 악용 우려가 있기 때문에 관련성이 높고 신뢰할 수 있는 웹사이트의 투표를 더 중요하게 간주하는 가중 투표를 한다.
페이지랭크의 아이디어
앞에서는 투표를 한다고 하였지만, 이를 조금 다른 관점에서 확률 분포로 해석할 수 있다. 즉, 어떤 웹서퍼가 시간 $t$가 흐를 때마다 어떤 웹사이트로 임의 보행(random walk)을 한다고 할 때 어떤 페이지 $j$로의 접근 확률을 구할 수 있다.
웹서퍼가 시간 $t$에 방문한 웹페이지가 웹페이지 $i$일 확률을 $p_i(t)$라고 하자. 이는 $i$ 뿐만 아니라 모든 정점에 대하여 정의할 수 있으므로 결국 모든 웹페이지에 대하여 시간 $t$에 방문할 확률을 나타낸 길이 $\vert V \vert$인 확률분포 벡터 $p(t)$ 또한 정의할 수 있다.
확률은 간단하고 직관적인 방법으로 계산된다. 출발 정점 $i$에서 $N_{out}(i)$에 있는 어떤 정점으로 갈 확률은 ${1 \over N_{out}}$으로 균일하다고 가정한다. 그러면 $t$ 시점에 정점 $i$에 있을 확률이 $p_i(t)$이므로 $t+1$시점에 $j$에 있을 확률은 아래와 같다.
$d_{out}(i)$는 out degree를 나타낸다.
이는 단순히 위에서 서술한 두 확률 값을 곱한 값으로 쉽게 이해할 수 있다.
그런데 우리가 구하고 싶은 것은 어떤 시점에서의 확률값이 아닌, 보다 일반화된 확률값이다. 웹서퍼가 웹서핑을 무한히 반복한다고 하면, 즉 ${t \to \infty}$이면 확률분포 $p(t)$는 수렴하게된다.
즉, $p(t) = p(t+1) = p$가 성립하므로 수렴한 확률 분포 $p$는 아래와 같이 나타낼 수 있다.
이렇게 어떤 값에 수렴하는 확률 분포를 stationary distribution(정상 분포)라고 부른다.
이를 확률분포가 아닌 투표 관점으로 해석한다고 하면 $p_i$를 확률이 아닌 어떤 점수 값 $r_i$로 보고 자신의 점수를 $N_{out}(i)$ 들에게 균일하게 나눠준다고 볼 수 있는데, 이 때 아래와 같은 식이 나오게 된다.
물론 그 형태는 완전히 동일하다.
페이지랭크의 계산
페이지랭크 점수 계산은 반복곱(Power iteration)을 활용한다.
1) 모든 웹페이지에 대하여 그 점수를 ${1 \over \vert V \vert}$로 초기화한다. 즉, 어떤 웹페이지 $i$의 초기 점수는 반드시 $r _i ^{(0)} = {1 \over \vert V \vert}$이다.
2) 위에서 본 시간 $t$에 대한 식을 기반으로 iteration을 돌면서 페이지랭크 점수를 갱신한다.
3) 갱신을 하다가 페이지랭크의 점수가 수렴($r ^{(t)} \approx r ^{(t+1)}$)하면 알고리즘을 종료한다.
그런데 현재의 식으로만 알고리즘을 돌리면 몇 가지 문제가 발생한다.
- 스파이더 트랩(Spider trap)
- 어떤 정점 집합에 대하여 그 집합으로 들어오는 간선만 있고 나가는 간선이 없는 경우 발생한다.
- 이 경우 반복곱의 결과가 진동하면서 수렴하지 못하게 된다.
- 막다른 정점(Dead end)
- 어떤 한 정점에 대하여 그 정점으로 들어오는 간선만 있고 나가는 간선이 없는 경우 발생한다.
- 이 경우 반복곱의 결과가 모두 0으로 수렴한다.
위와 같은 문제를 해결하기 위해 순간이동(teleport)을 도입한다. 순간이동은 말그대로 간선의 위치와 관계없이 임의의 정점으로 순간이동하는 것을 말한다.
이에 따라 웹서퍼의 행동방식은 아래와 같이 수정된다.
1) 현재 페이지에 하이퍼링크가 없다면, 임의의 웹페이지로 순간이동한다.
2) 현재 페이지에 하이퍼링크가 있다면, 확률적으로 다음 위치를 결정한다.
2-1) $\alpha$의 확률로 하이퍼링크 중 하나를 균일한 확률로 선택해 이동한다.
2-2) $1 - \alpha$의 확률로 임의의 웹페이지로 순간이동한다.
$\alpha$를 감폭 비율(damping factor)이라고 부르며 보통 0.8정도의 값을 사용한다.
위 내용을 기반으로 알고리즘을 아래와 같이 변경할 수 있다.
1) 각 막다른 정점(dead end)에서 자신을 포함하여 모든 다른 정점으로 가는 간선을 추가한다.
- 웹서퍼 행동방식의 1번을 보정하기 위한 작업으로, 이 작업을 하면 1번을 굳이 따로 구현할 필요는 없다.
- 하지만 구현에서는 실제로 이러한 간선을 추가하지는 않는데 이는 이 포스트 후반 구현부에서 다시 알아보도록 한다.
2) 이후 모든 정점에 대하여 아래 수식을 이용한 반복곱을 수행한다.
우변의 첫번째 항은 하이퍼링크를 따라 갈 확률, 두번째 항은 순간이동을 할 확률이다. 최종적으로 이 식을 이용하면 위에서 살펴본 스파이더 트랩이나 막다른 정점의 문제가 발생하지 않는다.
페이지랭크 구현
페이지랭크 알고리즘은 NetworkX 라이브러리의 pagerank() 메소드에 구현이 되어있다.
인자로 알고리즘을 하고자하는 DiGraph 객체와 감폭 비율 alpha를 주면 알고리즘을 수행한 결과값이 (정점 식별자 : 점수) 형태의 딕셔너리 형태로 반환된다.
하지만 내부 구조를 보다 정확히 파악해보기 위해 이를 구현해보자. 여러가지 방법이 있을 수 있지만 일단 크게 3가지 방법으로 나눌 수 있을 것 같다.
1) 막다른 정점에 실제로 간선을 직접 추가한 후 iteration을 도는 방법
2) 막다른 정점에서 간선이 있다고 가정하고 계산하는 방법
3) 막다른 정점에서 사라진 페이지랭크 점수를 모든 정점에 ${1 \over \vert V \vert}$씩 나누어주는 방법
1번은 일단 비효율적이므로 생략하기로 하고, 2번과 3번에 대해 보도록 하자.
페이지랭크 구현 - 방법2
# 방법2.py
def pagerank(
graph: Graph_dict,
damping_factor: float,
maxiters: int,
tol: float,
) -> Dict[int, float]:
vec: DefaultDict[int, float] = defaultdict(float) # Pagerank vector
# Initialize the score
vertices = graph.nodes()
V = len(vertices)
for v in vertices:
vec[v] = 1 / V
# Calculate the pagerank score
for itr in range(maxiters):
vec_new: DefaultDict[int, float] = defaultdict(float)
for src in vertices:
vec_new[src] += (1 - damping_factor) / V
out_neighbors = graph.out_neighbor(src)
out_degree = graph.out_degree(src)
if out_degree == 0: # dead end(막다른 정점)
for dst in vertices:
vec_new[dst] += damping_factor * \
(vec[src] / V)
else:
for dst in out_neighbors:
vec_new[dst] += damping_factor * \
(vec[src] / out_degree)
#### Check the convergence ###
# Stop the iteration if L1norm[PR(t) - PR(t-1)] < tol
delta: float = 0.0
delta = l1_distance(vec_new, vec)
vec = vec_new
if delta < tol:
break
return dict(vec)
방법 2는 $N_{out}(i)$를 이용한 방법이다.
먼저 식을 보면 $1 - \alpha$의 확률로 src, 즉 $i$로 가게될 수 있으므로(두번째 항) 이걸 먼저 더해주고,
$\alpha$의 확률로 $i$에서 $N_{out}(i)$로 갈 수 있으므로 out-neighbors의 모든 vertices에 대하여 $i$의 점수 $r_i$(vec[src])를 균일하게 나누어준다.
out-neightbors가 없으면 막다른 정점이므로 자신의 점수를 모든 vertices에 균일하게 나누어준다.
막다른 정점이 아닌 정점일때와의 차이점은 곱해지는 값의 분모가 $\vert V \vert$인지 $d_{out}(i)$인지 뿐이다.
페이지랭크 구현 - 방법3
방법 3은 $N_{in}(i)$를 이용한다.
# 방법3.py
def pagerank(
graph: Graph_dict,
damping_factor: float,
maxiters: int,
tol: float,
) -> Dict[int, float]:
...
# Calculate the pagerank score
for itr in range(maxiters):
S = 0
vec_new: DefaultDict[int, float] = defaultdict(float)
for dst in vertices:
for src in vertices:
out_neighbors = graph.out_neighbor(src)
out_degree = graph.out_degree(src)
if dst in out_neighbors:
vec_new[dst] += damping_factor * \
(vec[src] / out_degree)
S += vec_new[dst]
leaked_pagerank = (1 - S) / V
for v in vertices:
vec_new[v] += leaked_pagerank
#### Check the convergence ###
...
코드는 $N_{out}(i)$을 이용하여 $N_{in}(i)$을 추출한 후 이를 이용했는데, 처음부터 list comprehension이나 여타 방법을 이용하여 $N_{in}(i)$을 구해놓고 이를 그대로 이용해도된다.
이 방법도 계산 자체는 방법2와 비슷하지만, dst와 src의 코드 내 위치가 달라졌음을 확인할 수 있다.
이 방법의 핵심은 모든 점수를 계산한 후 막다른 정점으로 인해 소실된(leaked) 점수를 마지막에 더해준다는 것이다.
점수의 합은 초기 설정에 의해 반드시 1이 되어야한다. 따라서 막다른 정점에서 다른 정점에 더해지지 못하고 소실된 점수는 1 - (모든 정점 점수 합)으로 구할 수 있고, 이를 모든 vertices에 균일하게 나누어준다.
원래 막다른 정점에 모든 정점으로 갈 수 있는 간선이 추가되어야하는데 이 작업을 수행하지 않았기 때문에 이러한 작업이 필요하다.
전파 모형 및 전파 최대화
실제 복잡계에도 많은 전파 현상이 일어난다. SNS나 전염병 등이 그 예이다.
이러한 전파 과정을 체계적으로 알아보기 위해 수학적 모형이 필요하다.
의사결정 기반 모형
의사결정 기반 모형은 주변 사람의 의사결정을 고려하여 각자의 의사결정을 내리는 경우에 사용된다. 선형 임계치 모형(Linear threshold model)은 의사결정 기반의 전파 모형 중 가장 간단한 형태의 모형이다.
선형 임계치 모형을 이해하기 위해 아래에서 예시를 살펴보도록 하자.
세상 모든 사람들이 B라는 휴대폰을 쓰고 있었다. 어느 날 어떤 인플루언서(얼리 어답터)들이 새로 출시된 휴대폰 A를 SNS에 광고하기 시작했다. 인플루언서들과 연결된(인플루언서들을 팔로우한) 사람들은 이를 보고 A 휴대폰을 구매하기 시작한다. 이번엔 또 새로 구매한 사람들과 연결된 사람들이 그 사람들의 영향을 받아(전파받아) A 휴대폰을 구매하기 시작한다. 이와 같이 단순히 주변인의 의사결정 비율에 따라 자신의 의사결정이 결정되는 모형을 선형 임계치 모형으로 나타낼 수 있다.
실제 세계에서도 인플루언서의 광고는 그 인플루언서를 팔로우한 다른 사람들의 구매의사를 자극할 수 있으므로 이는 어느정도 실제 세상의 모습도 반영할 수 있는 모형이다.
이 모형에서는 구체적으로 주변에 A를 사용하는 사람의 비율 ${a \over a + b}$가 일정 임계치 $q$를 넘으면 이 사람도 A를 사용하기 시작한다고 가정한다. 이 임계치는 우리가 직접 정해야하는 hyperparameter에 속한다.
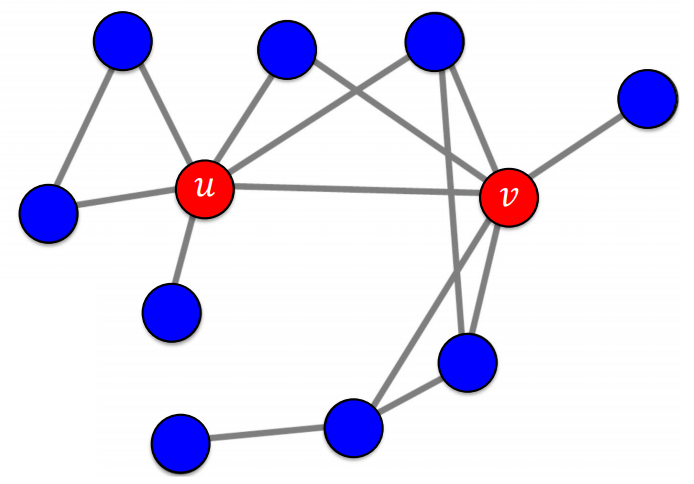
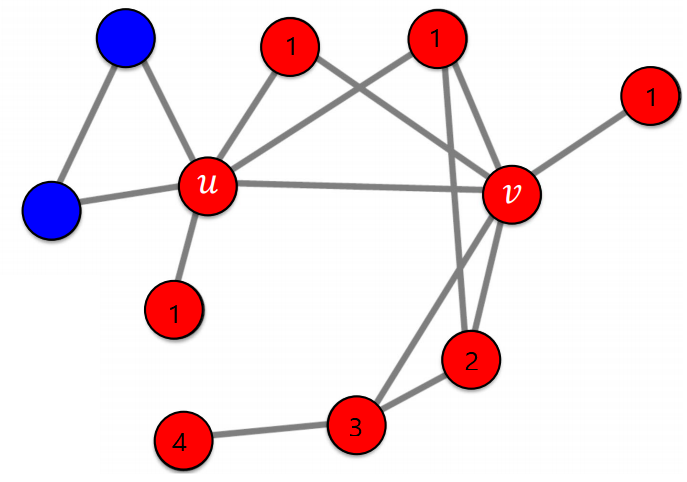
왼쪽 사진과 같이 얼리 어답터 $u$, $v$에 의해 A가 전파되기 시작했다고 하자.
얼리 어답터의 집합 {$u$, $v$}를 시드 집합(Seed set)이라고 부른다.
임계치를 55%로 잡으면, 첫 step에는(1으로 표기된 정점) 왼쪽부터 차례대로 주변인의 $1$, $1$, ${2 \over 3}$, $1$이 A를 사용하고 있으므로 임계치 55%를 넘어 이들도 A를 사용하게 된다. 두번째, 세번째, 네번쨰 step에도 역시 차례대로 주변인이 ${2 \over 3}$, ${2 \over 3}$, $1$의 비율로 A를 사용하고 있으므로 이들도 차례로 A를 선택하게 되고 더이상 바뀔 사람이 없으므로 알고리즘이 종료된다. 왼쪽 두 사람은 그 비율이 ${1 \over 2}$, 즉 50%로 임계치를 넘지 못해 그대로 B를 고수하게 된다.
확률적 전파 모형
선형 임계치 모형은 주변 사람들 중 해당 상태를 가진 사람의 비율을 보고 정점의 상태가 변화한다. 확률적 전파 모형은 비율과 관계 없이 주변 사람 중 그 상태를 가진 사람이 있으면 확률적으로 정점의 상태가 변화한다.
예를 들어 전염병의 경우, 선형 임계치 모형에서처럼 주변 사람이 많이 걸렸다고 본인도 무조건 걸리지는 않는다. 다만 주변 사람이 많이 걸렸으면 본인도 전염병에 걸릴 확률이 올라갈 뿐이다. 이렇게 확률적 과정으로 인해 전파가 되는 모형을 확률적 전파 모형이라고 하며, 여기서는 가장 간단한 형태인 독립 전파 모형(Independent cascade model)을 다루어보기로 한다.
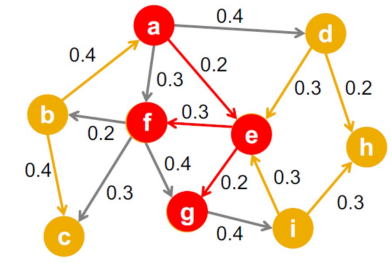
독립 전파 모형은 매우 간단하다. 간선 $(u, v)$의 가중치 $p_{uv}$는 $u$가 감염되었을 때 (그리고 $v$가 감염되지 않았을 때) $u$가 $v$에게 병을 전염할 확률이다.
이에 따라 어떤 정점 $u$가 감염되면 그 주변의 활성화되지 않은 간선들은 확률적으로 감염되지 않은 정점에게 병을 전염한다.
그리고 이 일련의 전염과정에서 각 정점이 전염될 확률은 모두 독립적이다. 그래서 이름이 독립적 전파 모형이다.
여기서도 역시 시드 집합으로부터 전염이 시작되며 이를 어떻게 정하느냐에따라 어디까지 병이 전염될지 예측해볼 수 있다. 그런데 이 모형에서 감염자는 계속 감염 상태로 남아있는 것을 가정한다. 감염자의 회복을 가정하는 전파 모형으로 SIS, SIR 등이 있다.
전파 최대화 문제
바이럴 마케팅에서 고려해야할 가장 중요한 요소 중 하나는 어떤 인플루언서를 고르냐이다. 앞서 본 전파 모형에서도 시드 집합을 어떻게 고르느냐가 전파 크기에 큰 영향을 준다. 이렇게 전파를 최대화할 수 있는 시드 집합을 찾는 문제를 전파 최대화 문제(Influence maximization)라고 부른다.
가능한 모든 경우의 수를 따질 수 있으면 좋겠지만 실제 세계는 너무나 방대하고, 정점의 개수가 조금만 커져도 그 경우의 수가 기하급수적으로 늘어난다. 따라서 우리는 보다 휴리스틱한 방법을 사용해야한다.
휴리스틱한 방법이란, 실험적/경험적으로는 잘 동작하나 그 원리를 이론적으로는 엄밀히 증명할 수 없는 문제를 말한다.
정점의 중심성(Node Centrality)
시드 집합의 크기를 $k$로 고정했을 때 정점의 중심성이 높은 순으로 $k$개의 정점을 선택하는 방법이다.
중심성을 측정하는 방법에도 여러가지가 있다.
- 페이지랭크 점수: 페이지랭크 점수가 높은 정점이 높은 중심성을 가진다.
- 연결 중심성: 연결성(degree)이 높은 정점들이 높은 중심성을 가진다.
- 근접 중심성: 각 정점에서 다른 정점들로의 평균 거리를 모두 측정한 뒤, 그 평균거리가 작은 정점들이 높은 중심성을 가진다.
- 매개 중심성: 각 정점간 최단 경로를 고려하고, 그 최단 경로에 많이 놓이는 정점일수록 정점 쌍을 연결하는 역할을 하기 때문에 높은 중심성을 가진다.
합리적인 방법이지만, 앞에서 말했듯이 최고의 시드 집합을 찾는다는 보장은 없다. 다만 실험적으로는 성능이 어느정도 보장된 방법 중 하나이다.
탐욕 알고리즘(Greedy algorithm)
탐욕 알고리즘은 시드 집합의 원소, 즉 최초 전파자를 한번에 한 명씩 선택한다.
먼저 처음에는 정점의 집합에서 첫번째 시드를 찾기 위해 $\vert V \vert$개의 정점들을 하나씩 선택해가면서 전파의 크기가 가장 큰 정점 $x$를 고른다. 다음으로는, 두번째 시드를 찾기 위해 **$x$를 포함하는 크기 2인 $\vert V \vert -1$개 집합을 하나씩 선택해가면서 전파의 크기가 가장 큰 시드 집합 {$x$, $y$}를 고른다. 이와 같은 과정을 원하는 크기가 될 때까지 반복하여 시드 집합을 찾는다.
이 방법 역시 성능이 완벽히 보장되지는 않지만 최저 성능은 수학적으로 보장되어있다.

위와 같이 전파 크기가 최대인 시드 집합에 비해 약 60% 정도의 최저성능은 보장되어있음이 수학적으로 증명되었다.
전파 모형 구현
독립적 전파 모형은 아래와 같이 구현할 수 있다.
# independent_cascade_model.py
... # 그래프 G 생성
affected = set()
affected_new = set({0}) # 시드 집합 지정
# 새로 갱신되어야 할 node는 반드시 affected_new에 들어있다.
while len(affected_new) != 0:
temp = set()
for src in affected_new:
neighbors = G.neighbors(src)
for dst in neighbors:
if (dst not in affected) and (dst not in affected_new):
p = random.uniform(0, 1)
if p < G.edges[src, dst]["weight"]:
temp.add(dst)
affected = affected | affected_new
affected_new = temp
선형 임계치 모형은 아래와 같이 구현할 수 있다.
# independent_cascade_model.py
... # 그래프 G 생성
team_A = set({4, 5}) # 시드 집합 지정
team_B = set([v for v in G.nodes if v not in team_A])
threshold = 0.7 # 임계치 지정
while True:
new_A = set()
for v in team_B:
neighbors = list(G.neighbors(v))
neighbors_A = [v2 for v2 in neighbors if v2 in team_A]
if len(neighbors_A) / len(neighbors) > threshold:
new_A.add(v)
if len(new_A) == 0:
break
team_A = team_A | new_A
team_B = team_B - new_A
draw(G, team_A)
두 모델 모두 쉽게 구현할 수 있어 별도의 설명은 생략하도록 한다.
Reference
-