Day21. 그래프 이론, 패턴 - MoonJaeHoon's blog

개요

오늘부터는 추천시스템에서 많이 활용되는 그래프 이론에 대해서 다루어보도록 한다.

아래와 같은 순서로 작성하였다.

그래프 기초
그래프 패턴
그래프 구현을 위한 파이썬 라이브러리
Reference

그래프 기초

아래는 서로 대응되는 관계이다.

그래프(Graph) - 네트워크(Network)
정점(Vertex) - 노드(Node)
엣지(Edge) - 링크(Link)

세상의 많은 것들이 복잡계(Complex System)로 이루어져있는데 이를 그래프로 표현할 수 있다.

그래프는 보통 정점의 집합 $V$와 간선의 집합 $E$로 이루어져있으며 이를 $G = (V, E)$로 표기한다.
정점의 이웃은 $N(v)$ 혹은 $N_v$로 적는다.
정점 $v$에서 나가는 이웃(Out-Neighbor)을 $N_{out} (v)$로 적는다.
정점 $v$로 들어오는 이웃(In-Neighbor)을 $N_{in} (v)$로 적는다

그래프 관련 인공지능 문제

정점 분류(Node Classification)
- 그래프의 연결관계를 통해 연결관계와 밀접하게 연관된 노드의 특성을 알 수 있고, 이 때 새로운 노드가 들어오면 해당 노드의 연결관계만으로 그 특성을 유추할 수 있다.
연결 예측(Link Prediction)
- 거시적 관점의 연결 예측. i.e. 페이스북 소셜네트워크의 크기가 얼마나 더 크게 진화할지 유추할 수 있다.
- 미시적 관점의 연결 예측. i.e. 사람과 상품 간 구매 그래프를 통해 어떤 사람이 어떤 물건을 구매할지 유추할 수 있다.
군집 분석(Community Detection)
- 연결 관계로부터 사회적 무리(social circle)을 찾아낼 수 있다.
랭킹(Ranking), 정보 검색(Information Retrieval)
- 거대한 그래프인 웹(Web)에서 어떻게 중요한 웹페이지를 찾아낼 수 있을까?
정보 전파(Information Casting), 바이럴 마케팅(Viral Marketing)
- 정보는 네트워크를 통해 어떻게 전달될 것이며, 정보의 전달을 어떻게 최대화할 수 있을까?

그래프의 유형

Undirected Graph - Directed Graph
Unweighted Graph - Weighted Graph
Unpartite Graph - Bipartite Graph

그래프의 표현

간선 리스트(Edge list): 그래프를 간선들의 리스트로 저장
- i.e. [(1, 2), (1, 5), (2, 3)]
- 방향성이 있는 경우 (출발점, 도착점) 순서로 저장
인접 리스트(Adjacent list): 각 정점의 이웃들을 리스트로 저장
- i.e. {1: [2, 5], 2: [1, 3, 5]}
- 방향성이 있는 경우 out-neighbor(혹은 in-neighbor)만 저장하거나 둘 모두를 저장할 수 있다.
- 간선 리스트로 표현할 때보다 탐색에 있어 시간복잡도가 좋다.
인접 행렬(Adjacent Matrix): 정점 수 x 정점 수 크기의 행렬로 저장
- i.e. [[0, 1, 1], [0, 1, 0], [1, 0, 0]]
- 탐색 시 시간복잡도는 좋지만 공간 복잡도면에서 비효율적이다.
- 희소 행렬(sparse matrix)로 이를 나타내면 정점의 수에 비해 간선의 수가 매우 적을 때 공간복잡도 면에서 효율이 좋다.
  
  희소 행렬은 행렬 전체를 저장하지 않고 행렬에서 1인 부분의 인덱스를 따로 저장하는 방식을 말한다.
- 다만 표현하고자 하는 그래프가 밀집(dense) 그래프인 경우 일반 행렬로 나타내는 방식이 공간 복잡도 면에서도 유리하다.

그래프 패턴

그래프의 형태와 이를 구분할 수 있는 요소들에 대해 알아보도록 한다.

실제 그래프, 랜덤 그래프

실제 그래프: 실제 복잡계로부터 얻어진 그래프
랜덤 그래프: 확률적 과정을 통해 생성한 그래프
- 에르되스-레니 랜덤 그래프(Erdős-Rényi Random Graph)
  - 에르되스-레니 랜덤 그래프 $G(n, p)$는 $n$개의 정점을 가지며, 임의의 두 정점 사이에 간선이 존재할 확률은 $p$이며 정점 간의 연결은 서로 독립적이다.

작은 세상 효과

정점 $u$, $v$ 간 경로(Path)
- $u$에서 시작하여 $v$까지 가는 연결된 정점들의 순열을 말한다.
- 경로의 길이는 해당 경로에 놓이는 간선의 수이다.
정점 $u$, $v$ 간 거리(Distance)
- $u$와 $v$ 사이의 최단 경로의 길이
그래프의 지름(Diameter)
- 정점 간 거리의 최댓값
작은 세상 효과(Small-world Effect)
- 여섯 단계 분리(Six Degrees of Separation) 실험을 통해 얻은 결과
- 실제 그래프에서 임의의 두 정점 간 거리는 생각보다 크지 않다.
- 높은 확률로 랜덤 그래프에서도 작은 세상 효과가 나타난다.
- 모든 그래프에서 작은 세상 효과가 나타나는 것은 아니다. i.e. 체인, 사이클 그래프, 격자 그래프 등

연결성의 두터운 꼬리분포

정점의 연결성(Degree)는 그 정점과 연결된 간선의 수를 의미한다. 즉, $\vert N(v) \vert$이며, $d(v)$, $d_v$로도 나타낸다.

나가는 연결성(Out Degree)
- $\vert N_{out}(v) \vert$를 의미하며 $d_{out}(v)$로도 나타낸다.
들어오는 연결성(In Degree)
- $\vert N_{in}(v) \vert$를 의미하며 $d_{in}(v)$로도 나타낸다.

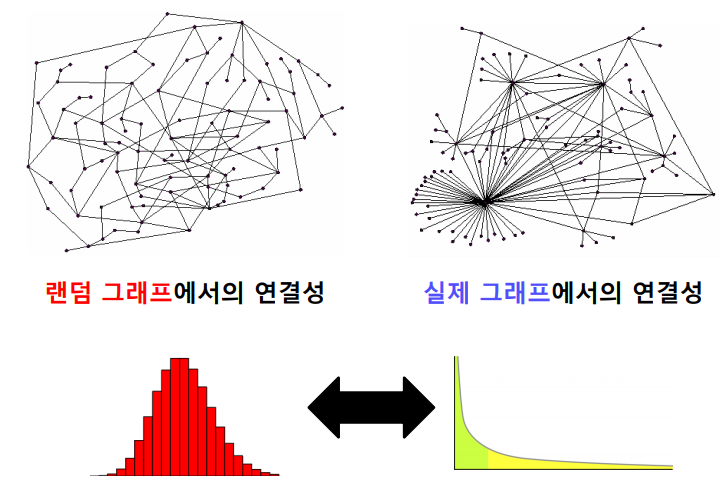
실제 그래프의 연결성 분포는 두터운 꼬리(Heavy tail)을 갖는다.
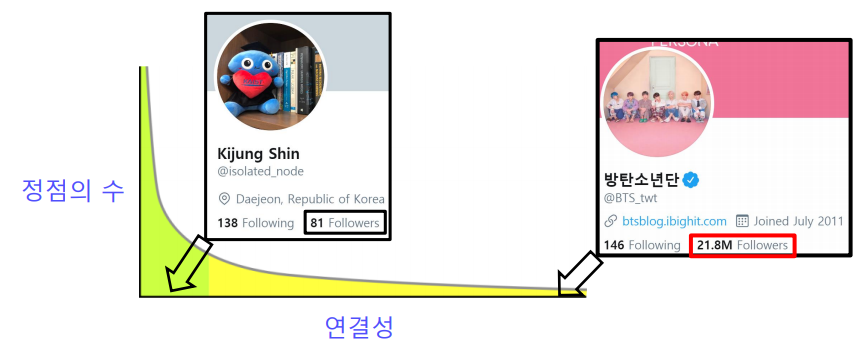
heavy_tail
위와 같이 연결성이 매우 높은 허브(Hub) 정점이 존재함을 의미한다.

대부분의 정점들은 degree가 작지만 극소수의 정점들의 degree가 매우 커 위 그림과 같이 꼬리를 형성한다.

하지만 랜덤 그래프의 연결성 분포는 높은 확률로 정규 분포와 유사하다. 확률적으로 생성되기 때문에 연결성이 매우 높은 허브가 존재할 가능성은 0에 가깝다.
heavy_tail2

군집 구조

군집(Community)이란 어떤 집합에 속하는 정점 사이에는 많은 간선이 존재하고, 그렇지 않은 정점 사이에는 적은 수의 간선이 존재하는 정점들의 집합이다. 우리가 일반적으로 생각하는 그 군집이 맞는데, 명확한 정의를 내리기에는 애매한 것 같다. 다음은 영어로 된 군집의 정의를 발췌해온 것인데, 역시나 비슷한 의미이다.

Qualitatively, a community is defined as a subset of nodes within the graph such that connections between the nodes are denser than connections with the rest of the network.

지역적 군집 계수(Local clustering coefficient)는 한 정점에서 군집의 형성 정도를 측정한다. 어떤 정점 $i$의 지역적 군집 계수는 정점 $i$의 이웃 쌍 중 간선으로 직접 연결된 것의 비율을 의미한다. 보통 이를 $C_i$로 표기한다.

한 정점을 기준으로 이웃들 간의 간선 개수가 늘어날수록 지역적 군집 계수도 증가하고, 반대로 이웃쌍 간 간선 개수가 줄어들면 지역적 군집 계수도 감소한다. 지역적 군집 계수가 매우 높다면 그 정점과 주변 정점들은 같은 군집을 형성하고 있을 가능성이 높다. 연결성이 0인 정점에서는 지역적 군집 계수가 정의되지 않는다.

전역 군집 계수(Global clustering coefficient)는 전체 그래프에서 군집의 형성 정도를 측정한다. 그래프 $G$의 전역 군집 계수는 각 정점에서의 지역적 군집 계수의 평균이다. 이 때 앞서 말한 지역적 군집 계수가 정의되지 않는 정점은 여기서 제외된다.

실제 그래프의 군집 계수는 보통 높은 편이다. 즉, 많은 군집이 존재한다. 여기에는 아래와 같은 이유가 있다.

동질성(Homophily): 서로 유사한 정점끼리 간선으로 연결될 가능성이 높다.
전이성(Transitivity): 공통 이웃이 있는 경우, 공통 이웃이 매개 역할을 해줄 수 있다.

하지만 랜덤 그래프에서는 간선이 독립적으로 형성되기 때문에 여기서는 동질성/전이성이 나타나지 않아 지역적/전역 군집 계수가 높지 않다.

거대 연결 요소

연결 요소(Connected component)는 연결이 가능한 최대 크기의 정점 집합이다.

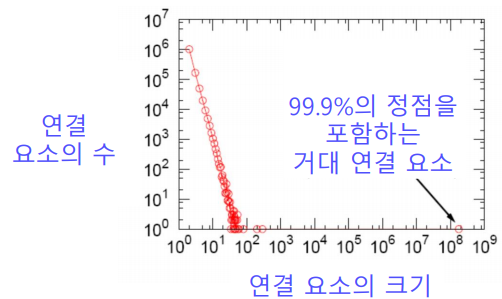
실제 그래프에서는 거대 연결 요소(Giant connected component)가 존재한다. 거대 연결 요소는 대다수의 정점을 포함한다. giant_connected_component

랜덤 그래프에도 높은 확률로 거대 연결 요소가 존재한다. 그러나 이 때 정점들의 평균 연결성이 1보다 충분히 커야한다.
giant_connected_component

랜덤 그래프의 수학적 해석

랜덤 그래프에서 각 요소는 어떤 확률 분포를 가지고 생성될까? 여기서는 우선 edge 개수의 분포 및 degree의 분포를 알아낸 후 이를 통해 local clustering coefficient의 분포를 알아낼 것이다. 그리고 이 과정에서 왜 정점들의 평균 연결성이 1보다 충분히 커야만 랜덤 그래프에 거대 연결 요소가 존재할 수 있는지에 대해 알아보도록 한다.

먼저 랜덤 그래프 $G(n, p)$에 대하여 $m$개의 edge를 가지는 임의의 network $G(n, m)$의 확률 분포를 알아보자. 이는 아래와 같이 나타낼 수 있다.

$$ P(G) = p^m (1 - p)^{ {n \choose 2} - m} $$

글씨가 작아서 헷갈릴 수 있는데, 지수에 있는 항은 $\frac{n}{2}$가 아니고 ${n \choose 2}$ 임에 주의하자.

이제 그럼 $n$과 무관하게 $m$개의 edge를 가지는 임의의 그래프 $G(m)$이 생성될 확률 분포 $P(m)$을 구해보자. 이는 간단하게 vertex쌍(총 ${n \choose 2}$개)들 중 $m$개를 고르는 확률을 구하면 알 수 있다.

$$ P(m) = { {n \choose 2} \choose m} p^m (1-p)^{ {n \choose 2} - m} $$

이제 확률변수 $m$의 확률 분포를 알았다. 그런데 마침 이 확률 분포가 $n = {n \choose m}$이고 $k = m$인 binomial distribution이다. 따라서 $m$의 기댓값은 아래와 같이 계산할 수 있다.

$$ E(m) = \bar{m} = \sum_m mP(m) = \sum_{m=0} ^{ {n \choose 2}} mP(m) = {n \choose 2} p $$

이항분포 $B(n, p)$의 기댓값은 $np$이다.

즉, 어떤 그래프의 간선의 개수는 평균 $np$개이다.

그러면 이제 degree의 기댓값을 구해보자. 이를 위해 degree $k$의 확률분포를 구해야한다. 그런데 degree는 한 vertex가 가지는 edge의 평균 개수이다. edge가 $m$개이고 vertex가 $n$개인 그래프에서 한 vertex의 degree의 기댓값은 $\frac{2m}{n}$이므로 이를 적용하면 그 값은 아래와 같다.

$$ \bar{k} = E \left(\frac{2m}{n} \right) = \frac{2}{n} \times E(m) = \frac{2}{n} \times {n \choose 2} p = (n-1)p $$

따라서 랜덤 그래프에서 한 vertex의 평균 degree $c = (n-1)p$이다.

지금까지 구한 것은 degree의 기댓값인데, 이제 degree의 확률 분포를 구해보도록 하자.

임의의 vertex가 $k$개의 vertex와 연결되어있을(즉 해당 vertex의 degree가 $k$일) 확률을 구하면 아래와 같다.

$$ p_k = { n-1 \choose k } p^k (1-p)^{n-1-k} $$

$k$개의 vertex와 연결되어있고 나머지 $n - 1 - k$개의 vertex와는 연결되지 않을 확률이다.

이 식 역시 binomial distribution으로 $G(n, p)$의 degree distribution은 binomial distribution임을 알 수 있다.

하지만 이 식을 지금부터 몇 가지의 근사식을 통해 보다 간단한 식으로 표현할 것이다. 우리는 $n$이 충분히 큰 network에 관심이 있으므로 $n$이 크다는 가정 하에(정확히는 $n$이 $k$보다 훨씬 크다는 가정 하에) 두 가지 식을 근사할 것이다.

먼저 ${ n-1 \choose k }$항을 보자. $n$이 충분히 크면 ${(n-1)! \over (n-1-k)!} \approx (n-1)^k$ 이므로

$$ {n-1 \choose k} = \frac{(n-1)!}{(n-1-k)! k!} \approx {(n-1)^k \over k!} $$

다음으로 $(1-p)^{n-1-k}$항을 보자. $p = \frac{c}{n - 1}$이므로 주어진 식에 $\log$를 취하고 근사하면 아래와 같다.

$$ \begin{aligned} \log[(1-p)^{n-1-k}] & = (n-1-k) \log ( 1- \frac {c} {n-1}) \\ &\approx -(n-1-k) { c \over n-1} \\ &\approx -c \end{aligned} $$

첫번째 근사식은 $\vert x \vert < 1$일 때 taylor expansion에 의해

$$ \ln(1 + x) = x - {x^2 \over 2} + {x^3 \over 3} - \cdots \approx x $$

임을 이용한 근사식이다. $n$이 매우 크므로 $x$의 값이 매우 작아 일차항만 남겼다. 결과적으로 $(1-p)^{n-1-k} \approx e^{-c}$임을 알았다.

이제 두 근사 결과를 종합하면 아래와 같다.

$$ p_k \approx {(n-1)^k \over k!} p^k e^{-c} ={ (n-1)^k \over k!} ({c \over n-1})^k e^{-c} = e^{-c} {c^k \over k!} $$

이 형태는 모수 $\lambda = c$인 Poisson distribution을 나타내며, $n$이 매우 큰 경우 $G(n, p)$의 degree distribution이 Poisson distribution임을 알 수 있다. 한편, 앞서 보았듯이 degree의 확률분포는 동시에 binomial distribution(Bernoulli distribution)을 만족하기도 한다.

이제 랜덤 그래프에 거대 연결 요소가 존재할 조건을 구해보자. 거대 연결 요소에 포함되는 vertex의 수를 $n_{gc}$라고 하면 임의의 vertex가 giant component에 포함될 확률은 ${n_{gc} \over n}$, 반대로 포함되지 않을 확률 $u=1-{n_{gc} \over n}$임을 쉽게 알 수 있다. 따라서 $n_{gc} = n(1-u)$이다.

이제 $u$를 이용하여 거대 연결 요소를 분석할 수 있다. 임의의 vertex $i$와 $j$가 존재한다고 하자. 그리고 $i$는 반드시 $j$를 거쳐 거대 연결 요소에 연결될 수 있다고 하자.

이 때 vertex $i$가 거대 연결 요소에 포함되지 않을 확률은 (1) $i$와 $j$가 연결되지 않을 확률과 (2) $i$와 $j$가 연결되어있으나 $j$가 거대 연결 요소에 포함되지 않을 확률의 합이다. 그 외 다른 경우는 존재하지 않는다.

먼저 (1)의 확률은 단순히 $1-p$이다. 단순히 두 vertex가 연결되지 않을 확률이기 때문이다. (2)의 확률도 간단하게 구할 수 있는데, 이는 $i$와 $j$가 연결될 확률 $p$에 $j$가 거대 연결 요소에 포함되지 않을 확률 $u$의 곱이므로 $pu$이다. 따라서 $i$가 거대 연결 요소에 포함되지 않을 확률은 이 둘의 합인 $1-p+pu$이다.

$i$가 정말 거대 연결 요소에 포함되지 않으려면 총 $n-1$개의 vertex에 대하여 모두 위 관계가 성립해야하므로 그 확률은 ${(1-p+pu)}^{n-1}$이다. 그런데 이 값은 의미상 결국 $u$와 같다. 그러므로

$$ u = {(1-p+pu)}^{n-1}, \quad p=\frac{c}{n-1} $$
$$ \begin{aligned} \log u&= (n-1) \log {\left(1-{c \over n-1} (1-u) \right)} \\ &\approx -(n-1) {c \over n-1} (1-u) \\ &= -c (1-u) \end{aligned} $$

따라서 $u=e^{-c(1-u)}$이다.

이 때 거대 연결 요소에 들어있는 vertex의 개수의 비율을 $S$라고 하면 $S = 1 - u = {n_{gc} \over n}$이므로 그 값은 아래와 같다.

$$ S = 1 - e^{-c(1-u)} = 1 - e^{-cS} $$

이 식에 따라 우리는 $S$가 $c$에 dependent하다는 것을 알 수 있다.

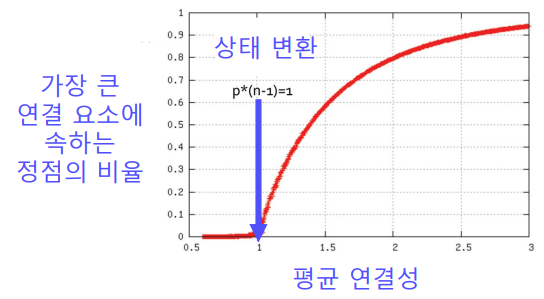
한편, 위 식에는 $S$가 좌변 및 우변에 모두 포함되어있다. 이를 풀기 위해 $y=S$ 그래프와 $y=1-e^{cS}$ 그래프의 교점을 구할 수 있고 이 그래프에서 0이 아닌 교점은 $c$가 1 이상일 때 나타나게 된다.

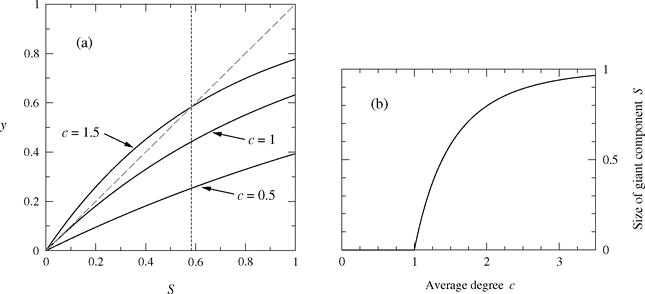
giant_connected_component_2

Reference(Network Science - Random Network (Erdös-Rényi Network))에서 발췌

좌측 그래프를 보면 $S$와 $y$에 대한 좌표축에서 $c$가 1 이상일 때부터 두 그래프간 0이 아닌 교점이 발생한다. 그리고 그 값이 커질수록 교점의 $S$ 좌표가 커진다. 이에 따라 오른쪽과 같은 그래프가 나타나게 되고, 이를 통해 degree의 기댓값이 1보다 충분히 커야만 거대 연결 요소가 존재할 수 있다는 사실을 알 수 있다.

한편, 이 그래프에 따르면, $S$는 거대 연결 요소에 포함된 vertex의 비율이므로 $c$가 클수록 거대 연결 요소의 크기가 커지게 된다는 것 역시 알 수 있다.

마지막으로 $n$이 충분히 크면 거대 연결 요소가 단 하나만 존재한다는 사실을 증명해보자. 거대 연결 요소가 2개 존재한다고 가정하면, 각각의 크기는 $S_1 n$, $S_2 n$이다. 이 두 요소가 연결되어있지 않을 확률은 각각의 연결요소에서 하나씩 뽑은 어느 두 vertex도 서로 연결되어있지 않을 확률과 같다. 이러한 distinct vertex pair $(i, j)$의 개수는 간단히 $S_1 n \times S_2 n = S_1 S_2 n^2$이므로 확률은 아래와 같다.

$$ q = (1-p)^{S_1 S_2 n^2} = \left( 1 - {c \over n-1} \right)^{S_1 S_2 n^2} $$

아까처럼 똑같이 자연로그를 취하고 $n$이 충분히 크다는 가정하에 근사식을 써보자. 이번에는 taylor expansion의 두번째 항까지 써보도록 한다. 중간중간 $n$이 크다는 가정하에 여러 근사가 이루어지므로 잘 따라가도록 하자.

$$ \begin{aligned} \log q &= S_1 S_2 \left[ n^2 \log \left( 1 - {c \over n-1} \right) \right] \\ &\approx S_1 S_2 \left[ n^2 \left( - {c \over n-1} - {1 \over 2} \left( - {c \over n-1}\right) ^2 \right) \right] \\ &= S_1 S_2 \left[ - {c n^2 \over n-1} - {1 \over 2} {c^2 n^2 \over (n-1)^2} \right] \\ &\approx S_1 S_2 \left[ -c(n+1) - {1 \over 2} c^2 \right] \\ &= c S_1 S_2 \left[-n - \left( {1 \over 2} c -1 \right) \right] \end{aligned} $$

그런데 ${n \to \infty}$이면 $\log$ 그래프의 특성에 따라 $q$가 0에 가까워진다. 즉 $n$이 충분히 클 때 서로 다른 두 거대 연결 요소는 거의 무조건 연결되어있으며, 다른 말로 거대 연결 요소가 단 하나만 존재함을 알 수 있다.

지금까지 랜덤 그래프 내에서 찾아볼 수 있는 여러 요소들에 대하여 수학적으로 접근해보았다. 추가적으로, 지금까지 본 에르되스-레니 랜덤 그래프는 현실 세계와 다소 동떨어진 면이 있다. 여기서는 추가적으로 다루지 않았지만 실제 네트워크에서 관측되는 degree distribution은 푸아송 분포의 형태가 아닌 $P(k) \approx k^{-\gamma}$의 형태를 띤다고 한다.

랜덤 그래프는 수학적으로 잘 증명되었고 이해하기 쉬운 network 모델이지만 real network와는 동떨어진 면이 존재하기 때문에 새로운 network model의 필요성이 대두된다.

그래프 별 군집 계수 및 지름 분석

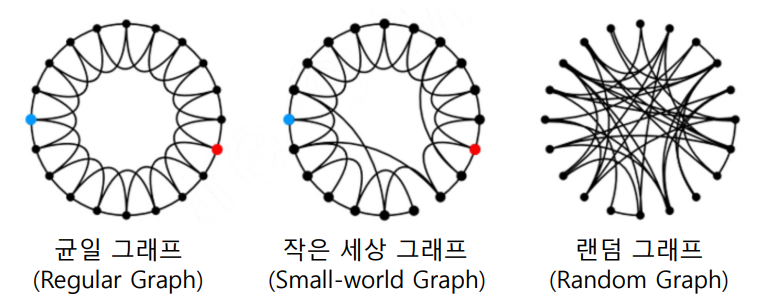
giant_connected_component

작은 세상 그래프는 균일 그래프에서 일부 간선을 랜덤한 간선으로 대체함으로써 얻을 수 있다.

균일 그래프나 작은 세상 그래프는 대부분의 정점들이 서로 연결되어있을 가능성이 높으므로 군집 계수가 크다. 반면 랜덤 그래프의 경우 앞에서 말했듯이 간선이 독립적으로 생성되므로 군집 계수가 낮다.

한편 지름의 측면에서, 균일 그래프는 멀리 있는 정점끼리 연결되는 간선이 없으므로 지름이 작다. 작은 세상 그래프나 랜덤 그래프는 멀리 있는 정점끼리 연결되는 간선이 높은 확률로 존재하므로 지름이 작다.

재차 말하지만 작은 세상 그래프가 실제 세상과 가장 유사한 형태를 띄므로, 실제 그래프 역시 일반적으로 군집 계수가 크고 지름이 작다고 볼 수 있다.

그래프 구현을 위한 파이썬 라이브러리

NetworkX는 속도는 느리지만 사용이 간편하다.
Snap.py는 속도는 빠르지만 사용이 비교적 불편하다.

둘 모두를 잘 알아두는 것이 좋으며, 여기서는 NetworkX에 대해서만 다루어보도록 한다.

# graph.py
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt

G = nx.Graph()           # 방향성이 없는 그래프
DiGraph = nx.DiGraph()   # 방향성이 있는 그래프

G.add_node(1)                    # 정점 추가
G.add_node(2)
print(str(G.number_of_nodes())   # 정점의 수 반환
# 2
print(str(G.nodes))              # 정점의 목록 반환
# [1, 2]

G.add_edge(1, 2)                 # 간선 추가

# 그래프를 시각화
# 정점의 위치 결정. spring_layout 메소드가 자동으로 결정
pos = nx.spring_layout(G) 

# 정점의 색과 크기를 지정하여 출력
nx.draw_networkx_nodes(G, pos, node_color="red", node_size=100)    

# 간선 출력
nx.draw_networkx_edges(G, pos)                                          

# 각 정점의 라벨 출력 
nx.draw_networkx_labels(G, pos, font_size=10, font_color="black")       
plt.show()

# 그래프 저장(표현)
EdgeListGraph = nx.to_edgelist(G)                  # 간선 리스트
ListGraph = nx.to_dict_of_lists(G)                 # 인접 리스트
NumpyArrayGraph = nx.to_numpy_array(G)             # 인접 행렬(일반 행렬)
SparseMatrixGraph = nx.to_scipy_sparse_matrix(G)   # 인접 행렬(희소 행렬)

# 지름/군집계수 구하기
diameter = nx.diameter(G)
average_clustering = nx.average_clustering(G)

Reference

Defining and identifying communities in networks
푸아송 분포, 직관적으로 이해하기
Network Science - Random Network (Erdös-Rényi Network)

← Previous Post Next Post →