Day16. Word Embedding

개요

오늘은 자연어 처리(NLP)의 세부 분야와 전처리 과정에 대해 간단히 알아보았다.

아래와 같이 전처리 내용 위주로 다루었다.

• NLP Intro
  • Academic Disciplines
  • Trends
• Bag-of-Words(BOW)
  • Bag-of-Words 기법의 활용
  • NaiveBayes Classifier for Document Classification
  • NaiveBayes Classifier
  • 실제 적용 예시
  • 실제 구현에서의 주의점
• Word2Vec
  • 분산 표현
  • Word2Vec 수행
  • Property and Application
• GloVe
  • Co-occurrence Matrix/Co-occurrence Probability
  • GloVe의 목적함수
  • 실제 구현에서의 주의점
• Reference

NLP Intro

NLP(Natural language processing, 자연어 처리) 분야는 신경망 구조의 머신러닝 형태가 널리 알려진 이후 가장 주목받은 분야 중 하나이다. 이 분야가 하고자하는 것은 NLU(understanding), NLG(generating) 즉 이해와 생성의 단계로 나눌 수 있다.

Academic Disciplines

자연어 처리의 학문적 분야는 여러 갈래로 나뉜다. 여기서는 주요한 세가지에 대해 알아보도록 한다.

• Natural language processing
  • 우리가 알고 있는 자연어 처리 분야이다.
  • low-level parsing(Tokenization, stemming 등) 이후 word/phrase level 단계(NER, POS tagging등)의 전처리를 거쳐 문장 단위/문단 단위/문서 단위의 처리를 거친다.
  • 감정 분석(Sentiment analysis), 번역(machine translation), 함의논리 예측(Entailment prediction), 독해 기반 질의응답(question answering), 챗봇(dialog systems), 요약(summarization)등을 수행한다.
  • 주요 학회로는 ACL, EMNLP, NAACL 등이 있다.
• Text mining
  • 텍스트 마이닝, 즉 넓게 보면 키워드 분석을 하는 분야이다.
  • 키워드를 분석하여 얻어낸 주요 단어/빈도 등을 통해 사회과학적 현상을 발견할 수 있다.
  • 마찬가지로 분석한 키워드를 통해 토픽 모델링/군집화를 수행할 수 있다.
  • 주요 학회로는 KDD, The WebConf (formerly, WWW), WSDM, CIKM, ICWSM 등이 있다.
• Information retrieval
  • 정보 검색 분야이다.
  • 지금은 크게 연구되고 있지 않은 분야이나, 이 분야는 최근 활발히 연구되는 추천 시스템과 밀접한 연관이 있다.
  • 주요 학회로는 SIGIR, WSDM, CIKM, RecSys 등이 있다.

Trends

자연어 처리 분야는 과거 딥러닝 모델이 없던 시절에는 언어학적 규칙을 기반으로 연구되었고 이후 RNN 기반 모델, 현재에 이르러서는 Transformer(self-attention)라는 모델이 이 분야를 주도하고 있다.

• rule 기반 번역은 다양한 언어의 복잡한 rule을 모두 적용하기 매우 까다로웠기 때문에 성능이 그리 좋지 않았다.
• 딥러닝 기반 모델은 기본적으로 언어학적 rule을 strict하게 적용하지 않으며 sequence data 처리에 중심을 둔다.
  • 딥러닝 모델은 text data를 벡터들의 sequence로 바라보며, 이를 위해 사전에 각 단어들을 word embedding을 통해 벡터로 변환하는 작업이 필요하다.
• transformer 이전에는 각종 NLP task들이 서로 각기 발전하였으나, transformer 이후에는 거의 모든 NLP task가 self-attention을 계속 쌓아나가는 형식으로 발전하였다.
  • 자가지도 학습(self-supervised training)을 하기 때문에 특정 task를 위한 label이 필요하지 않다. (ex. 단어를 가려놓고 머신이 해당 단어를 맞히도록 학습)
  • 따라서 구조의 큰 변화 없이 원하는 task에 적용할 수 있다.
  • BERT, GPT-3 등이 이를 적용한 모델이다. (범용적 task에 적용 가능)
• 그러나 자가지도 학습을 위해서는 대용량의 데이터와 GPU resource를 필요로 한다.

Bag-of-Words(BOW)

딥러닝 이전(신경망 없는 머신러닝 등)에 많이 활용된 벡터화 기법이다.
문장(문서)에 나타난 모든 unique한 단어들을 one-hot encoding된 벡터로 나타낸 후 문장별(문서별) 단어의 빈도수를 체크하는 방법에서 출발한다.

Bag-of-Words 기법의 활용

수업 내용에는 나오지 않았지만 BOW는 다음과 같은 두가지 대표적인 방식이 있다. TF-IDF가 더 성능이 좋을 것으로 기대되지만, 항상 그런 것은 아니다.

• 단순히 문장별로 단어 빈도를 카운팅하여 나타내는 방법(DTM)
• 전체 문서에 나타난 단어 빈도를 기반으로 카운팅하는 방법에 가중치까지 부여한 방법(TF-IDF)

NaiveBayes Classifier for Document Classification

BOW로 인코딩된 피처 벡터들을 기반으로 나이브베이즈 분류기를 사용해볼 수 있으며, 이것이 과거에 쓰이던 NLP 기법 중 하나이다. 이에 앞서, 나이브베이즈 분류기에 대해 알아보도록 하자.

NaiveBayes Classifier

이름에서 보이듯이 베이즈 이론을 적용한 모델이다. 과거의 데이터를 기반으로 확률 분포를 파악하여 이를 기반으로 타겟값을 예측하는 방법이다. 우리가 현재 하고자하는 바에 맞춰, $d$를 문서의 수, $c$를 클래스의 수(i.e. 문서의 topic class)라고 하자. $C$는 분류하고자 하는 클래스 전체 집합이고, $w$는 어떤 문서의 단어 sequence이다.

$$ \begin{aligned} C_{\text{MAP}} &= \underset{c \in C}{\mathrm{argmax}} P(c \vert d) \\ &= \underset{c \in C}{\mathrm{argmax}} \dfrac{P(d \vert c) P(c)}{P(d)} \\ &= \underset{c \in C}{\mathrm{argmax}} P(d \vert c) P(c) \end{aligned} $$

여기서 ‘MAP’은 maximum a posterior의 약자로, 사후확률이 최대인 것 즉 가장 정답에 가까운 class를 찾는다는 뜻이다. 이것이 Naive bayes classifier의 핵심 decision rule이다. 첫번째 줄에 Bayes Rule이 적용되어 두번째 줄이 도출되었고, evidence(분모)는 여기서 고정값(상수값)이므로 세번째 줄에서는 제거된다. $P(d)$는 어떤 문서 $d$가 뽑힐 확률이기 때문에 상수값이라고 볼 수 있기 때문이다. 따라서 argmax를 행하는데에 있어 분모의 값은 크게 중요하지 않게 된다.

또 중요한 것이 있는데, 나이브 베이즈 분류기는 주어진 class의 각 특징(즉, 단어)들이 서로 조건부 독립이라는 가정을 한 상태로 돌아간다. 실제로 클래스 내 특징(단어)들간의 상관관계가 있을 수 있지만 일단은 이를 고려하지 않는다. 복습을 하자면, 조건부 독립에서는 아래와 같은 식이 성립한다.

$$ \text{If} \;\; x \perp y \vert z, \;\;\text{then} \;\;\; p(x \vert y, z) = p(x \vert z) $$ $$ \begin{aligned} P(x_1, x_2 \vert y) &= P(x_1 \vert x_2, y) P(x_2 \vert y) \\ &= P(x_1 \vert y) P(x_2 \vert y) \end{aligned} $$

따라서 각 class에 대하여 $n$개의 word들이 조건부 독립이라고 가정하면

$$ P(d \vert c) P(c) = P(w_1, w_2, \cdots, w_n \vert c)P(c) \rightarrow P(c) \prod\nolimits _{w_i \in W} P(w _i \vert c) $$

따라서 우리가 구하고자 하는 바는

$$ \underset{c \in C}{\mathrm{argmax}} P(c) \prod\nolimits _{w_i \in W} P(w _i \vert c) $$

이 된다.

실제 적용 예시

아래와 같이 train data가 주어졌다고 하자.

Doc(d)	Document (words, w)	Class(c)
1	Image recognition uses convolutional neural networks	CV
2	Transformer can be used for image classification task	CV
3	Language modeling uses transformer	NLP
4	Document classification task is language task	NLP

test data(document)로 “Classification task uses transformer”이 주어졌을 때 어떻게 분류를 할 수 있을까?

우선 CV가 4개 중 2개, NLP도 4개 중 2개이므로 각 클래스에 대한 확률 $P(c_{\text{cv}}) = \dfrac{1}{2}$, $P(c_{\text{NLP}}) = \dfrac{1}{2}$는 쉽게 알 수 있다.

test data에 나타난 각 단어 $w_i$에 대하여 각 클래스 $c_i$에 대한 확률 분포를 구해보자. 단어 $w_k$가 주제가 $c_i$인 문서에 나온 횟수가 $n_k$일 때, $P(w_k \vert c_i) = \dfrac{n_k}{n}$이다.

Word	Prob	Word	Prob
$P(w_{\text{“classification”}} \vert c_\text{CV})$	$\dfrac{1}{14}$	$P(w_{\text{“classification”}} \vert c_\text{NLP})$	$\dfrac{1}{10}$
$P(w_{\text{“task”}} \vert c_\text{CV})$	$\dfrac{1}{14}$	$P(w_{\text{“task”}} \vert c_\text{NLP})$	$\dfrac{2}{10}$
$P(w_{\text{“uses”}} \vert c_\text{CV})$	$\dfrac{1}{14}$	$P(w_{\text{“uses”}} \vert c_\text{NLP})$	$\dfrac{1}{10}$
$P(w_{\text{“transformer”}} \vert c_\text{CV})$	$\dfrac{1}{14}$	$P(w_{\text{“transformer”}} \vert c_\text{NLP})$	$\dfrac{1}{10}$

예를 들어, $P(w_{\text{“task”}} \vert c_\text{CV})$는 CV 문장에 단어가 총 14개, 그 중 task가 1번 등장했으므로 $\dfrac{1}{14}$임을 알 수 있다.

따라서 $d = \text{“Classification task uses transformer”}$에 대하여,

$$ P(c_\text{CV} \vert d) = P(c _\text{CV}) \prod _{w \in W} P(w \vert c _\text{CV}) = \dfrac{1}{2} \times \dfrac{1}{14} \times \dfrac{1}{14} \times \dfrac{1}{14} \times \dfrac{1}{14} \approx 0.000013 $$ $$ P(c_\text{NLP} \vert d) = P(c _\text{NLP}) \prod _{w \in W} P(w \vert c _\text{NLP}) = \dfrac{1}{2} \times \dfrac{1}{10} \times \dfrac{2}{10} \times \dfrac{1}{10} \times \dfrac{1}{10} \approx 0.0001 $$

이에 따라 문장 $d$는 확률이 더 높은 NLP로 분류된다.

실제 구현에서의 주의점

• laplace smoothing
  어떤 클래스에 input에 나온 단어가 한 개도 존재하지 않으면 다른 단어가 아무리 많이 나와도 조건부 확률이 0이 나오게되는 상황이 발생한다. 이를 방지하기 위해 나이브베이즈 분류에서는 laplace smoothing 등의 regularization 기법 등을 추가로 이용하게 된다.

  laplace smoothing을 해주면 한 word에 대한 likelihood에서 smoothing 상수가 분모, 분자에 더해지게 되어 아래와 같게 된다.

  $$ P(w_k \vert c_i) = \dfrac{n_k + \alpha}{n + \alpha * K} $$

  여기서 $\alpha$는 hyper parameter(smoothing parameter)이다. $K$는 데이터의 개수(즉 원핫 벡터의 차원)이다. 일반적으로 $\alpha$ 값으로 1을 많이 사용한다.

• likelihood with log
  조건부확률 값 계산시 $\prod\nolimits _{w_i \in W} P(w _i \vert c)$ 라는 식을 사용하게 되는데, 단어의 수가 많아질수록 0과 1사이의 값을 여러번 곱하다보면 컴퓨터가 제대로된 계산을 하지 못하게 되는 상황이 발생하게 된다.

  따라서 실제 구현에서는 구한 각 likelihood에 log를 취하여 더해주는 방식으로 원하는 값을 구하고 예측을 수행한다.

  $$ \log \left(\prod\nolimits _{w_i \in W} P(w _i \vert c) \right) = \sum\nolimits _{w_i \in W} \log P(w _i \vert c) $$

  여기에 마지막으로 log를 취한 prior를 더해주면 원하는 조건부 확률을 최종적으로 얻을 수 있다.

Word2Vec

기존 one-hot encoding 기반 단어 벡터화는 희소 벡터가 생성되기 때문에 공간적 낭비가 커지게 되며 단어 자체의 의미를 벡터 수치 값이 지니지 못한다. 따라서 차원을 줄이고 수치 자체에 의미를 담은 밀집 벡터(dense vector)로 단어를 벡터화하면 좋은데, 이를 워드 임베딩(word embedding)이라고 한다.

분산 표현

워드 임베딩도 여러가지가 있는데, 여기서 다루고자하는 Word2Vec, GloVe는 모두 분산 표현을 목표로 하는 임베딩이다. 분산 표현이란 분포 가설(distributional hypothesis)에 기반한 표현 방법으로, 비슷한 위치에서 등장하는 단어들은 비슷한 의미를 가진다라는 가정이다. 이 가정을 통해 생성된 임베딩 벡터들은 “한국 - 서울 + 도쿄 = 일본” 와 같은 연산이 수행 가능한데, 이것은 임베딩 벡터에 단어간 유사도가 반영되었기 떄문이다.

Word2Vec 수행

Word2Vec에는 CBOW(Continuous Bag of Words)와 Skip-Gram 두 가지 방법이 있다. 두 방법 모두 중심 단어와 주변 단어(사전에 정의한 window size가 주변의 기준이 됨)가 비슷한 의미를 가진다는 것(분포 가설)을 학습시킴으로써 임베딩 벡터를 얻는 방법이다. 차이점을 보면 CBOW는 input, output으로 (주변단어, 중심단어)가 들어가고 반면 Skip-Gram은 (중심단어, 주변단어)가 들어가게 된다. 방법도 약간의 차이가 있지만 거의 유사하다고 보면 된다. 다만 많은 논문에서 성능 비교시 Skip-Gram이 대체로 더 우수한 성능을 가지고 있다고 알려져 있으며, 역시 이 수업에서는 Skip-Gram 방법만을 다루었다.

Skip-Gram 방법을 살펴보자.
먼저 문서에 나타난 모든 단어들을 one-hot encoding한 후, 앞서 말했듯이 중심단어의 원핫벡터가 입력으로 들어갔을 때 출력으로 주변단어의 원핫벡터가 출력으로 나오도록 가중치를 학습시키면 된다. 여기서 hidden layer의 차원은 hyper parameter인데, hidden layer의 차원수가 곧 임베딩 벡터의 차원수가 된다.

예를 들어 “I study math”라는 문장은 {“I”, “study” “math”}로 이루어져 있으므로 중심단어를 “study”로 보았을 때 window size를 3으로 하면 주변단어 “I”, “math”가 잘 나오도록 가중치를 학습시키면 된다.

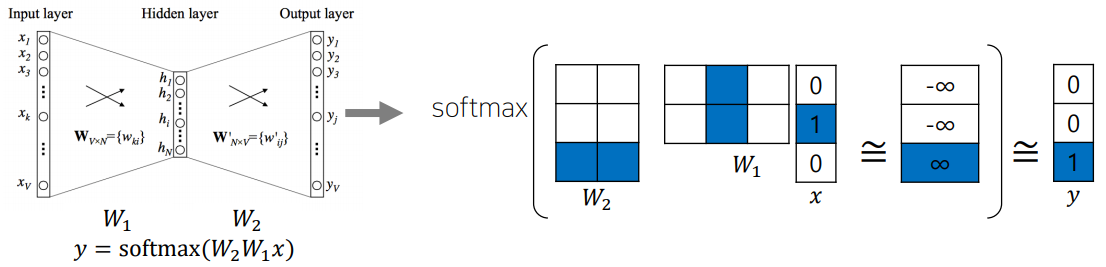
여기서는 Input: “study” [0, 1, 0], Output: “math” [0, 0, 1]을 예시로 보자. input인 study의 원핫벡터는 레이어를 통과하여 output으로 math의 원핫벡터가 나와야한다.

눈여겨 볼 점은 원핫 벡터의 특성상 결국 $W_1$의 2번째 column이 hidden layer로 들어오게 되므로 사실 이부분은 행렬곱이 아니라 해당 위치의 column vector를 뽑아온다고 생각하면 된다.
또한 역으로 생각하면 $W_2$의 3번째 row가 math의 원핫벡터에 직접적 영향을 주게 되므로 사실 위 그림에서 색칠된 이 두 벡터가 여기서 가장 중요한 벡터들이다.

output에 대하여 softmax를 취하므로 raw output은 $\left[ -\infty, -\infty, \infty \right]$가 나오도록 하는 것이 학습의 목표이며, 학습의 결과로 나온 색칠된 벡터들 즉 $W_1$의 2번째 column, $W_2$의 3번째 row는 각각 study를 나타내는 벡터, math를 나타내는 벡터가 된다.

이렇게 하여 최종 결과로 나온 $W_1 ^\text{T}$와 $W_2$ 중 어떤 것이든 임베딩 벡터로 사용해도 상관 없는데, 통상적으로 $W_1 ^\text{T}$를 임베딩 벡터로 사용하게 된다.

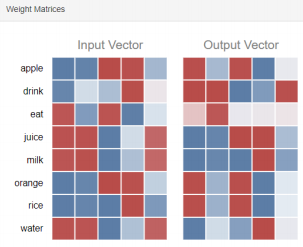
유사한 단어의 임베딩 벡터간의 내적값이 최대로 되도록 학습시켰는데, 위 그림에서 보다시피 학습 결과를 보면 비슷한 위치에 놓일 만한 단어들간의 내적 값은 매우 크다.

예를 들어 eat(input), apple(output) 쌍이나 drink(input), juice(output) 쌍 등은 유사한 벡터표현을 보이며, 따라서 이 둘 간의 내적값이 최대한 커질 수 있다. 한편, 같은 input vector 내에서 보면 drink와 관련이 있는 milk, water 역시 유사한 형태를 띄고 있다.

따라서 만약 input이 eat으로 들어오면 모델은 그 결과로 apple, orange, rice 등의 output을 내놓을 것으로 예상할 수 있다. (내적값이 크기 때문에 softmax의 결과값이 클 것이다)

Property and Application

실제로 이렇게 학습된 임베딩 벡터들은 유사 의미관계를 보이는 벡터들간의 비슷한 위치관계를 보인다.
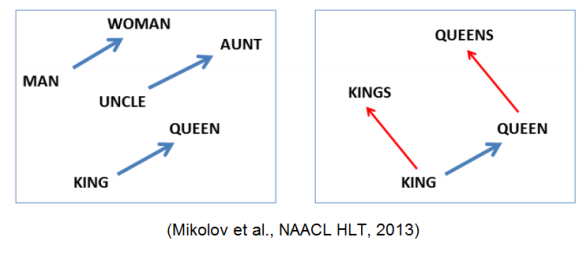
예를 들어, vec[queen] - vec[king] $\approx$ vec[woman] - vec[man] (여성-남성의 위치관계가 비슷)임을 알 수 있다.

Word2Vec으로 생성된 임베딩 벡터로는 아래와 같은 적용을 해볼 수 있다.

• Intrusion Detection(여러 단어 중 의미가 가장 상이한 것을 탐색)
  • 주어진 단어들 중 다른 단어들간의 Euclidean distance의 평균이 가장 큰 단어가 detectino에 걸린다.
  • i.e. math, shopping, reading, science가 주어졌을 때 타 단어들간의 유클리드 거리의 평균이 가장 큰 단어인 shopping이 detection에 걸린다.
• 대부분의 NLP 분야에 활용될 수 있다.
  • 번역 시 서로 다른 언어여도 같은 의미를 가진 단어들은 임베딩 벡터들이 동일하게 align될 가능성이 높으므로 번역 성능을 높일 수 있다.
  • 그 외에도 sentiment analysis, image captioning 등에 활용될 수 있다.

GloVe

GloVe(Global Vectors for Word Representation, 글로브)는 Word2Vec에 단어 빈도수에 대한 정보까지 포함하여 워드 임베딩을 수행한 방법이다.
꼭 Word2Vec보다 성능이 항상 좋은 건 아니고, 상황에 따라 더 좋은 성능을 보이는 것을 골라 쓰면 될 듯하다.

LSA(SVD를 이용한 방법)는 단어 의미 유추 작업(위에서 본 단어 짝 맞히기)에 약점을 보이며, Word2Vec은 윈도우 사이즈 밖의 단어들의 의미를 고려하지 못한다. 따라서 각각의 한계를 극복하여 LSA의 카운트 기반 방법과 Word2Vec의 예측 기반 방법을 결합하여 나오게 된 방법이 GloVe이다.

Co-occurrence Matrix/Co-occurrence Probability

• Co-occurrence Matrix(동시등장행렬)
  • 동시 등장 행렬은 윈도우 크기 N일 때 중심 단어 주변 N개 단어들의 빈도를 나타낸 행렬이다.
    1. I like deep learning
    2. I like NLP
    3. I enjoy flying

  • 위와 같이 세 문장이 주어졌을 때, window size n = 1이면 동시등장행렬은 아래와 같다.

    카운트	I	like	enjoy	deep	learning	NLP	flying
    I	0	2	1	0	0	0	0
    like	2	0	0	1	0	1	0
    enjoy	1	0	0	0	0	0	1
    deep	0	1	0	0	1	0	0
    learning	0	0	0	1	0	0	0
    NLP	0	1	0	0	0	0	0
    flying	0	0	1	0	0	0	0

  • 이는 당연히 symmetric matrix이다.
• Co-occurrence Probability(동시 등장 확률)
  • 동시 등장 확률은 $P(k \vert i)$로, 특정 단어 $i$가 등장했을 때 어떤 단어 $k$가 등장할 확률이다.
  • 단순히 $i$번째 행의 모든 값을 더하여 분모로 하고 $(i, k)$ 성분을 분자로 하면 구할 수 있다.
  • $i$가 고정된 상태에서 $k$가 어떤 값을 가지느냐에 따라 동시 등장 확률이 달라질 수 있다.
  • 동시등장확률에서 주의깊게 보아야 할 것은 두 동시등장확률 사이의 비이다.
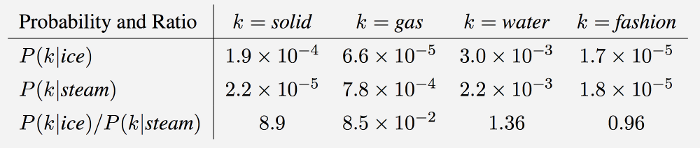
    • solid와 관련이 큰 ice, solid와 관련이 적은 steam 간의 동시등장확률비는 1과 멀다.
    • gas와 관련이 큰 solid, gas와 관련이 적은 ice 간의 동시등장확률비는 1과 멀다.
    • water은 ice 및 solid와 모두 관련이 크기 때문에 동시등장확률비가 1에 가깝다.
    • fashion은 ice 및 solid와 모두 관련이 적기 때문에 동시등장확률비가 1에 가깝다.
    • $P(k \vert i_1)$과 $P(k \vert i_2)$ 사이의 비가 1에 가까울수록 단어 $k$와 두 단어 $i_1$, $i_2$간의 관계가 유사함을 의미한다.

GloVe의 목적함수

우선 GloVe에서는 임베딩 된 중심 단어와 주변 단어 벡터의 내적이 전체 말뭉치(corpus)에서의 동시 등장 확률이 되도록 만드는 것이 목표이다. 이를 아래와 같이 표현하였다.

$$ dot\ product(w_{i}\ \tilde{w_{k}}) \approx\ P(k\ |\ i) = P_{ik} $$

이제 우리는 이를 만족하는 임베딩 벡터를 찾기 위해 단어 간의 관계를 잘 표현하는 함수를 구해야한다. 우리가 찾고자 하는 함수 $F$는 아래와 같이 나타낼 수 있다.

$$ F({ w }_{ i },{ w }_{ j },\tilde { { w }_{ k } } )=\frac { { P }_{ ik } }{ { P }_{ jk } } $$

여기서 $P_{ik} = P(k \vert i)$를 의미한다. 즉, 앞서 보았던 동시등장확률간 비를 표현한 표를 참고하면, 아래와 같은 예시를 들 수 있다.

$$ F({ w }_{ ice },{ w }_{ steam },{ w }_{ solid })=\frac { { P }_{ ice,solid } }{ { P }_{ steam,solid } } =\frac { P(solid|ice) }{ P(solid|steam) } =\frac { 1.9\times { 10 }^{ -4 } }{ 2.2\times { 10 }^{ -5 } } =8.9 $$

위 조건을 만족하는 함수 $F$를 찾는 것이 목표이다.

$dot\ product(w_{i}\ \tilde{w_{k}}) \approx\ F(W_{i} ^T W_{k}) \approx\ P(k \vert i) = P_{ik}$라 하면

$$ \begin{align*} F({ w }_{ i }-{ w }_{ j },\tilde { { w }_{ k } } )&=\frac { { P }_{ ik } }{ { P }_{ jk } } \\ F({ { ({ w }_{ i }-{ w }_{ j }) }^{ T } }\tilde { { w }_{ k } } )&=\frac { { P }_{ ik } }{ { P }_{ jk } } \\ F({ { ({ w }_{ i }-{ w }_{ j }) }^{ T } }\tilde { { w }_{ k } } )&=\frac { F({ w }_{ i }^{ T }\tilde { { w }_{ k } } ) }{ F({ w }_{ j }^{ T }\tilde { { w }_{ k } } ) } \\ F({ w }_{ i }^{ T }\tilde { { w }_{ k } } -{ w }_{ j }^{ T }\tilde { { w }_{ k } } )&=\frac { F({ w }_{ i }^{ T }\tilde { { w }_{ k } } ) }{ F({ w }_{ j }^{ T }\tilde { { w }_{ k } } ) } \end{align*} $$

와 같이 나타낼 수 있다.

다음으로, $F$는 중심단어가 바뀌어도 식이 같은 값을 반환해야한다. 예를 들어 $w_i$와 $\tilde{w_k}$의 위치가 서로 바뀌어도 식이 같은 값을 반환해야한다. 중심단어와 주변단어의 선택 기준은 무작위 선택이기 때문이다. 따라서 준동형(homomorphism)을 만족해야한다. 준동형이란 간단히 말하면 $F(a+b) = F(a)F(b),\ \forall a,\ b\in \mathbb{R}$을 만족하는 함수이다.

이를 만족하는 함수로는 지수함수를 떠올릴 수 있다. $F$를 $exp$로 치환하여 식을 나타내면 아래와 같다.

$$ exp({ w }_{ i }^{ T }\tilde { { w }_{ k } } -{ w }_{ j }^{ T }\tilde { { w }_{ k } } )=\frac { exp({ w }_{ i }^{ T }\tilde { { w }_{ k } } ) }{ exp({ w }_{ j }^{ T }\tilde { { w }_{ k } } ) } $$ $$ { w }_{ i }^{ T }\tilde { { w }_{ k } } =\log { { P }_{ ik } } =\log { X_{ ik }-\log { X_{ i } } } $$

그런데 이 상태에서는 중심단어와 주변단어 $w_i$와 $\tilde{w_k}$의 위치가 서로 바뀌었을 때 식이 성립하지 않는다. 왜냐하면 $\log(P_{ik}) = \log(P_{ki})$여야하는데, $\log(X_{ik}) = \log(X_{ki})$이지만 $\log(X_i) \neq \log(X_k)$이므로 $\log(X_{ik}) - \log(X_i) \neq \log(X_{ki}) - \log(X_k)$이기 때문이다.

따라서 $\log(X_i)$, $\log(X_k)$를 상수항($b_i$, $b_k$)로 처리하여 식을 나타내게 된다.

$$ { w }_{ i }^{ T }\tilde { { w }_{ k } } =\log { X_{ ik }-{ b }_{ i }-\tilde { { b }_{ k } } } $$ $$ { w }_{ i }^{ T }\tilde { { w }_{ k } } +{ b }_{ i }+\tilde { { b }_{ k } } =\log { X_{ ik }} $$

위와 같은 상태에서는 $i$와 $k$를 바꾸어도 값의 변화가 없다.

이제 식을 보면, $X_{ik}$는 우리가 사전에 구한 값이므로 $\log(X_{ik})$의 값을 우리는 이미 알고 있다. 따라서 이를 최소화하는 $w$들과 $b$들을 찾는 것이 우리의 목표이다.

우리는 아래와 같은 식을 최소화시키도록 $w$들과 $b$들을 학습시키면 된다.

$$ J=\sum _{ i,j=1 }^{ V }{ { ({ w }_{ i }^{ T }\tilde { { w }_{ j } } +{ b }_{ i }+\tilde { { b }_{ j } } -\log { X_{ ij } } ) }^{ 2 } } $$

그런데 $X_{ij}$ 값이 지나치게 작거나, 지나치게 클 때(즉, 함께 나타나는 빈도가 너무 적거나 너무 많을 때)는 이 값을 그대로 적용하면 학습에 도움이 되지 않는다. 따라서 이러한 위험을 제거하기 위해 아래와 같은 함수 $f$를 손실함수에 곱하게 된다.

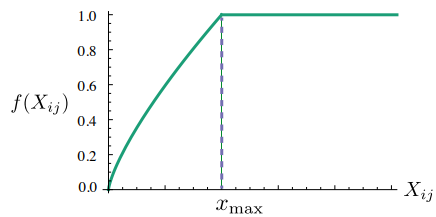
이 함수를 이용하면 빈도가 적은 단어는 0에 가까운 가중치를 얻게 되고, 지나치게 많은 단어는 가중치에 한계를 줄 수 있게 된다.

$$ J=\sum _{ i,j=1 }^{ V }{ { f\left( { X }_{ ij } \right) ({ w }_{ i }^{ T }\tilde { { w }_{ j } } +{ b }_{ i }+\tilde { { b }_{ j } } -\log { X_{ ij } } ) }^{ 2 } } $$ $$ where\quad f(x)=\begin{cases} { (\frac { x }{ { x }_{ max } } ) }^{ \alpha } \\ 1\quad otherwise \end{cases}if\quad x<{ x }_{ max } $$

일반적으로 $f$에서 $\alpha = 0.75$의 값을 많이 활용한다.

GloVe 방법은 co-occurrent matrix를 찾기 위해 matrix decomposition을 해야하므로 계산복잡성이 커지는 단점이 있다.

다만 성능이 좋은 편에 속하며, 특히 수많은 단어에 대한 임베딩 벡터가 공개되어있기 때문에 실제로 활용하기 간편하다는 장점이 있다. (물론 Word2Vec도 임베딩 벡터 셋이 공개되어있다고 한다)

실제 구현에서의 주의점

앞서 input x로 one-hot encoding된 벡터가 들어간다고 설명했지만, 실제 PyTorch 구현에서는 nn.Embedding 객체를 사용하기 때문에 정수 인덱스를 그대로 넣어주게 된다. 여기서 nn.Embedding 객체는 그저 lookup table의 역할을 한다. 쉽게 말하면, 정수 인덱스 하나를 x로 주면 그 인덱스에 맞는 벡터를 자신이 가지고 있는 가중치에서 반환(y)하는 함수 같은 역할을 하는 것이다.

따라서 초기 parameter 값을 넣어주지 않은 채로 초기화된 embedding 객체는 parameter가 전부 random 값으로 초기화되어있고((0, 1) normal distribution 기반) 이후 optim과 loss를 사용하여 embedding 객체 내의 파라미터들을 학습시키면 비로소 우리가 원하는, 관계성이 반영된 임베딩 벡터를 얻을 수 있다.

또한 Embedding 객체에서는 embedding vector를 받아오고 싶을 때 input(정수 index)으로 LongTensor type을 기대하기 때문에 Embedding 모듈 사용시에 이에 주의하도록 하자. (텐서는 그냥 생성하면 default로 FloatTensor가 생성되기 때문에 이러한 작업이 필요하다)

Reference

Naive Bayes Classification
워드투벡터(Word2Vec)
GloVe를 이해해보자!

---