Day15. Generator

개요

Generative Model에 대해 알아보고, 대표적인 generative model인 VAE, GAN에 대해 자세히 알아보았다.

오늘은 아래 내용을 다루었다.

• Generator
  • Discrete Distributions
  • 필요한 parameter의 수
  • Conditonal Independence
  • Auto regressive Model (AR model)
• Variational Auto-Encoder, VAE
  • Autoencoder
  • Variational Auto-encoder
• Generative Adversarial Network, GAN
  • Generative Adversarial Network
  • 실제 구현과 논문의 차이점
  • GAN 변형 모델
• Reference

Generator

Genarative model이란 학습 데이터의 분포를 따르는 유사한 데이터를 생성해내는 모델이다. 근데 사실 실제로는 생성뿐만 아니라 더 많은 기능을 수행할 수 있다.

여기서는 학습을 통해 학습 데이터의 분포 $p(x)$를 찾는 것이 주요 목적이다.
그리고 이 확률분포 $p(x)$를 이용해 아래와 같은 task를 수행할 수 있다.

1. Generation
   • 만약 우리가 $x_{\text{new}} \sim p(x)$ 인 $x_{\text{new}}$를 샘플링한다고하면, $x_{\text{new}}$는 우리가 원하는 것이어야 한다.
   • i.e. 만약 우리가 개에 대한 이미지를 학습했다면, $x_{\text{new}}$는 개처럼 생겨야 한다.
2. Density estimation
   • 넣어준 이미지에 대하여 이미지가 우리가 원하는 것에 가깝다면 $p(x)$가 높아야 하며, 가깝지 않다면 $p(x)$는 낮아야 한다.
   • i.e. $x$가 개와 닮았다면 $p(x)$의 값이 높고, 아니면 낮다.
   • 이를 통해 anomaly detection(이상 행동 감지)을 할 수 있다. 평소와 다른 행동에 대하여 $p(x)$의 값은 낮게 나타날 것이다.
   • 이것은 마치 discriminative model(일반적인 분류 문제)과 같은 역할을 한다.
   • 그래서 사실 generative model은 엄밀히 말하면 discriminative model을 포함하고 있다.
   • 이렇게 두 속성을 모두 가진 모델을 explicit model이라고 부르며, 단순히 generation만 수행하는 VAE, GAN 등의 모델은 implicit model이라고 나타낸다.
3. Unsupervised representation learning(feature learning)
   • 이 이미지가 보통 어떤 특성을 가지는지 스스로 학습해낸다.
   • i.e. 개에게 귀가 있고 꼬리가 있고, …

Discrete Distributions

우리는 확률분포를 explicit하게 나타낼 수 있는 explicit model(tractable density)에 대해 다뤄볼 것이다. 학습을 어떻게 시키는지를 보기 이전에, 보고 지나가야할 것들이 많다.
먼저 가장 대표적인 이산확률분포 몇 가지를 다시 짚고 넘어가자.

• Bernoulli distribution
  • 나올 수 있는 경우가 2개인 경우의 확률 분포이다
  • $X \sim \text{Ber}(p)$
  • parameter $p$하나로 모든 확률을 표현할 수 있다.
• Categorical distribution
  • 나올 수 있는 경우가 $n$개인 확률 분포이다.
  • $Y \sim \text{Cat}(p_1, \cdots, p_n)$
  • 어떤 한 상황의 확률은 전체 확률 1에서 나머지 확률을 빼줌으로써 구할 수 있으므로 parameter는 $n-1$개 필요하다.

parameter 개수 이야기를 하고 있는데, 그 이유는 주어진 학습 데이터의 확률 분포를 나타내기 위해 몇 개의 파라미터가 필요한지를 먼저 찾아야 하기 때문이다.

필요한 parameter의 수

다음 예시를 보자.

• 28 x 28 binary pixel 이미지의 확률 분포를 찾으면 이 때 parameter 수는?
  • 이 이미지는 binary pixel로 이루어져 있으므로 나타낼 수 있는 이미지의 경우의 수는 $2^{(28*28)} = 2^{768}$개이다.
  • 여기서 중요한건 이 이미지에 있는 픽셀들간 상호 독립적이라는 보장이 없다는 것이다.
  • 따라서 모든 픽셀이 서로 dependent하다고 가정하면 확률 분포 $p(x_1, \cdots, x_{2^{768}})$의 parameter 수는 $2^{768} - 1$개이다.
• 만약 위 문제에서 각 픽셀 $X_1, \cdots, X_n$이 서로 독립이면, 몇 개의 parameter가 필요할까?
  • 픽셀들이 서로 독립이므로 다음이 성립한다.
  $p(x_1, \cdots, x_{n}) = p(x_1)p(x_2)\cdots p(x_n)$
  • 따라서 이 경우 각각에 대한 확률값만 parameter로 나타내면 되므로 $n$개의 parameter가 필요하다.
  • 하지만 실제로는 이렇게 모두가 독립인 경우는 존재할 수가 없다.

극단적인 두 가지 경우를 살펴보았다. 전자는 parameter가 말도 안되게 많고, 후자는 현실 세계에 적용할 수가 없다. 따라서 우리는 이 사이 중간 어딘가를 찾아야한다.

Conditonal Independence

다음 세가지 rule을 짚고 넘어가자.

1. Chain rule $$ p(x_1, \cdots, x_n)=p(x_1)p(x_2 \vert x_1)p(x_3 \vert x_1,x_2) \cdots p(x_n \vert x_1,...,x_{n-1}) $$
   • 결합확률 분포를 위와 같이 나타낼 수 있다. 직관적으로 이해 가능하다.
   • Chain rule은 확률변수간 dependent 여부와 관계 없이 성립한다.
   • 아까 본 dependent binary pixel image에 chain rule을 적용하면 똑같이 parameter가 $2^n - 1$개 필요함을 확인할 수 있다.
2. Bayes’ rule $$ P(x \vert y) = \dfrac{p(x, y)}{p(y)} = \dfrac{P(y \vert x) p(x)}{P(y)} $$
   • 베이즈 정리는 이전에 이미 배운 적이 있다.
3. Conditional Independence $$ \text{If} \;\; x \perp y \vert z, \;\;\text{then} \;\;\; p(x \vert y, z) = p(x \vert z) $$
   • $\perp$는 독립을 의미한다. 즉, $z$가 주어졌을 때 $x$와 $y$가 서로 독립이 되면 이 때 $y$의 발생여부는 상관 없으니까 없애도 된다는 뜻이다.

우리가 찾고자 하는 것은, 학습시킬 수 있는 적당한 parameter를 가진 확률분포이다.

Markov assumption($i+1$번째 픽셀은 $i$번째 픽셀에만 dependent한 경우)에서는 다음이 성립한다.

$$ p(x_1, \cdots, x_{n}) = p(x_1)p(x_2 \vert x_1)p(x _3 \vert x _2) \cdots p(x_n \vert x_{n - 1}) $$

따라서 이 때 필요한 parameter는 $p(x_1)$, $p(x_2 \vert x_1 = 0)$, $p(x_2 \vert x_1 = 1)$, $p(x_3 \vert x_2 = 0)$, $p(x_3 \vert x_2 = 1)$, $\cdots$, $p(x_n \vert x_{n-1} = 0)$, $p(x_{n} \vert x_{n-1} = 1)$으로 총 $2n - 1$개이다.

따라서 이러한 가정 안에서는 parameter 개수가 대폭 줄어들게 되며, 이러한 조건부 독립성을 이용한 모델이 바로 Auto-regressive model(AR model)이다.

참고로, 위에서 가정한 것은 AR-1 model에 속하며, 이것은 현재의 확률이 단순히 이전 1개에만 dependent한 경우이다. 이전 $n$개에 dependent한(즉, $n$개를 고려하는) 모델을 AR-n 모델이라고 부른다. 그리고 사실 어떤 식으로 conditional independence를 주느냐에 따라 각 픽셀이 dependent 변수의 개수가 다를수도 있으므로, 이를 조절하는 것이 모델 자체에 큰 영향을 준다. 따라서 이런 conditional independence를 잘 부여하는 것이 중요하다.

Auto regressive Model (AR model)

위에서 보았던 28 x 28 이미지의 joint distribution을 chain rule으로 나타내면 아래와 같다.

$$ p(x_{1:784}) = p(x_1)p(x_2 \vert x_1)p(x_3 \vert x_{1:2}) \cdots $$

여기서 conditional independence를 어느정도 부여하게 되는데, 이러면 앞서 살펴본 3번 rule에 따라 해당 변수를 확률 식에서 지울 수 있으므로 그 부분의 필요 파라미터 개수를 줄일 수 있다.

참고로 위에서 말한 ‘이전 픽셀’이라는게 픽셀들을 순서대로 나열한 이후에 정의될 수 있는데, 이 순서를 정하는 방법에도 여러가지가 있다. 그리고 당연히 순서를 정하는 방법론도 모델의 구조나 성능에 많은 영향을 준다.

AR model에는 아래와 같은 모델이 존재한다.

• NADE(Neural Autoregressive Density Estimator)
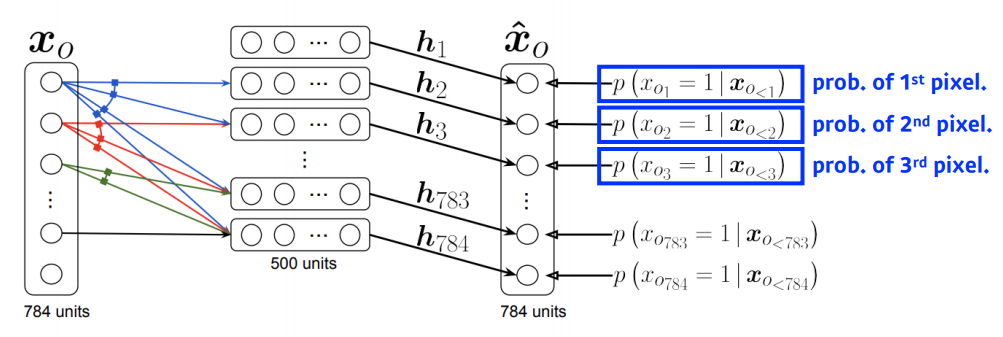
  • $i$번째 픽셀이 $1$번째부터 $i-1$번째까지 픽셀에 모두 dependent한 모델이다.
  $$ p(x_i \vert x _ {1:i-1}) = \sigma (\alpha _i \mathrm{h}_i + b_i) $$ $$ \mathrm{h}_i = \alpha (W _{< i} x_{1:i-1} + c) $$
  • 위 식을 말로 표현해보자.
    1. $i$번째 conditional probability를 구하고자 한다.
    2. $1 \sim i - 1$번째 값을 affine layer에 통과시킨 값을 시그모이드에 통과시켜 $\mathrm{h}_i$를 얻는다.
    3. 그 값을 다시 어떤 값 $\alpha$에 곱해서 시그모이드를 한번 더 통과시킨 값이 확률이 된다.
  • $1 \sim i - 1$번째 확률을 다 고려한다는 점, 그리고 input이 아래로 갈수록 늘어나니까 affine layer에서 곱해주는 가중치의 dimension도 올라간다는 점 정도를 생각해보면 될 것 같다.
    • 예를 들어 $x_{58}$에 대한 확률을 구하려고 하면 57개의 input을 받을 수 있는 가중치 $W$가 필요할 것이다.
  • NADE는 explicit 모델로, 784개 입력에 대한 확률 계산이 가능하다. $$ p(x_1, \cdots, x_784) = p(x_1)p(x_2 \vert x_1) \cdots p(x_{784} \vert x_{1:783}) $$
    • 각 $p(x_i \vert x _ {1:i-1})$는 독립적으로 앞에서 계산되었으니까 이것으로 특정상황에 대한 확률 계산이 가능하다.
  • 지금까지 계속 discrete variable에 대해서만 다루었는데, 만약 continuous variable을 다루고 싶다면 a mixture of Gaussian 분포를 사용하면 된다.
  • 장황하게 써놨는데.. $\alpha$가 무슨 값을 지칭하는지도 모르겠고, 이거 포함해서 아직 이걸 정확히 이해한건 아니다. 하지만 검색해도 정보가 많이 없고 수업에서도 비중을 적게 한걸로 봐선 굳이 더 자세히 찾아보진 않으려고 한다.
  • 여담으로, 이 모델처럼 density estimator라는 이름이 붙은 모델은 explicit model이라고 보면 된다. 단어부터 그런 뉘앙스를 준다.
• Pixel RNN
  • RNN을 사용하여 정의된 AR model이다.
  • 예를 들어, n x n 이미지의 RGB를 나타내면 아래와 같다.
  $$ p(x) = \prod\limits _{i=1}^{n^2} p(x_{i,R} \vert x_{<i})p(x_{i,G} \vert x_{<i},x_{i,R})p(x_{i,B} \vert x_{<i},x_{i,R},x_{i,G}) $$
  • 지금까지 들어온 픽셀을 기반으로 다음 픽셀을 예측(RNN 관점) 혹은 생성(AR model 관점)한다.
  • RNN에서도 과거의 정보를 고려하니까 이러한 특성을 generative model을 쓸 때도 적용할 수 있는 것 같다.
    • 즉, 픽셀의 sequence를 그냥 픽셀이 쭉 이어져있는 시계열 데이터라고 보는 것이다.
  • 가장 고전적인 Pixel RNN은 말그대로 픽셀 sequence를 쭉 펴서 RNN처럼 돌린다.
  • 그런데 앞서 말했듯이, generative model에서는 순서를 정하는 방법도 중요한데, 이에 따라 아래와 같이 두 개의 모델이 나오게 된다.
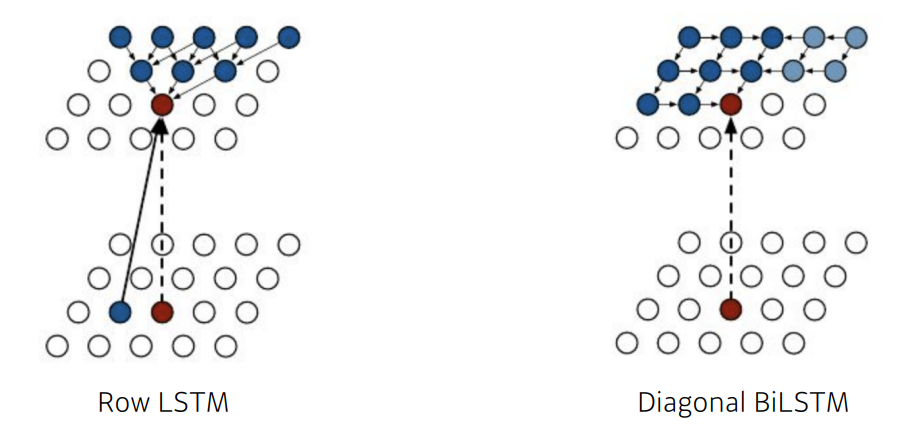
    • 둘다 LSTM 구조를 기반으로 한다.
    • Row LSTM은 모든 픽셀을 보지 않고 직접적인 영향을 주는 픽셀(위쪽 triangular)들을 통해서만 학습한다. 근데 바로 옆 pixel도 영향을 줄 수 있으니까 이것까지 고려한다.
    • Diagnoal BiLSTM은 지금까지 들어온 이전 모든 정보를 활용하여 학습한다. 고전적인 RNN에서는 오른쪽에서 오는 픽셀 정보를 고려하기가 쉽지 않다고 하는데, 이 점을 개선한 것 같다.
    • Diagonal BiLSTM이 연산량이 더 많지만 빠르고, 반대로 Row LSTM은 연산량이 적다는 이점이 있다.

Variational Auto-Encoder, VAE

Reference로 달아둔 영상들을 꼭 다시 보도록 하자.
내용이 방대하고 어려워 모든 것을 자세히 쓰지는 않았고, 여기서는 수식을 통해 전체적인 흐름을 자연스럽게 따라가는 것을 목표로 한다.

Autoencoder

Autoencoder를 알기 위해서는 먼저 manifold에 대해 알아야 한다. manifold란 고차원 데이터를 데이터 공간에 뿌렸을 때 그 데이터 전체를 잘 아우르는 subspace를 뜻한다. 즉 데이터 전체의 분포를 나타내는 하나의 벡터공간이라고 보면 될 것 같다.

Autoencoder는 결론부터 말하면 데이터 압축과 데이터의 중요한 feature들을 찾아내는데에 큰 역할을 한다.

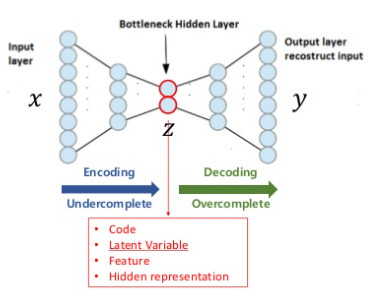
Reference의 이활석님 오토인코더 강의中

여기서는 $x$라는 데이터를 입력으로 넣으면 $x$라는 데이터가 출력으로 그대로 나오기를 기대한다. 여기서 가운데에 $\mathrm{z}$라는 latent vector가 우리가 추출하고자하는 축소된 데이터이다. 우리는 손실함수 $L(x, y)$를 최소화함으로써 쉽게 학습할 수 있다. 여기서 $x$는 입력값, $y$는 출력값인데 결국 입력과 출력이 같기를 원하고 있으므로 손실함수를 이렇게 설정할 수 있다.

그냥 직관적으로 보면, $x$가 Encoder를 거쳐 $\mathrm{z}$ 벡터가 되었고 Decoder를 통해 그 벡터가 원상복구되었다. 그렇다면 $\mathrm{z}$가 $x$를 축소한 것이라고 이해할 수 있다. 이를 통해 우리는 autoencoder가 결국은 training data의 manifold를 학습한다고 이해할 수 있다.

manifold를 구하는 방법에는 사실 여러가지가 있지만, 대부분 K-최근접 이웃 기법을 사용하기 때문에 고차원 벡터를 축소시킬 때 자연스럽게 유클리드 거리를 사용하게 된다.

하지만 2차원, 3차원에서 더 나아가 매우 고차원이 되면 단순히 유클리드 거리만으로 manifold를 찾는건 오류가 생길 가능성이 크다.
예를 들어, 실제 manifold가 빙글빙글 꼬여있는 상태라고 생각해보면 유클리드 거리로 이웃을 찾았을 때 그 이웃은 실제 manifold 위에 없을 가능성이 크다.

그래서 고차원 데이터일수록 autoencoder를 사용하는 것이 manifold를 찾는 데에 더 유리하며, 특히 autoencoder는 신경망 구조를 채택하기 때문에 데이터의 양이 많을수록 더 성능이 좋다는 장점도 있다.

Variational Auto-encoder

근데 사실 위에서 설명한 general autoencoder는 generative model은 아니다. 어디까지나 차원축소를 하고 그 축소된 벡터들의 manifold를 구하는 데에는 도움이 될 수 있겠지만, 무언가 새로운 것을 생성하는 것은 아니다. (latent vector $\mathrm{z}$는 생성된거라기보다는, 그냥 $x$가 축소된 것이다)

그래서 VAE라는 컨셉이 등장하게된다. 이것은 generative model로 입력 $x$와 비슷한 무언가를 생성해내는것이 목적이다.

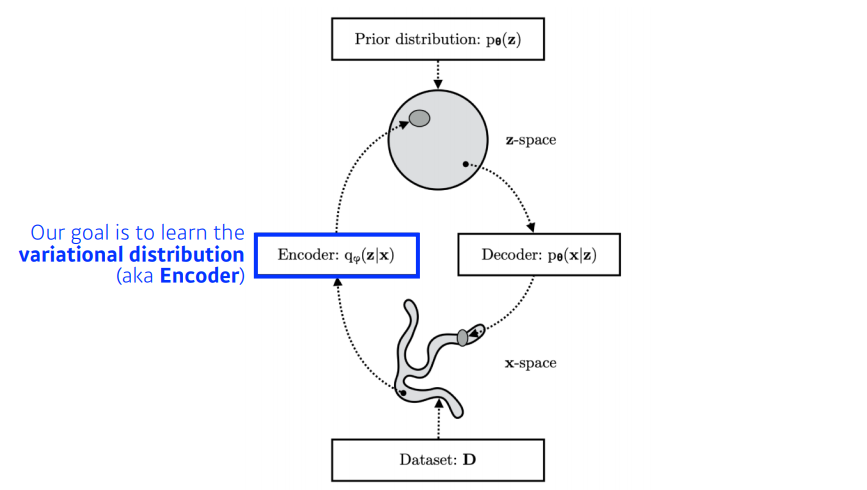
그런데 일단 무언가 생성을 하려면 $x$를 만들 수 있는 latent vector $\mathrm{z}$의 분포를 알아야한다. 즉, latent space를 찾아야 한다. 만약 latent vector의 분포(latent space)를 알게되면 그 분포에서 무언가를 샘플링해서 모델에 넣으면 $x$와 비슷한 출력이 나오게 될 것이다.

문제는 그 샘플링 함수를 우리는 모른다. 데이터가 매우 많고 고차원이기 때문에 이 분포를 찾거나 이 분포를 따르는 새로운 데이터를 만드는 것이 쉽지 않다. 그래서 여기서 우리는 일단 $x$가 주어졌을 때 latent vector $\mathrm{z}$의 분포를 우리가 잘 알고 있는 정규분포 $\mathrm{z} \sim \mathscr{N} (0, 1)$로 표현하고자 한다. 정규분포는 평균과 표준편차만 찾는다면 그 형태를 표현할 수 있다.

먼저 Encoder는 들어온 데이터의 평균과 표준편차를 출력할 것이다. 이후 이를 따르는 정규분포에서 새로운 잠재변수 $\mathrm{z}$를 샘플링한다. 잠재벡터는 디코더를 거쳐 새로운 데이터를 생성할 것이다.

이를 위해 Variance Inference(VI) 방법을 사용한다.

먼저 데이터 $x$가 주어졌을 때의 $\mathrm{z}$의 확률분포는 posterior distribution으로 $p _{\theta} (\mathrm{z} \vert x)$로 표기한다. 그리고 이에 근사하는 variational distribution $q _{\theta} (\mathrm{z} \vert x)$를 찾는 것이 우리의 목표이다. 이제 주어진 샘플 $x$의 분포를 한 번 잘 표현해보자.

$$ p _{\theta} (\mathrm{z} \vert x) \approx q _{\theta} (\mathrm{z} \vert x) \sim \mathrm{z} $$

그러면 이제 posterior distribution $p _{\theta} (\mathrm{z} \vert x)$과 variational distribution $q _{\theta} (\mathrm{z} \vert x)$ 간의 관계식을 찾아야한다. 이 관계식으로부터 무언가 할 수 있는게 있다면 목표하는 확률분포를 찾을 수 있을 것이다. 그렇게 나타나게 된 식이 아래와 같다.

$$ \begin{aligned} \ln p_{\theta}(D) &=\int log(p(x)) q_\phi (\mathrm{z} \vert x) d \mathrm{z} \;\;\;\;\;\; \leftarrow \int q_\phi (\mathrm{z} \vert x) d \mathrm{z} = 1 \\ &=\int \log{\left( \dfrac{p(x, \mathrm{z})}{p(\mathrm{z} \vert x)} \right)} q _\phi (\mathrm{z} \vert x)d \mathrm{z} \;\;\;\;\;\; \leftarrow p(x) = \dfrac{p(x, \mathrm{z})}{p(\mathrm{z} \vert x)}\\ &=\int \log{\left( \dfrac{p(x, \mathrm{z})}{q _\phi (\mathrm{z} \vert x)} \cdot \dfrac{q _\phi (\mathrm{z} \vert x)}{p(\mathrm{z} \vert x)} \right)} q _\phi (\mathrm{z} \vert x)d \mathrm{z} \\ &=\underbrace{\int \log{\left( \dfrac{p(x, \mathrm{z})}{q _\phi (\mathrm{z} \vert x)} \right)} q _\phi (\mathrm{z} \vert x)d \mathrm{z}}_{\text {ELBO}(\phi) }+\underbrace{\int \log{\left( \dfrac{q _\phi (\mathrm{z} \vert x)}{p(\mathrm{z} \vert x)} \right)} q _\phi (\mathrm{z} \vert x)d \mathrm{z}}_{ KL\left( q _{\phi} (\mathrm{z} \vert x \Vert p( \mathrm{z} \vert x) ) \right) } \end{aligned} $$

강의에서는 위 식을 아래와 같이 표현하였는데, 결국 continuous distribution에서 기댓값은 곧 적분값이기 때문에 사실 같은 표현이라고 보면 된다. 다만 개인적으로는 위 식이 더 이해하기 편해서 식을 위와 같이 썼다.

$$ \begin{aligned} \ln p_{\theta}(D) &=\mathbb{E}_{q_{\phi}(\mathrm{z} \vert x)}\left[\ln p_{\theta}(x)\right] \\ &=\mathbb{E}_{q_{\phi}(\mathrm{z} \vert x)}\left[\ln \frac{p_{\theta}(x, \mathrm{z})}{p_{\theta}(\mathrm{z} \vert x)}\right] \\ &=\mathbb{E}_{q_{\phi}(\mathrm{z} \vert x)}\left[\ln \frac{p_{\theta}(x, \mathrm{z}) q_{\phi}(\mathrm{z} \vert x)}{q_{\phi}(\mathrm{z} \vert x) p_{\theta}(\mathrm{z} \vert x)}\right] \\ &=\mathbb{E}_{q_{\phi}(\mathrm{z} \vert x)}\left[\ln \frac{p_{\theta}(x, \mathrm{z})}{q_{\phi}(\mathrm{z} \vert x)}\right]+\mathbb{E}_{q_{\phi}(\mathrm{z} \vert x)}\left[\ln \frac{q_{\phi}(\mathrm{z} \vert x)}{p_{\theta}(\mathrm{z} \vert x)}\right] \\ &=\underbrace{\mathbb{E}_{q_{\phi}(\mathrm{z} \vert x)}\left[\ln \frac{p_{\theta}(x, \mathrm{z})}{q_{\phi}(\mathrm{z} \vert x)}\right]}_{\text {ELBO } \uparrow}+\underbrace{D_{K L}\left(q_{\phi}(\mathrm{z} \vert x) \| p_{\theta}(\mathrm{z} \vert x)\right)}_{\text {Objective } \downarrow} \end{aligned} $$

$p _{\theta} (\mathrm{z} \vert x)$과 $q _{\theta} (\mathrm{z} \vert x)$ 간의 거리(KL-Divergence)는 두번째 항이다. 그런데 두번째 항에는 $x$가 포함되어있는 $p _\theta (\mathrm{z} \vert x)$이 포함되어있다. 이 항은 $x$의 분포가 매우 복잡하기 때문에 알 수 없다고 앞에서 언급하였다. 그래서 우리는 그 항을 최소화해야하는데 그 값을 알 수 없다. 따라서 두번째 항을 최소화하기 위해 첫번째 항을 최대화하는 방법을 취한다.

첫번째 항은 ELBO(Evidence Lower Bound)를 뜻하는데, 이를 maximization하는 $\underset{\phi}{\mathrm{argmax}} \; ELBO (\phi)$를 찾아야한다. 다시 ELBO term을 풀어서 전개해보면

$$ \begin{aligned} ELBO(\phi) &=\int \log{\left( \dfrac{p(x, \mathrm{z})}{q _\phi (\mathrm{z} \vert x)} \right)} q _\phi (\mathrm{z} \vert x)d \mathrm{z} \\ &=\int \log{\left( \dfrac{p(x \vert \mathrm{z}) p(z)}{q _\phi (\mathrm{z} \vert x)} \right)} q _\phi (\mathrm{z} \vert x)d \mathrm{z} \\ &=\int \log{(p(x \vert \mathrm{z}))} q _\phi (\mathrm{z} \vert x)d \mathrm{z} - \int \log{\left( \dfrac{q _\phi (\mathrm{z} \vert x)}{p(\mathrm{z})} \right) q _\phi (\mathrm{z} \vert x)d \mathrm{z}} \\ &=\underbrace{\mathbb{E}_{q_{\phi}(\mathrm{z} \vert x)} \left[\log{(p(x \vert \mathrm{z}))}\right]}_{\text{Reconstruction Term}} - \underbrace{KL(q _\phi (\mathrm{z} \vert x) \Vert p(\mathrm{z}))}_{\text{Prior Fitting Term}} \end{aligned} $$

참고로, 두번째 항은 앞의 KL 항과 인자가 다르다. (결론부터 말하면 이건 계산이 가능하다)

첫번째 항은 decoder가 $\mathrm{z}$를 $x$로 만드는 확률분포 $p _\theta (x \vert \mathrm{z})$과 같고, 이것 역시 maximize해야하므로 첫번째 항을 maximize하는 것은 결국 decoder의 $p _\theta (x \vert \mathrm{z})$을 maximize하는 것과 같다. (Maximum Likelihood Estimation(MLE)을 하는 것과 동일)

정리하면, $x$가 나타날 확률을 계산하는 것은 우리가 가지고 있는 샘플들에 대한 확률 분포를 찾고자 하는 것이고, 지금 하고자 하는 것은 $\mathrm{z}$로부터 $x$가 나타날 확률을 최대화하는 것이므로 결국 MLE를 사용하는 것과 같다.

한편 두번째 항의 경우, 같은 Restruction Error을 가진 $q _\phi$가 여러개 있다면 기왕이면 Prior와 같은 모양이 되었으면 좋겠다라는 점을 반영한 항이다.

지금까지만 봐도, VAE랑 AE는 형태는 비슷하게 생겼지만 수학적으로 보았을때 아예 다른 관점으로 돌아가는 모델이다.

이제 이것의 최대를 구해보자.

Reconstruction 항의 경우, 기댓값이므로 적분을 해야겠지만 여러번 반복 샘플링하여 Monte-carlo technique으로 적분에 근사하는 값을 구하면 된다.

$$ \begin{aligned} \mathbb{E}_{q_{\phi}(\mathrm{z} \vert x _i)} \left[\log{(p _\theta (x _i \vert \mathrm{z}))}\right] &= \int \log{\left( p _\theta (x _i \vert \mathrm{z}) \right)} q _\phi (\mathrm{z} \vert x_i ) d \mathrm {z} \\ &\approx \dfrac{1}{L} \sum\nolimits _{z ^{i, l}} \log \left( p _\theta (x _i \vert \mathrm{z} ^ {i, l}) \right) \end{aligned} $$

그래서 결국 계산해보면 Reconstruction error는 cross-entropy 형태로 나오게 된다.

$$ \mathbb{E}_{q_{\phi}(\mathrm{z} \vert x)} \left[\log{(p(x \vert \mathrm{z}))}\right] \\ = \sum _i x_i \log(\text{Decode}(\text{Encode}(x_i))) + (1-x_i) \log(1 - \text{Decode}(\text{Encode}(x_i))) \\ = \sum _i x_i \log{\hat{x_i}} + (1- x_i) \log(1- \hat{x_i}) $$

이제 두번째 항(KL Divergence 항)을 보자. 참고로, KL Divergence는 확률분포 두 개가 모두 Gaussian distribution을 따를 때 간소화하여 계산하는 방법이 이미 알려져있다. 근데 마침 해당 항에 표현된 두 확률분포가 모두 가우시안 분포를 따른다!

$p(\mathrm{z})$는 앞서 Gaussian distribution을 따르는 것으로 가정하였다. $q _\phi (\mathrm{z} \vert x)$ 또한 $\mathrm{z}$가 정규 분포를 따르므로 정규 분포를 따른다.

$$ \mathrm{z} \sim \mathscr{N} (0, 1) \\ q _\phi (\mathrm{z} \vert x) \sim \mathscr{N} (\mu _{\mathrm{z}_i}, \sigma _{\mathrm{z}_i}) $$

이를 반영하면 계산 결과는 다음과 같다.

$$ D_{K L}\left(q_{\phi}(\mathrm{z} \vert x) \| \mathcal{N}(0, 1)\right)=\frac{1}{2} \sum_{i=1}^{D}\left(\sigma_{\mathrm{z}_{i}}^{2}+\mu_{\mathrm{z}_{i}}^{2}-\ln \left(\sigma_{\mathrm{z}_{i}}^{2}\right)-1\right) $$

이렇게해서 원하는 분포에 근사할 수 있도록 하는 방법을 알 수 있게 되었다.

그런데 $\mathrm{z}$를 샘플링을 하는 과정이 구해진 분포에서 그냥 random으로 하게 되면 backpropagation algorithm을 사용할 수가 없다. (encoder의 파라미터와 샘플링된 $\mathrm{z}$간의 연결관계를 찾을 수 없다.) 논문에서는 reparameterization trick을 써서 이에 대한 문제를 해결하였다. 계산된 분포 $\mathscr{N}(\mu, \sigma)$에 epsilon $\epsilon$을 더하는 방식으로 $\mathrm{z}$를 샘플링하면 추후 학습 시 $\mathrm{z}$가 encoder의 parameter에 영향을 미치는 관계를 찾아갈 수 있다. 이 트릭에 대한 자세한 과정은 여기서는 생략한다.

아직 완벽히 이해가 된 것은 아니지만, 전체적 흐름은 익혔고 더이상 파고들기엔 아직 지식이 부족하기 때문에 VAE는 여기까지만 기술하려고한다.

그 외에 AAE(Adversarial Auto-encoder)라는 변형 VAE모델도 있다.

앞서 나온 VAE는 latent space를 가우시안 분포로 가정하였는데, 실제로는 가우시안 분포로 하였을 때 오차가 크게 발생할 수도 있다. 이를 위해 이 모델에서는 adversarial autoencoder를 사용하여 latent distribution과 가우시안 분포 사이의 오차를 최소화해준다.

Generative Adversarial Network, GAN

Reference로 달아둔 영상들을 꼭 다시 보도록 하자.
VAE에 대한 내용과 동일하게, 여기서는 수식을 통해 자연스럽게 흘러가는 흐름을 짚어보도록 하자.

GAN는 흔히 적대적 학습이라고 알려진 유명한 모델이다.
크게 보면 Discriminator, Generator로 이루어져있으며 두 장치가 서로를 속이려고 학습하고, 안 속으려고 학습하는 과정을 반복하여 원하는 generator를 형성하는 것이 목표이다. 이를 통해 unsupervised learning이 자연스럽게 이루어진다.

Generative Adversarial Network

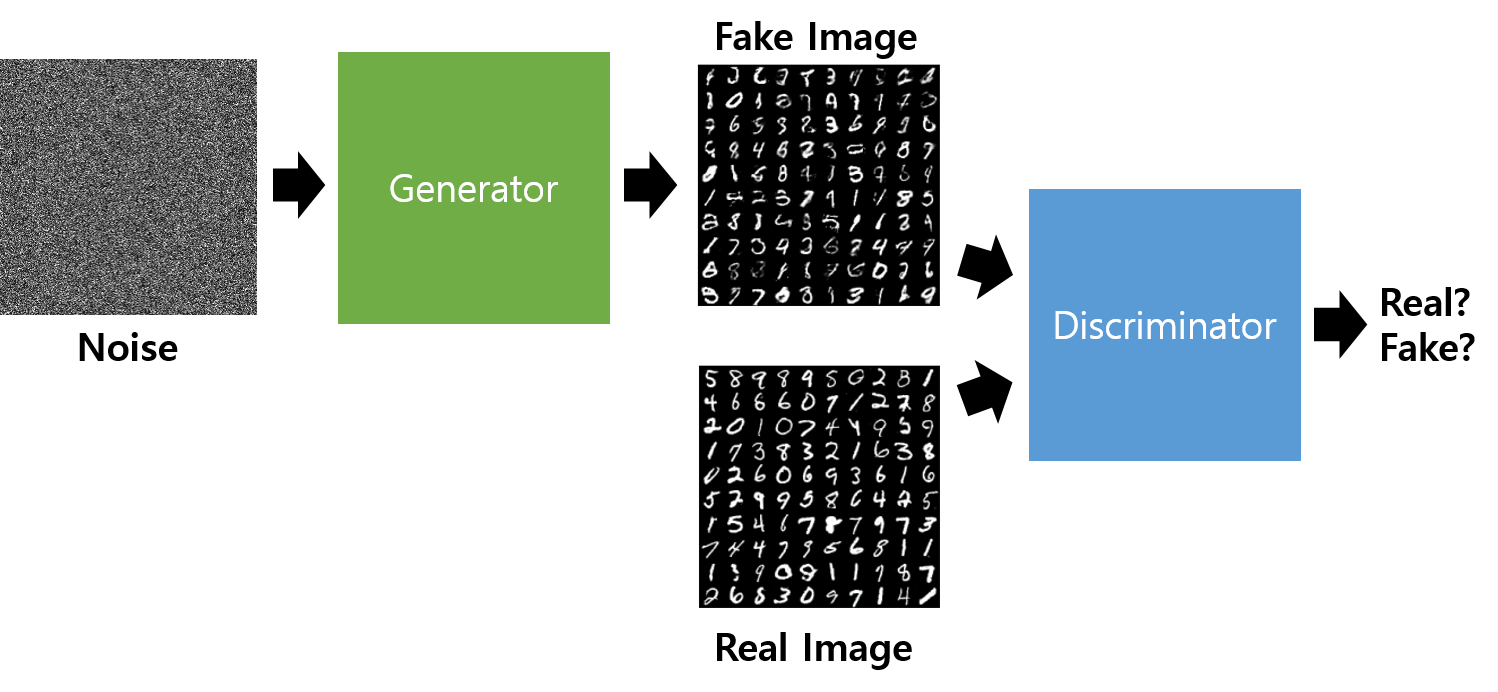
• Discriminator는 들어온 image에 대하여 fake image이면 0을, real image이면 1을 출력한다.
• Generator는 discriminator가 1을 출력하도록 이미지를 만든다.

이를 Discriminator 입장에서의 수식으로 표현하면 다음과 같다.

$$ \text{Loss} _D = \text{Error}(D(x),1) + \text{Error}(D(G(\mathrm{z})),0) $$

$D(x)$는 Discriminator로, real data $x$를 받으면 1을 출력하기를 원한다.
또한 $G(z)$는 Generator가 latent vector $\mathrm{z}$를 받았을 때 생성하는 값이다.
따라서 Discriminator 입장에서는 $D(G(z))$가 0이기를 바란다.

한편, Generator 입장에서는 $D(G(z))$가 0이기를 바란다. Real image를 discriminator가 0으로 판단하든, 1로 판단하든 generator는 관심이 없기 때문에 관련 항은 존재하지 않는다.

$$ \text{Loss} _G = \text{Error}(D(G(\mathrm{z})),1) $$

결과가 binomial 값이기 때문에 결국 이를 cross entropy error 식으로 표현할 수 있으며 이는 다음과 같다.

$$ \text{CEE} = -q \log(p) - (1-q) \log(1-p) \\ \text{Loss} _D = -\log(D(x)) -\log(1-D(G(\mathrm{z}))) \\ \text{Loss} _G = -\log(D(G(\mathrm{z}))) $$

이제 위 식을 최소화하면 된다.

실제 논문에서는 D에 대한 loss를 최대화하고, G에 대한 loss를 최소화하는 방향으로 식을 합쳤다. 그 결과 다음과 같은 식이 나온다.

$$ \min_ G \max_ D V(D, G) = \mathbb{E} _{x \sim p_{\text{data}}(x)} \left[ \log D(x) \right] + \mathbb{E} _{\mathrm{z} \sim p_{\mathrm{z}}(z)} \left[ \log(1 - D(G(\mathrm{z}))) \right] $$

여기서도 latent vector $\mathrm{z}$는 Gaussian distribution을 따른다고 가정한다. Discriminator는 우변의 두 항 모두를 maximize 하기를 원한다. 다만 우변 첫번째 식은 Genertor와 관련이 없기 때문에 Generator 즉 $\min_G$는 우변 두번째 식을 최소화하는 것에만 관심이 있다.

기댓값은 적분이고, 이를 discriminator 입장에서 최대화하기 위해서는 미분을 통해 극점을 찾아야 한다.

$$ \begin{aligned} \min_ G \max_ D V(D, G) &= \mathbb{E} _{x \sim p_{\text{data}}(x)} \left[ \log D(x) \right] + \mathbb{E} _{\mathrm{z} \sim p_{\mathrm{z}}(z)} \left[ \log(1 - D(G(\mathrm{z}))) \right] \\ &= \int \left[ P _{x \sim p_{\text{data}}(x)} x \log D(x) + P _{x \sim p_{G}(x)} x \log (1 - D(x)) \right] dx \end{aligned} $$
$$ \partial _D \min_ G \max_ D V(D, G) = P _{x \sim p_{\text{data}}(x)} x \log D(x) + P _{x \sim p_{G}(x)} x \log (1 - D(x)) = 0 $$

이를 풀기 위해 아래 식을 이용하면,

$$ y = a \log(y) + b \log(1-y) $$ $$ y ^\prime = \dfrac{a}{y} - \dfrac{b}{1-y} = 0 $$ $$ y ^{*} = \dfrac{a}{a + b} $$

결국

$$ D ^{*} _G (x) = \dfrac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_{G}(x)} $$

이 된다.

지금까지 discriminator가 원하는 값을 최대화하기위한 수식을 살펴보았다. 우리의 목표는 generator가 discriminator를 속일 수 있도록 학습시키는 것이다. 이제 generator 입장에서 위 discriminator의 수식을 대입해보면,

$$ V(G, D ^{*} _G (x)) = \int \left( \mathbb{E} _{x \sim p_{\text{data}}(x)} \left[ \log \left( \dfrac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_{G}(x)} \right) \right] \\ \hspace{3cm} + \mathbb{E} _{\mathrm{z} \sim p_{\mathrm{z}}(z)} \left[ \log \left(\dfrac{p_G (x)}{p_{\text{data}}(x) + p_{G}(x)} \right) \right] \right) dx \\ = \int \left( \mathbb{E} _{x \sim p_{\text{data}}(x)} \left[ \log \left( \dfrac{p_{\text{data}}(x)}{\frac{p_{\text{data}}(x) + p_{G}(x)}{2}} \right) \right] \\ \hspace{4cm} + \mathbb{E} _{\mathrm{z} \sim p_{\mathrm{z}}(z)} \left[ \log \left(\dfrac{p_G (x)}{\frac{p_{\text{data}}(x) + p_{G}(x)}{2}} \right) \right] \right) dx - \log 4 \\ = \underbrace{D_{\text{KL}} \left[ p_{\text{data}}, \; \frac{p_{\text{data}} + p_{G}}{2} \right] + D_{\text{KL}} \left[ p_G, \; \frac{p_{\text{data}} + p_{G}}{2} \right]}_{2 \times \text{Jenson-Shannon Divergence (JSD)}} - \log 4 \\ = 2D_{\text{JSD}} \left[ p_{\text{data}}, p_G \right] - \log 4 $$

따라서 $V$가 최소가 되는 경우는 $D_{\text{JSD}} = 0$ 즉 $p=q$인 경우이다. (원래 데이터의 확률 분포와 Generator의 확률 분포가 같은 경우) 이 경우 $D ^{*} _G (x) = \frac{1}{2}$이고 $V(D, G) = -2\log 2$가 된다. 따라서 generator는 $D_{\text{JSD}} = 0$이 되도록 학습을 진행하게 된다.

다만 이 방법은 보다시피 discriminator의 학습 방향을 고정시켜놓고 찾은 값이다. 실제로는, discriminator와 generator가 함께 학습을 하기 때문에 위 과정은 이론적인 이야기이고 실제 모델링은 조금 상이할 것으로 예상된다.

GAN 모델은 기존의 VAE 등의 모델보다 훨씬 정확한 학습을 할 수 있다. 또한 확률 input의 확률 모델을 명확하게 정의하지 않아도 동작이 가능하다. 다만 여전히 평가의 기준을 세우기 애매하여 사람이 직접 그림을 보고 판단해야한다는 한계점이 존재한다.

실제 구현과 논문의 차이점

$$ \min_ G \max_ D V(D, G) = \mathbb{E} _{x \sim p_{\text{data}}(x)} \left[ \log D(x) \right] + \mathbb{E} _{\mathrm{z} \sim p_{\mathrm{z}}(z)} \left[ \log(1 - D(G(\mathrm{z}))) \right] $$

위 식은 아까 본 Loss 식과 똑같다. 그런데 우변 두번째 식이 사실 Generator 입장에서 학습할 때 미분을 하게 되는데 저 상태 그대로 미분하면 기울기가 상대적으로 낮아 학습이 빠르게 되지 않는다.

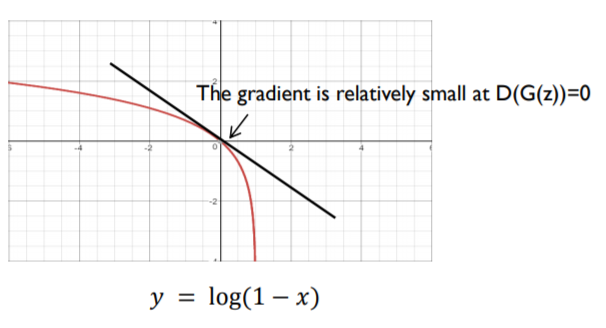
Reference의 최윤제님 GAN 강의中

처음 학습할때는 당연히 generator는 전혀 엉뚱한 이미지를 생성하게 될텐데, 이러면 generator의 학습이 빠르게 되지 않는 이상 discriminator가 압도적으로 빠르게 학습될 가능성이 있다. 따라서 실제 구현에서는 다음과 같이 식을 변경하여 사용한다.

$$ \min_ G \mathbb{E} _{\mathrm{z} \sim p_{\mathrm{z}}(z)} \left[ \log(1 - D(G(\mathrm{z}))) \right] \rightarrow \max_ G \mathbb{E} _{\mathrm{z} \sim p_{\mathrm{z}}(z)} \left[ \log(D(G(\mathrm{z}))) \right] $$

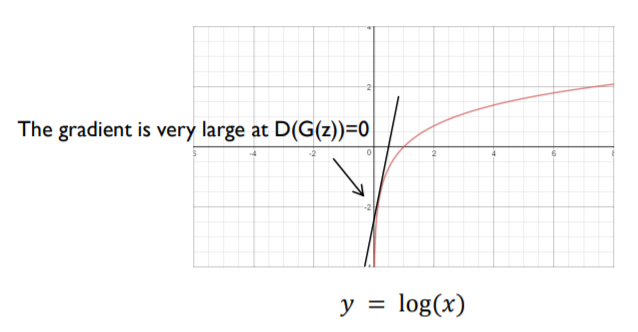
Reference의 최윤제님 GAN 강의中

지향점은 같으나 실제 구현에서 더 좋은 성능을 내기 위해 위와 같이 구현한다.

GAN 변형 모델

• DCGAN
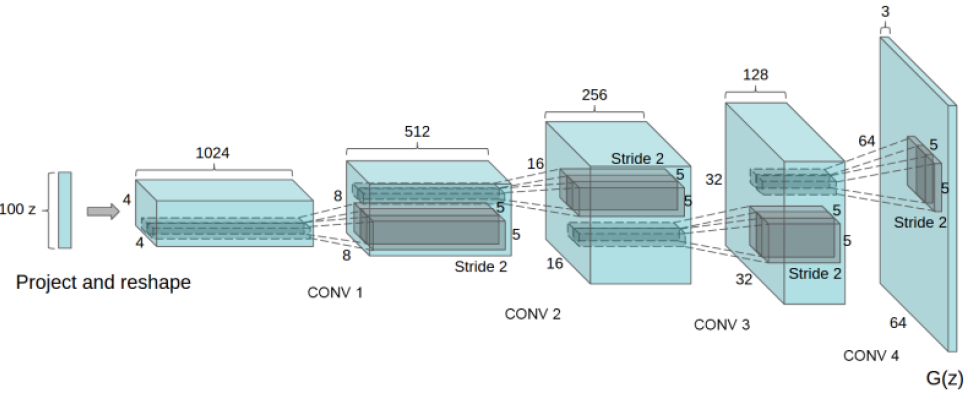
  • CNN을 활용한 GAN 모델이다.
  • 기존 GAN에서는 affine layer를 사용한 반면, DCGAN은 Convolution layer를 사용하며, Generator는 Deconvolution을 사용한다.
  • DCGAN에서는 이미지가 블럭화되는 현상을 막기 위해 pooling layer를 사용하지 않고 stride size가 2이상인 convolution/deconvolution을 사용한다.
  • 학습 안정을 위해 batch normalization / Adam optimzer을 사용한다.
• InfoGAN
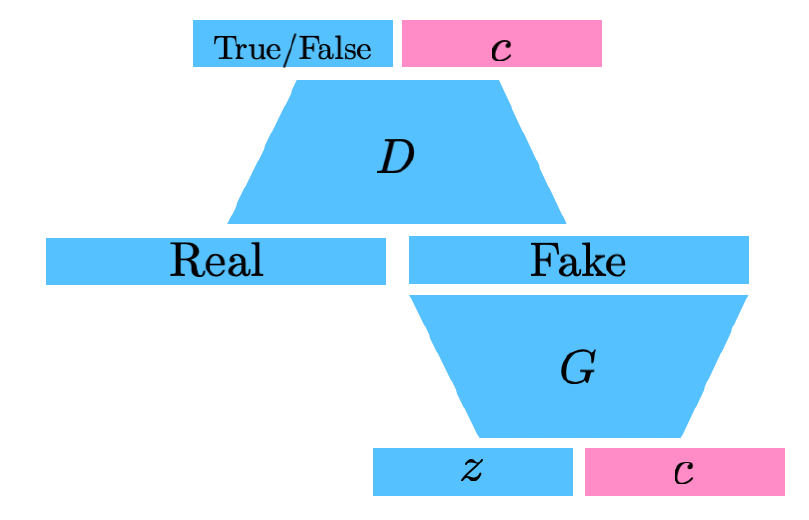
  • input으로 $\mathrm{z}$뿐만 아니라, code라는 latent variable $\mathrm{c}$를 추가로 함께 넣어준다.
  • 무언가 생성할 시 GAN이 특정 특징분포에 집중할 수 있도록 만들어준다.
  • 예를 들어 MNIST에서는 $\mathrm{c}$를 넣어줌으로써 글씨의 두께, 글씨의 기울기 등을 변화시킬 수 있다.
• Text2Image
  • 문장이 주어지면 해당 문장에 맞는 이미지를 만들어내는 연구에 대한 논문이다.
  • 최근에 DALL-E 모델이 발표되었는데, 이 모델 역시 Text2Image 컨셉의 모델로 성능이 뛰어나다고 한다. 다만 이 모델은 Transformer에 기반한 모델이다.
  • Input이 문장이고 이를 통해 이미지 output을 내놓기 때문에 모델이 매우 복잡하다.
• CycleGAN

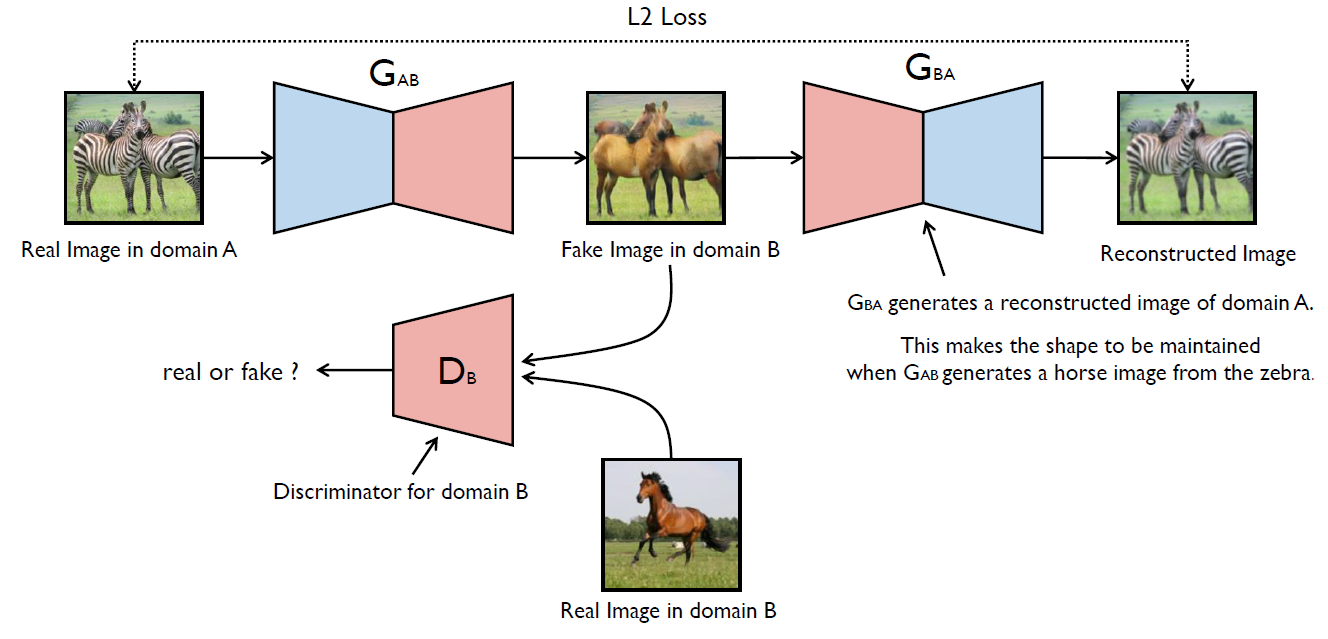
  Reference의 최윤제님 GAN 강의中

  • 이미지의 domain/style을 바꾸는 GAN이다. 따라서 generator는 latent vector가 아닌 image 자체를 받게 된다.
  • 서로 다른 두 GAN 네트워크를 주고, 뒷 부분 GAN은 Fake Image를 Real Image로 다시 돌리는 역할을 한다. (Cycle 느낌)
    • 만약 GAN이 하나만 있다면 generator는 discriminator를 속이기 위해 얼룩말의 형체를 유지하지 않고 말 사진을 생성하려고 할 것이다.
    • GAN이 2개 있으면 맨 끝에 다시 복원된 이미지가 원래 이미지와 같아야 하기 때문에(이 두 개가 Loss의 기준) 모양을 유지하려고 한다.
  • 여기서 사용된 L2 loss가 cycle consistency loss이다.
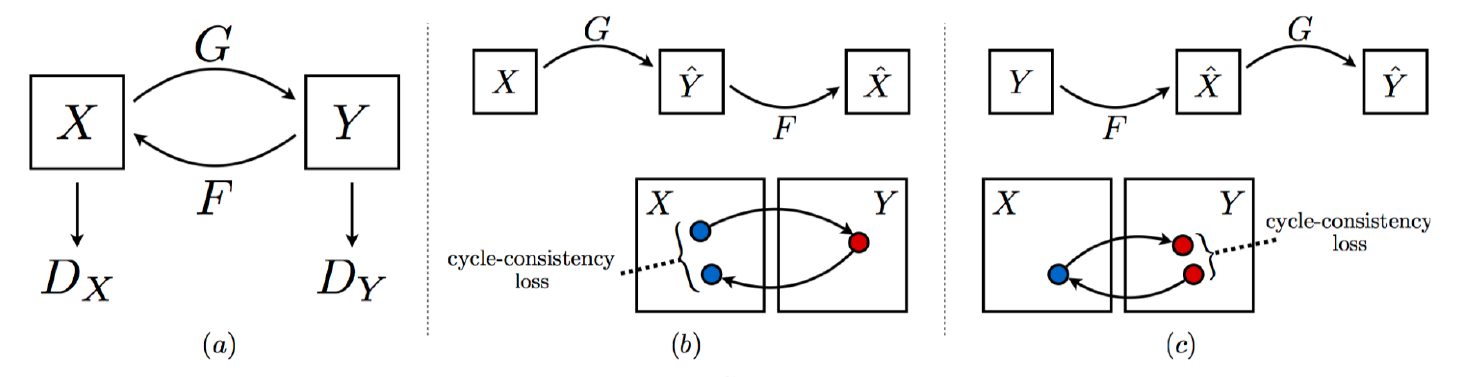
    • 서로 다른 GAN 네트워크를 2개 사용하였기 때문에 cycle-cosistency loss를 줄일 수 있다.
    • GAN이 1개일 때는 우리가 기존에 구하던 loss는 줄어들 수 있지만, cycle-consistency loss의 최소화를 보장하지 못한다.
    • cycle consistency loss는 중요한 concept이니 잘 알아두도록 하자.
• Star-GAN
  • 이미지를 단순히 생성하거나, 이미지의 도메인을 바꾸는게 아니라 이미지 자체를 컨트롤할 수 있는 모델이다.
  • 예를 들어 사람으로 치면 성별을 바꾸거나, 피부 색을 바꾸거나, 눈 모양, 입 모양 등을 바꾸어 이미지에서 드러나는 감정도 바꿀 수 있는 모델이다.
• Progressive-GAN
  • 고차원(고해상도)의 이미지를 생성할 수 있는 모델이다.
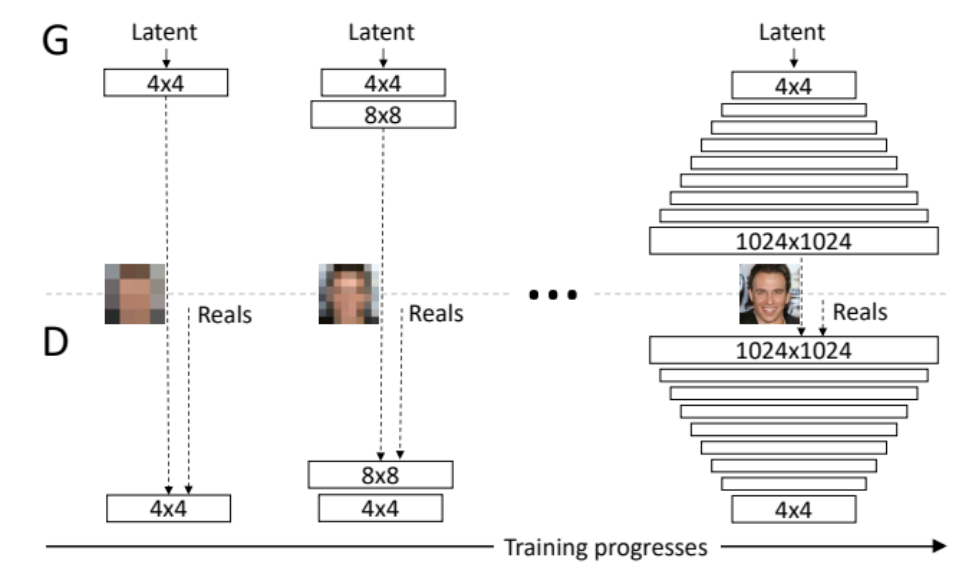
  • 위와 같이 레이어의 크기를 점점 늘려간다는 아이디어에 기반하여 네트워크의 부담을 최대한 줄이면서 고해상도 이미지를 생성할 수 있다.

그 외에도 최근 굉장히 많은 GAN 관련 논문이 세계에서 쏟아지고 있다고 한다. 따라서 앞으로도 GAN에 대해 관심을 가지되, 모두 알려고 하지 말고 중요한 아이디어들을 위주로 잘 캐치해나가야할 필요성이 있다. 또한 VAE와 GAN간의 차이점을 이해하고 상황이 주어졌을 때 VAE와 GAN 중 어떤 것을 활용할지 고를 수 있는 시각을 기르자.

Reference

Pixel Recurrent Neural Network
오토인코더의 모든 것 - 1편~3편
[AutoEncoder의 모든것] Variational AutoEncoder란 무엇인가
VARIATIONAL-AUTOENCODER와 ELBO(EVIDENCE LOWER BOUND)
1시간만에 GAN(Generative Adversarial Network) 완전 정복하기
Generative Adversarial Network

---