개요
오늘은 pandas의 첫 파트와 신경망 및 역전파에 대해 다루었다. 오늘 신경망 파트에서 배운 부분들은 사실 현대에 와서는 실제로 어느정도까지 쓰이는지 잘 모르겠다. 하지만 최근의 알고리즘도 모두 옛날의 것에 근간을 삼을 것이기 때문에 정확히 이해하고 넘어가는 것이 중요할듯하다.
오늘 배운 내용은 아래와 같다.
pandas (Part 1)
pandas는 스프레트시트 처리 기능을 제공하는 Python 라이브러리이다.
Series
- pandas의 테이블은 DataTable 전체를 포함하는 DataFrame object와 그 DataFrame 중 하나의 Column에 해당하는 Series object로 구성되어있다.
따라서 Series 객체는 하나의 column vector라고 할 수 있다. Series 객체는numpy.ndarray의 subclass이다. -
valuesattribute로 값 리스트를,indexattribute로 Index 리스트를 받아올 수 있다.
DataFrame
- DataFrame에는 당연히 서로 다른 데이터타입의 Series가 들어갈 수 있다.
-
index함수를 이용하여 index 행번호를 바꿀 수 있다.reset_index함수로 0부터 시작하는 index로 재설정할 수 있다.inplace옵션을 주어야 원본 객체도 바뀐다. -
loc(index location),iloc(index position) 함수로 데이터를 행/열 단위로 가져올 수 있다. 슬라이싱도 가능하고, 인덱스 지정도 가능하다.loc는 row/column 이름으로,iloc는 인덱스 넘버로 가져온다는 차이점이 있다. -
del,drop으로 원하는 column을 삭제할 수 있다.del은 메모리를 지우기 때문에inplace가 필요 없고 원본에 바로 적용된다.drop은 지운 데이터프레임을 반환하고 원본은 훼손되지 않는다.inplace옵션을True로 주면 원본도 바뀐다.
selection & drop
- 원하는 column이나 row를 아래와 같이 선택할 수 있다.
#selection.py ... ### 1) df["account"].head(3) # account 열만 가져와서 상위 3개행 반환 ### 2) df[["account", "street", "state"]].head() # account, street, state 열들을 가져와서 상위 5개행 반환 ### 3) df[:3] # 상위 3개행 반환 (모든열) # column 이름 없이 사용하는 index number는 row 기준이다. ### 4) df["name"][:3] # account 열의 상위 3개행 반환 # 함께 사용하면 앞은 column, 뒤는 row를 의미한다. ### 5) account_series = df["account"] # Series 반환 account_data_frame = df[["account"]] # DataFrame 반환 ### 6) account_series[:3] # Series의 상위 3개행 반환 account_series[[0, 1, 2]] # 1개 이상의 index 지정 account_serires[list(range(0, 15, 2))] # 당연히 가능 account_serires[account_serires < 250000] # boolean index 사용도 가능하다. ### 7) df["name":"street"][:2] df[["name", "street"]][:2]- pandas에서 row 선택, column 선택 방법은 조금 일관성이 떨어진다
 따라서 잘 알아두도록 하자.
따라서 잘 알아두도록 하자. - 1, 2번을 보면 column 이름으로 테이블을 가져온다. 5번과 같이보면 좋은데 parameter로 list를 주면 DataFrame을, string만 주면 Series를 반환한다.
head()함수가 default로 상위 5개의 행을, parameter를 넣어주면 그 개수만큼 상위 행을 가져온다는 점도 기억해두자. - 3번과 같이 string이 아닌 integer를 주면 column이 아닌 row를 가져온다.
- 4번처럼 인자를 2개 주면 앞에 column명, 뒤에 row index를 쓴다. 3번, 7번처럼 row, column 모두 split을 사용할 수 있다.
- 6번처럼
list(range())혹은 boolean index를 사용해도 당연히 원하는 행을 가져올 수 있다. 둘 모두 리스트를 반환하기 때문이다.
- pandas에서 row 선택, column 선택 방법은 조금 일관성이 떨어진다
- 대신
loc,iloc함수를 사용할 수도 있다.#loc_iloc.py ... df.loc[[219, 323], ["name", "street"]] # 열 index번호 219, 323에서 name, street column만 가져온다. df.iloc[:10, :3] # 처음 10개 행에 대하여 앞 3개 column 정보만 가져온다. -
drop함수로 행 삭제를 할 수 있다.axis옵션을 주면 열삭제도 가능하다.#drop.py ... df.drop(1) # 1번 행(즉, 2번째 행)을 삭제한 DataFrame 반환 # df.drop(1, inplace=True) # inplace 옵션을 주면 원본이 바뀐다. (이 경우 반환객체 없음) df.drop([0, 1, 2, 3]) # 0~3번행 삭제 df.drop("city", axis=1) # axis=1 옵션을 주면 열을 삭제할 수 있다. ('city'열 삭제) df.drop(["city", "state"], axis=1) # 다중열 삭제
dataframe operations
- 두 Series 간의 사칙연산의 경우 index 기준으로 연산을 수행하며, 겹치는 index가 없으면 NaN 값으로 반환한다.
- 두 DataFrame 간의 연산은 column과 index를 모두 고려한다. 둘 모두 일치하는 것만 정상적으로 연산이 수행되며 마찬가지로 겹치지 않으면 해당 부분은 NaN이 반환된다.
-
fill_value옵션을 주면 계산이 불가능한 부분에는 0이 입력된다. - DataFrame과 Series 간의 연산은 옵션으로 준
axis값에 따라 broadcasting이 발생한다.#dataframe_operation.py df1 = DataFrame(np.arange(9).reshape(3, 3), columns=list("abc")) # a b c # 0 0 1 2 # 1 3 4 5 # 2 6 7 8 df2 = DataFrame(np.arange(16).reshape(4, 4), columns=list("abcd")) # a b c d # 0 0 1 2 3 # 1 4 5 6 7 # 2 8 9 10 11 # 3 12 13 14 15 df1.add(df2, fill_value=0) # a b c d # 0 0.0 2.0 4.0 3.0 # 1 7.0 9.0 11.0 7.0 # 2 14.0 16.0 18.0 11.0 # 3 12.0 13.0 14.0 15.0 s = Series(np.arange(10, 14), index=list("abcd")) # a 10 # b 11 # c 12 # d 13 df2 + s # a b c d # 0 10 12 14 16 # 1 14 16 18 20 # 2 18 20 22 24 # 3 22 24 26 28 s2 = Series(np.arange(10, 14)) # 0 10 # 1 11 # 2 12 # 3 13 df2 + s2 # a b c d 0 1 2 3 # 0 NaN NaN NaN NaN NaN NaN NaN NaN # 1 NaN NaN NaN NaN NaN NaN NaN NaN # 2 NaN NaN NaN NaN NaN NaN NaN NaN # 3 NaN NaN NaN NaN NaN NaN NaN NaN df2.add(s2, axis=0) # a b c d # 0 10 11 12 13 # 1 15 16 17 18 # 2 20 21 22 23 # 3 25 26 27 28
lambda, map, apply
-
map함수로 Python의 리스트에서처럼 매핑이 가능하다. - 마찬가지로 매핑시에 없는 값은 NaN으로 표시된다.
map함수의 데이터 변환 기능만replace함수로 사용할 수 있다.#map.py # f = lambda x: x**2 def f(x): return x + 5 s1 = pd.Series(np.arange(6)) s1.map(f) # 0 5 # 1 6 # 2 7 # 3 8 # 4 9 # 5 10 z = {1: "A", 2: "B", 3: "C"} s1.map(z) # 0 NaN # 1 A # 2 B # 3 C # 4 NaN # 5 NaN s2 = pd.Series(np.arange(10, 30)) s1.map(s2) # 0 10 # 1 11 # 2 12 # 3 13 # 4 14 # 5 15#replace.py ... def change_sex(x): return 0 if x == "male" else 1 df.sex.map(change_sex) # 0 1 # 1 0 # 2 1 # 3 0 # 4 0 # 5 1 # .... df["sex_code"] = df.sex.map({"male": 0, "female": 1}) df.sex.replace({"male": 0, "female": 1}) df.sex.replace(["male", "female"], [0, 1], inplace=True) # 모두 비슷한 역할을 수행한다. # 다만, map을 이용하는 첫 줄은 sex_code라는 새로운 열을 생성한다. # replace의 경우 열 생성 없이 해당 열에서 바로 작업을 수행한다. -
apply함수는map과 비슷한데 지정된 column(series)에서만 매핑을 수행한다.#apply.py f = lambda x: np.mean(x) df_info.apply(f) # df_info.apply(np.mean) # df_info.mean() # 각 열들의 평균을 계산해준다. # 예를 들어.. # earn 32446.292622 # height 66.592640 # age 45.328499 # 시리즈 값 반환도 가능하다. def f(x): return Series( [x.min(), x.max(), x.mean(), sum(x.isnull())], index=["min", "max", "mean", "null"], ) df_info.apply(f) # earn height age # min -98.580489 57.34000 22.000000 # max 317949.127955 77.21000 95.000000 # mean 32446.292622 66.59264 45.328499 # null 0.000000 0.00000 0.000000 - 그 외
applymap함수로 series 단위가 아닌 element 단위로 함수를 적용할 수도 있다.
pandas built-in functions
-
describe함수로 numeric type 데이터의 요약정보를 볼 수 있다. numeric type이 아니면 NaN이 표시된다. -
unique함수로 series data의 유일한 값 list를 반환한다.enumerate함수와 같이 사용하면 dict type으로 index를 붙일 수 있을 것이다. -
isnull함수로 각 셀의 값이 null인지 아닌지 확인할 수 있다. boolean table이 반환된다. -
sort_values함수로 해당 column 값을 기준으로 데이터를 sorting할 수 있다. - 그 외
sum,corr,cov,corrwith등의 함수로 통계적인 값이나 단순 연산의 결과를 테이블로 바로 반환받을 수 있다.
신경망과 역전파
우선 신경망에 대해 다루기 전에 선형모델과 비선형모델의 차이점부터 짚고 넘어가자.
선형모델과 비선형모델
일반적으로 $y$와 $x$의 관계가 일차식이면 모두 선형모델이라고 착각하기 쉬운데 이것은 크나큰 오해이다.
우리가 관심을 가져야할 것은 $x$로 나타낸 식이 일차식이냐 아니냐가 아니라 우리가 추정할 대상인 파라미터가 어떻게 생겼느냐이다.
예를 들어, 만약 어떤 파라미터 뒤의 다항식이 $x^{2}$이더라도 $x^{2}$을 $x_{r}$로 치환해버리면 그만이다.
선형모델은 문자항이 아닌 파라미터 부분이 선형식으로 표현되는 모델이다.
어떤 식을 선형모델로 표현할 수 없는 경우는 파라미터의 결합 형태가 복잡하여 선형 모델로 표현할 수 없을 때 발생한다.
딥러닝에서는 파라미터의 결합형태가 매우 다양하기 때문에 선형 모델만으로 표현할 수 없는 모델은 비선형모델을 사용한다.
에서 이 내용에 대해 자세히 설명하고 있다.
신경망의 수식 표현
보통 신경망이라고 하면 아래와 같은 형태를 떠올릴 것이다.
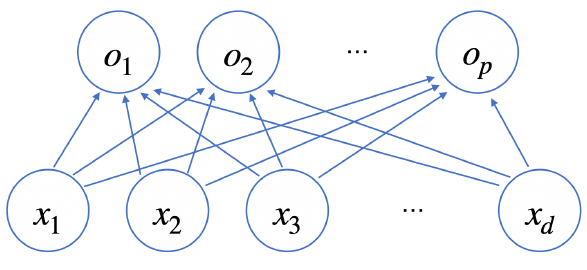
각 $x_{i} (1 \leq i \leq d)$에서 $p$개의 $o_{j} (1 \leq j \leq p)$ 노드로 화살표를 쏘아주는데, 각 화살표에는 고유의 가중치 값 $w_{ji}$가 존재한다.
즉, $x_{i}$ 노드에 $w_{ji}$가 곱해진 값이 $o_{j}$에 더해지는 것이다. 따라서 아래 식이 성립한다.
$n$개의 입력에 대한 출력 값을 동시에 얻기 위해 이를 행렬로 써주면 아래와 같다. 출력 벡터의 차원이 $d$에서 $p$로 바뀌게 된다.
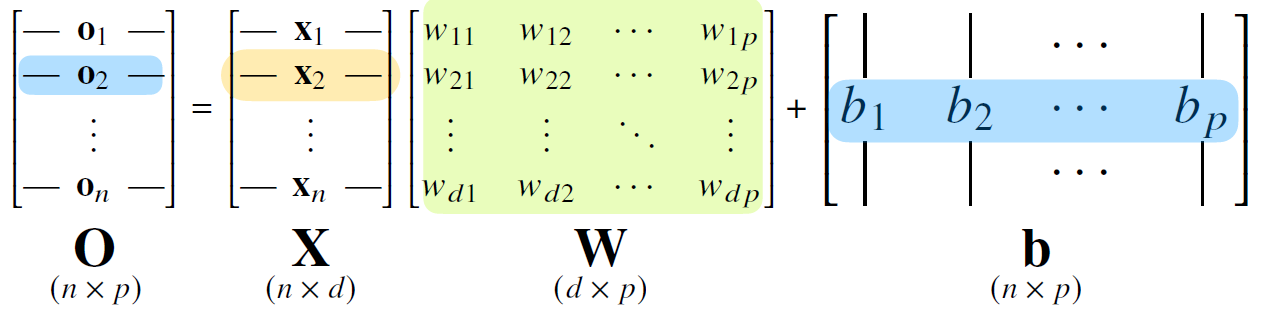
위 신경망 이미지를 기준으로 각 $\text{x}_{i}$는 $x_{1}, x_{2}, \cdots, x_{d}$로 이루어져있으며, 각 $\text{o}_{j}$는 $o_{1}, o_{2}, \cdots, o_{p}$로 이루어져있다는 점에 유의한다. 우리는 하나의 입출력 데이터가 아닌 여러 입출력 데이터를 다룰 것이며 그렇기 때문에 행렬을 통해 연산을 표현하는 것이다.
$\text{b}$는 절편값을 나타내는 행렬으로, 모든 행이 같은 값을 가진다.
소프트맥스 함수
소프트맥스(softmax) 함수는 각 input을 0과 1사이의 값으로 정규화해주며 정규화된 값의 합은 1이 된다.
즉, 이 함수는 모델의 출력을 확률로 해석할 수 있게 변환해준다.
$\text{softmax}(\text{o})=\left(\frac{\text{exp}(o_{1})}{\sum_{k=1}^{p} \text{exp}(o_{k})}, \cdots ,\frac{\text{exp}(o_{p})}{\sum_{k=1}^{p} \text{exp}(o_{k})}\right) = \left(p_{1}, \cdots, p_{k}\right) = \hat{y}$
$\text{exp}(x)$ 함수는 exponential 함수를 의미하며, $e^{x}$와 같은 의미이다.
softmax 함수의 parameter로는 당연히 이전에 구한 $\text{o}$벡터, 즉 $\text{Wx} + \text{b}$가 들어갈 것이다.
분류 문제를 풀 때 선형모델과 소프트맥스 함수를 결합하여 예측한다.
학습시킬 때는 softmax 함수를 사용하나, 실제 추론을 할 때는 one-hot 벡터로 최댓값을 가진 주소만 1로 출력하는 연산을 사용한다는 점에 유의한다.
아래는 소프트맥스 함수의 실제 구현이다. 특이한 점은 분자에서 최댓값을 뺀 값에 지수함수를 취한다는 점이다.
#softmax.py
import numpy as np
def softmax(vec):
# overflow를 방지하기 위해 max값을 빼준다.
denumerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True))
numerator = np.sum(denumerator, axis=-1, keepdims=True)
val = denumerator / numerator
return val
vec = np.array([[1, 2, 0], [-1, 0, 1], [-10, 0, 10]])
softmax(vec)
# array([[2.44728471e-01, 6.65240956e-01, 9.00305732e-02],
# [9.00305732e-02, 2.44728471e-01, 6.65240956e-01],
# [2.06106005e-09, 4.53978686e-05, 9.99954600e-01]])
이는 지수함수의 특성에 따라 지수가 커질수록 $y$ 값이 기하급수적으로 증가하기 때문에 컴퓨터의 overflow을 방지하기 위한 조치라고 할 수 있다. 이런 트릭을 사용하면 오버플로우를 방지하는 동시에, 원하는 값을 얻을 수 있다.
앞서 언급했듯이 실제 추론에서는 softmax 함수를 사용하지 않고 바로 one hot encoding을 하면 원하는 값을 얻을 수 있다.
#one_hot.py
...
def one_hot(val, dim):
# 단위 행렬에서 i번째 행은 i번째 열만 값이 1이다.
return [np.eye(dim)[_] for _ in val]
def one_hot_encoding(vec):
vec_dim = vec.shape[1]
vec_argmax = np.argmax(vec, axis=-1)
return one_hot(vec_argmax, vec_dim)
print(one_hot_encoding(vec))
# [array([0., 1., 0.]), array([0., 0., 1.]), array([0., 0., 1.])]
활성 함수
활성 함수(activation function)는 실수 위에 정의된 비선형함수로, 신경망에서 입력받은 데이터를 다음층으로 출력할지를 결정한다.
활성함수를 쓰지 않으면 딥러닝은 선형모형과 차이가 없다. 뉴런은 임계치를 넘을때만 값을 출력해야하며, 그 과정에서 활성함수를 사용한다.
과거에는 sigmoid함수와 tanh함수를 많이 사용하였으나, 최근에는 보통 ReLU 함수를 많이 사용한다.
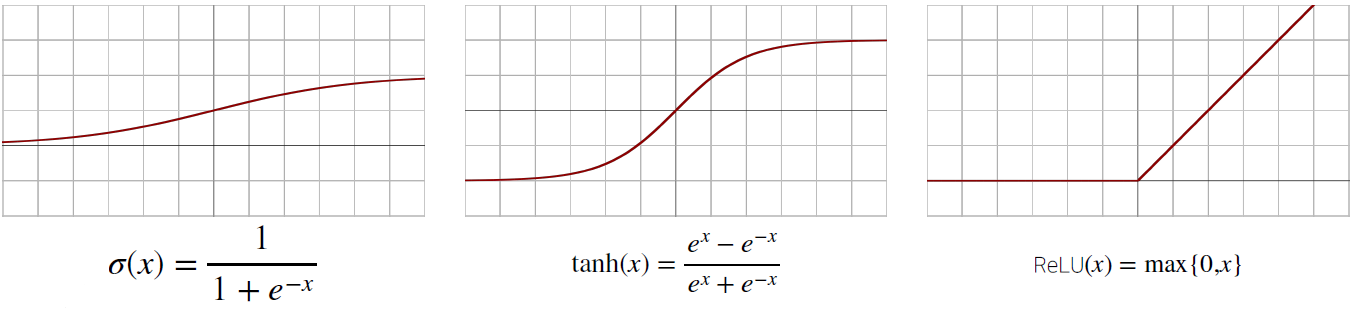
각 함수의 장단점과 개선방향을 서 확인하고 넘어가자.
간단하게 말하면, sigmoid 함수와 tanh 함수는 gradient vanishing($x$의 절댓값이 어느정도 커지면 미분값이 소실(0)되는 문제)으로 인해 잘 사용하지 않는다.
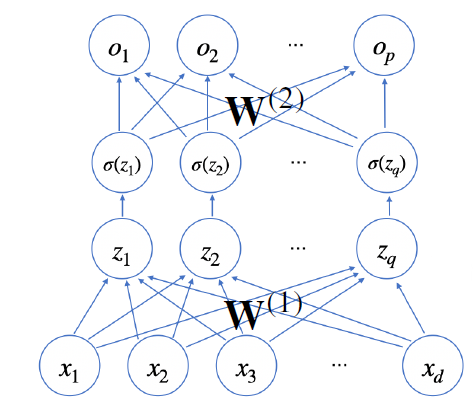
위와 같이 활성 함수는 어떤 한 층을 지나고 나온 출력값에 적용한다. 이후 해당 출력은 다음 층의 입력으로 들어가게 된다.
따라서 신경망은 선형모델과 활성 함수를 합성한 함수라고 볼 수 있다.
활성 함수를 통과한 벡터를 $\text{H}$로 표기하며 잠재벡터라고 부른다.
$\text{H} = (\sigma(z_{1}), \cdots, \sigma(z_{n}))$
$\text O = \text H \text W ^{(2)} + \text b ^{(2)}$
이 때 $\text W ^ {(t)}$와 $\text b ^{(t)}$는 $t$번째 신경망의 가중치와 절편이다.
위 신경망을 $(\text W ^ {(2)}, \text W ^ {(1)})$를 parameter로 하는 2층(2-layers) 신경망이라고 부른다.
다중(multi-layer) 퍼셉트론(MLP)은 신경망이 여러층 합성된 함수이다.
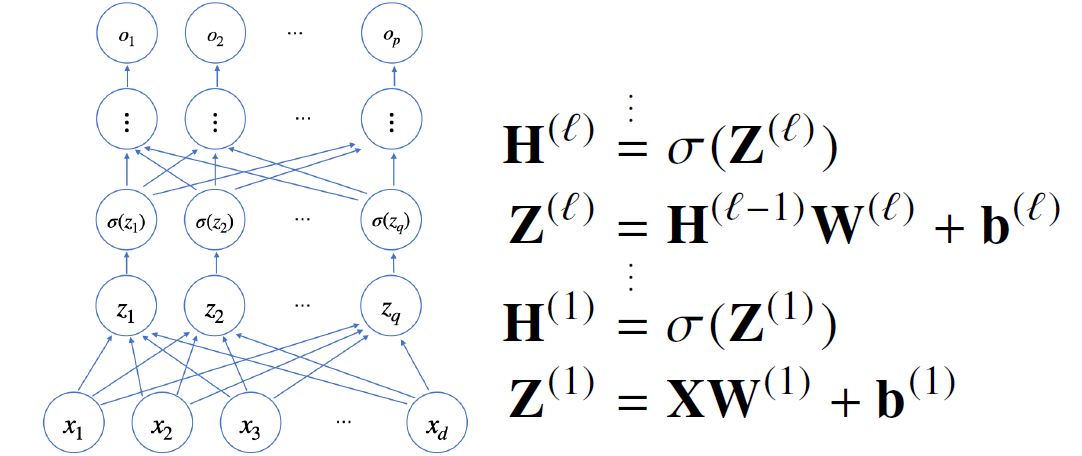
이제 위 수식을 이해할 수 있다. MLP가 총 $L$개의 가중치 행렬과 절편 행렬으로 이루어져있다고 하자.
$\ell-1$번째 잠재함수 $\text{H} ^{(\ell - 1)}$는 다음 가중치 행렬 $\text{W} ^{(\ell)}$과 곱해진 후 가중치 $\text b ^{(\ell)}$와 더해져 출력값 $Z ^{(\ell)}$이 된다. 이후 다시 활성 함수 $\sigma(x)$를 거치고 $\text H^{(\ell)}$이 된다.
층을 왜 여러개 쌓을까?
- 이론적으로는 2층 신경망으로도 임의의 연속함수를 근사할 수 있다. (universal approximation theorem)
- 그러나 실제 적용에서는 2층만으로는 무리가 있다. 층이 깊을수록 목적함수로 근사하는데 있어 필요한 노드(뉴런)의 개수가 빠르게 줄어들기 때문에 층이 깊어질수록 적은 parameter로 복잡한 함수를 표현할 수 있다. 즉, 층이 얇으면 신경망의 너비가 늘어나게 된다.
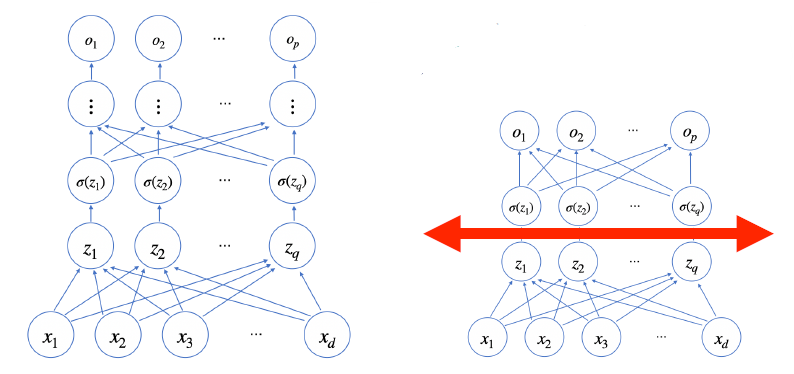
층이 얇으면 필요한 뉴런의 개수가 늘어나 넓은 신경망이 되어야 한다.
- 하지만 층이 깊다고 정확도가 꼭 좋은 것은 아니다. 최적화가 어려워지며 특히 활성 함수를 여러번 통과하면 유의미한 값이 사라질 가능성도 있다.
지금까지의 살펴본 것은 신경망의 순전파(forward propagation)이었다.
역전파 알고리즘
순전파(forward propagation)로는 추론만 가능하고 학습이 불가능하다. 우리는 경사하강법에서 했던 것처럼 매 학습마다 가중치 값을 업데이트해주면서 결론적으로 오차가 최소가 되는 가중치를 찾아야한다.
이를 위해 역전파(backpropagation) 알고리즘을 이용한다. 역전파 알고리즘을 통해 각 층에 사용된 parameter(가중치)들을 학습시킬 수 있다.

우리의 목표는 결국 위와 같은 신경망에서 오차의 각 가중치에 대한 미분값 즉 $\dfrac{\partial E _{\text{total}}}{\partial \text W _{ij} ^{(\ell)}}$을 구하는 것이다.
이 때, $\text W _{ij} ^{(\ell)}$는 $\ell$번째 층의 $i$번째 입력값과 $j$번째 출력값 사이의 가중치이다.
이제 이 식은 다음과 같이 나타낼 수 있다.
$i$는 $x_k$의 인덱스를, $j$는 $z_k$의 인덱스를, $l$은 $o_k$의 인덱스를 의미한다.
$\sum\limits _{l}$은 출력값 $o_{l}$ 전체에 대한 편미분이 필요하기 때문에 붙게 된다.
그래서 사실 서로 다른 가중치에 대한 미분값을 구할 때 같은 출력값에 대한 미분값을 여러번 사용하게 된다. 따라서 이런 값들은 메모리에 저장해서 여러 번 사용하는 것이 좋고, 실제로도 그렇게 구현한다.
여타 몇몇 블로그에서는 이렇게 기억해야 할 미분값을 $\delta _{j} ^{(\ell)}$로 표현하고 있는 것 같다.
이제 시그마 뒤에 붙은 식들의 의미를 하나하나 이해해보자.
먼저 $E _{\text{total}}$은 목표값 $\text{target} _{l}$과 실제 출력 $o_{l}$에 대하여
$\dfrac{\partial E _{\text{total}}}{\partial o_{l}} = - \left( target _{l} - o_{l} \right)$
이다.
$h_{j}$는 활성 함수를 통과한 출력값 즉 $h_{j} = \sigma(z_{j})$이다.
$\dfrac{\partial o_{l}}{\partial h_{j}} = \text W ^{(\ell + 1)} _{jl}$
이다.
이어서,
$\dfrac{\partial h_{j}}{\partial z_{j}} = \sigma'(z_{j}) = \sigma(z_{j}) \left( 1 - \sigma(z_{j}) \right)$
활성 함수 $\sigma(x)$를 sigmoid 함수라고 가정했을 때 미분은 위와 같다.
마지막으로,
$\dfrac{\partial z_{j}}{\partial \text W _{ij} ^{(\ell)}} = x_{i}$
정리하면 다음과 같다.
이제 이것을 이용하여 앞서 배운 경사하강법에서처럼 가중치를 업데이트하면 된다.
$$ \text W ^{(\ell)} := \text W ^{(\ell)} + \sum\limits _{l} \left( target _{l} - o_{l} \right) \text W ^{(\ell + 1)} _{jl} \sigma'(z_{j}) x_{i} $$
역전파 알고리즘은 ‘역전된’ 순서로 값을 업데이트하기 때문에 뒷단계의 가중치 값을 앞단계 업데이트에 이용한다.
이렇게 역전파 알고리즘까지 알아보았는데, 앞서 말했듯이 실제 계산시에는 동일 층에서의 가중치 업데이트시에 같은 값을 여러번 사용하므로 실제로는 컴퓨터 메모리에서 해당 값을 기억하고 있는 것이 좋다.
식이 좀 복잡하긴한데 어차피 계산은 컴퓨터가 하기 때문에 ![]() 원리를 기억하는데에 집중하도록 하자.
원리를 기억하는데에 집중하도록 하자.