개요
미분의 개념에 대한 간단한 복습 이후 경사하강법을 통해 선형회귀 계수를 구하는 과정을 살펴보았다. 그리고 실제 적용에서 더 많이 쓰이는 확률적 경사하강법(SGD)에 대해 다루었다.
오늘 배운 내용은 아래와 같다.
경사하강법
미분에 대한 개념을 간단히 복습하고 경사하강법에 대해 다루었다.
미분(differentitaion)
- 미분의 경우 Python의
sympy.diff로 계산할 수 있다.sympy는 symbolic mathematics를 위한 python 라이브러리의 약자이다.#diff.py import sympy as sym from sympy.abc import x sym.diff(sym.poly(x**2 + 2*x + 3), x) # Poly(2𝑥+2,𝑥,𝑑𝑜𝑚𝑎𝑖𝑛=ℤ) - 한 점에서 어느 방향으로 점을 움직여야 함수값이 증가 혹은 감소하는지 알기 위해 미분을 사용한다.
- 물론 어느 정도까지는 직접 눈으로 보고 알 수 있지만, 3차원부터는 그래프를 그리기도 힘들뿐더러 그보다 더 고차원이 되면 눈으로 보고 판단하기 힘들다. 그래서 미분을 사용한다.
- 당연한 이야기지만, 미분값이 음수이면 $x$가 증가할 때 $y$값 감소, 미분값이 양수이면 $x$가 증가할 때 $y$값은 증가한다.
경사하강법(일변수 함수)
미분값을 더하면 경사상승법이라고 하며, 함수의 극댓값을 구할 때 사용한다.
반대로 미분값을 빼면 경사하강법이라고 하며, 함수의 극솟값을 구할 때 사용한다.
각각의 경우를 그래프로 직접 그려보면 왜 각각에서 미분값을 더하고 빼는지 쉽게 알 수 있다.
- 경사하강법 알고리즘은 아래 pseudo code로 동작한다.
#gradient_descent_pseudo_code.py # Input: gradient, init, lr, eps, Output: var # gradient: 도함수 # init: 초기값, lr(learning rate): 학습률 # eps(epsilon): 알고리즘 종료 조건 (0에 가까운 값) var = init grad = gradient(var) while abs(grad) > eps: var = var - lr * grad grad = gradient(var) - 엡실론을 쓰는 이유는 컴퓨터의 연산 결과가 정확히 0에 도달하는 것은 거의 불가능하기 때문이다.
- 일변수 함수에 대하여 아래와 같이 경사하강법을 간단하게 적용할 수 있다.
#gradient_descent.py import numpy as np import sympy as sym from sympy.abc import x def func(val): fun = sym.poly(x**2 + 2*x + 3) return fun.subs(x, val), fun def func_gradient(fun, val): _, function = fun(val) diff = sym.diff(function, x) return diff.subs(x, val), diff def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5): cnt = 0 val = init_point diff, _ = func_gradient(fun, init_point) while np.abs(diff) > epsilon: val = val - lr_rate * diff diff, _ = func_gradient(fun, val) cnt += 1 print(f"함수: {fun(val)[1]}, cnt: {cnt}") print(f"최소점: ({val}, {func(val)[0]})") gradient_descent(fun=func, init_point=np.random.uniform(-2, 2)) # 함수: Poly(x**2 + 2*x + 3, x, domain='ZZ'), cnt: 535 # 최소점: (-1.00000496557233, 2.00000000002466)
경사하강법(다변수 함수)
- 다변수 함수에 대하여서도 편미분을 활용하여 경사하강법을 적용할 수 있다.
-
각 변수별로 편미분을 계산한 그래디언트 벡터(gradient vector)를 경사하강법에 이용할 수 있다.
$\nabla f = (\partial_{x1}f, \partial_{x2}f, ... , \partial_{x_{d}}f)$ 좌변의 뒤집어진 delta 기호를 nabla라고 부른다.
- 각 점 $(x, y, z)$ 공간에서 $f(x, y)$ 표면을 따라 $-\nabla f$ 벡터를 그리면 아래와 같이 극솟점으로 모이는 그래프가 그려진다.
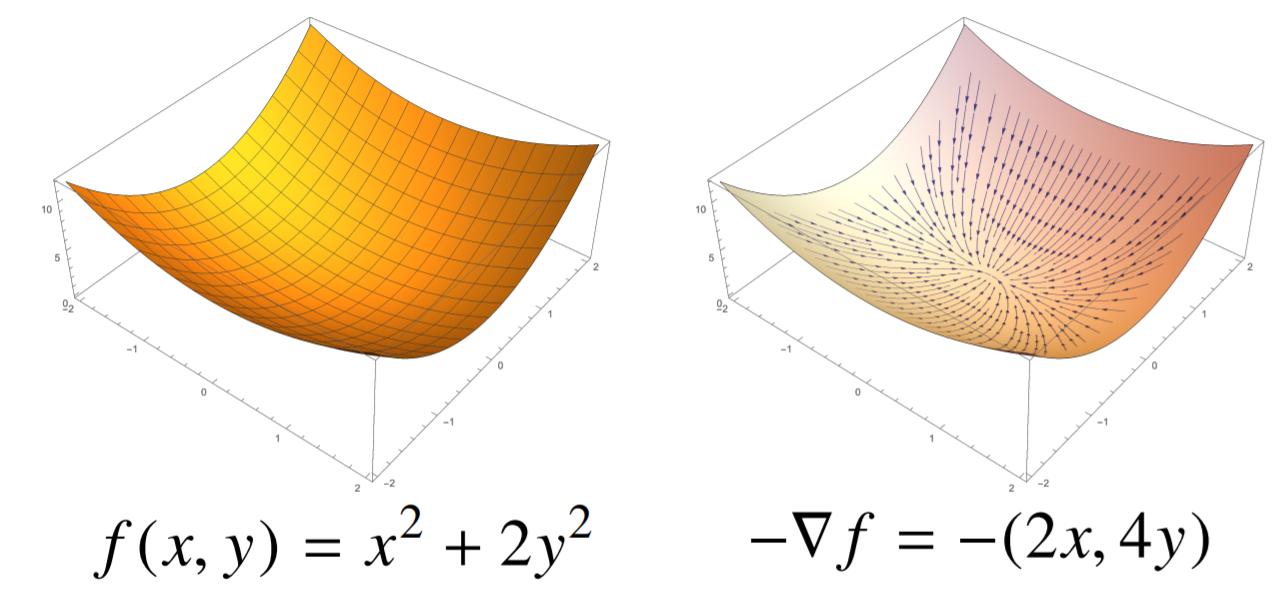
- 그래디언트 벡터 $\nabla f(x, y)$는 각 점 $(x, y)$에서 가장 빨리 증가하는 방향으로 흐르게 된다.
- 따라서 해당 그래디언트 벡터에 음의 부호를 취한 값을 이용하여 경사하강법에 사용한다.
- 다변수 함수에서의 경사하강법 알고리즘은 아래 pseudo code로 동작한다.
#multivariate_gradient_descent_pseudo_code.py # Input: gradient, init, lr, eps, Output: var # gradient: gradient vector # init: 초기값, lr(learning rate): 학습률 # eps(epsilon): 알고리즘 종료 조건 var = init grad = gradient(var) while norm(grad) > eps: # 조건문의 grad에 절댓값 대신 norm이 붙었다는 것이 차이점 var = var - lr * grad grad = gradient(var) - 실제 구현도 일변수 함수와 거의 같다.
#multivariate_gradient_descent.py import numpy as np import sympy as sym from sympy.abc import x, y def eval_(fun, val): val_x, val_y = val fun_eval = fun.subs(x, val_x).subs(y, val_y) return fun_eval def func_multi(val): x_, y_ = val func = sym.poly(x**2 + 2*y**2) return eval_(func, [x_, y_]), func def func_gradient(fun, val): x_, y_ = val _, function = fun(val) diff_x = sym.diff(function, x) diff_y = sym.diff(function, y) grad_vec = np.array([eval_(diff_x, [x_, y_]), eval_(diff_y, [x_, y_])], dtype=float) # 이전과 달리 벡터를 계산하고, 반환한다. return grad_vec, [diff_x, diff_y] def gradient_descent(fun, init_point, lr_rate=1e-2, epsilon=1e-5): cnt = 0 val = init_point # 변수 2개로 이루어진 리스트 diff, _ = func_gradient(fun, val) while np.linalg.norm(diff) > epsilon: val = val - lr_rate * diff diff, _ = func_gradient(fun, val) cnt += 1 print(f"함수: {fun(val)[1]}, cnt: {cnt}") print(f"최소점: ({val}, {func(val)[0]})") pt = [np.random.uniform(-2, 2), np.random.uniform(-2, 2)] gradient_descent(fun=func_multi, init_point=pt) # 함수: Poly(x**2 + 2*y**2, x, y, domain='ZZ'), cnt: 609 # 최소점: ([-4.94..e-06 2.81..e-11], # Poly(x**2 + 2*x + 3, x, domain='ZZ'))
일괄 경사하강법을 이용한 선형 회귀
Day 6에서 선형회귀계수를 찾을 때 무어-펜로즈 유사역행렬을 활용하였다.
무어-펜로즈 역행렬은 시간복잡도가 $O(n^{3})$으로 높다는 점, 선형 모델에만 적용할 수 있다는 점 등의 단점이 있다.
즉, normal equation으로 푸는 방법은 시간복잡도가 높다.
경사하강법은 비선형 모델에도 적용할 수 있으며 보다 일반적인 방법으로 활용 가능하다.
- 선형회귀의 목적식은 $\Vert \text{y} - \text{X} \beta \Vert _{2}$이다.
- 이를 최소화하는 $\beta$를 찾아야하므로 아래와 같은 그래디언트 벡터를 구해야한다.
- 간단하게 보기 위해 그래디언트 벡터의 임의의 $k$번째 성분만 뽑아 편미분하면 아래와 같다.
$\partial _{\beta _{k}} \Vert \text{y}-\text{X}\beta \Vert _{2}= -\dfrac{\text{X}^{\text{T}}_{\cdot k} \left(\text{y} - \text{X} \beta \right)}{n \Vert \text{y} - \text{X} \beta \Vert _{2}}$
- 이제 이 결과식을 그래디언트 벡터의 모든 entry에 적용하면 된다. 목적식을 최소화하는 경사하강법 알고리즘을 식으로 표현하면 다음과 같다.
$\beta ^{(t+1)} \leftarrow \beta ^{(t)} - \lambda \nabla _{\beta} \Vert \text{y} - \text{X} \beta ^{(t)} \Vert$
- 원래 식에 음의 부호가 붙어있었으므로 두 식을 합쳐서 정리한 식에서는 편미분 값을 빼려고 하면 앞이 양의 부호가 된다.
- 사실 $\partial _{\beta} \Vert \text{y}-\text{X}\beta \Vert _{2}$ 대신 $\partial _{\beta} \Vert \text{y}-\text{X}\beta \Vert ^{2} _{2}$을 최소화하면 식이 더욱 간단해진다. 어떤걸 최소화하든 구해야하는 $\beta$값은 같다. 목적식에 제곱을 한 후에 계산하면 결과는 아래와 같다.
$\beta ^{(t+1)} \leftarrow \beta ^{(t)} + \dfrac{2\lambda}{n} \text{X} ^{\text{T}} \left(\text{y} - \text{X} \beta ^{(t)} \right)$
- 아래는 지금까지 구한 그래디언트 벡터를 적용한 pseudo code이다.
실제 구현에서는 성능 및 편의를 위해 상수 $\frac{n}{2}$는 제외하고 계산하는 것 같다. 만약 $\frac{n}{2}$도 식에 포함되면 $n$이 조금만 커져도 $\beta$ 값의 업데이트가 매우 느려질 것이다.#linear_regression_with_gradient_descent.py # Input: X, y, lr, T, Output: beta # lr: 학습률, T: 학습횟수 var = init grad = gradient(var) for t in range(T): # 종료조건을 일정 학습횟수로 변경하였다. error = y - X @ beta # var = var - lr * grad grd = -transpose(X) @ error # grad = gradient(var) beta = beta - lr * grad - 아래는 실제 구현 코드이다.
import numpy as np lr = 1e-2 X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]]) y = np.dot(X, np.array([1, 2])) + 3 # [1, 2, 3]이 정답. x + 2y + 3 beta_gd = [10.1, 15.1, -6.5] # intercept항(상수항) 추가 X_ = np.array([np.append(x, 1) for x in X]) for t in range(5000): error = y - X_ @ beta_gd grad = -X_.T @ error beta_gd = beta_gd - lr * grad print(beta_gd) # [1.00000367 1.99999949 2.99999516] # 학습을 너무 적게 하면 오차가 커진다. # 적당한 learning rat 및 test 횟수를 선택하는것이 중요하다. # 초기값 선택도 중요한 요소가 될 수 있다. - 이론적으로 경사하강법은 미분 가능하고 convex(볼록)한 함수에 대하여 수렴이 보장되어있다.
- 적절한 학습률과 학습횟수를 선택하는 것이 매우 중요하다.
-
선형회귀의 목적식 $\Vert \text{y} - \text{X} \beta \Vert$ 역시 볼록 함수이기 때문에 수렴이 보장된다.
- 그런데 비선형회귀 문제의 경우 목적식이 볼록하지 않을 수 있어 수렴이 보장되지 않는다.
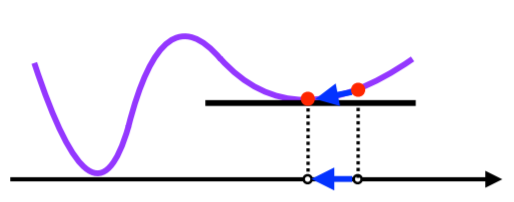
위와 같은 그래프는 볼록함수가 아니다. 딥러닝에서 보게 될 대부분의 목적함수는 convex하지 않다.
- 이러면 $\beta$가 global minimum이 아닌 local minimum에 도달한 경우에도 알고리즘이 멈추는 문제가 생긴다.
확률적 경사하강법(SGD)
우리가 지금까지 배운 경사하강법은 (Full-)Batch Gradient Descent(BGD)로, 전체 데이터셋에 대한 오차를 매 업데이트마다 계산하는 방식이었다.
하지만 해당 방식으로 계산하면 데이터셋이 조금만 많아져도 하드웨어 자원의 측면이나, 시간적 측면으로 여러 문제가 생긴다.
SGD는 Stochastic Gradient Descent의 약자로, 이 기법은 매번 모든 데이터를 사용하는 게 아니라 데이터 한개 또는 일부만을(mini-batch) 활용하여 다음 값을 업데이트한다.
볼록이 아닌(non-convex) 목적식은 SGD를 통해 최적화할 수 있다.
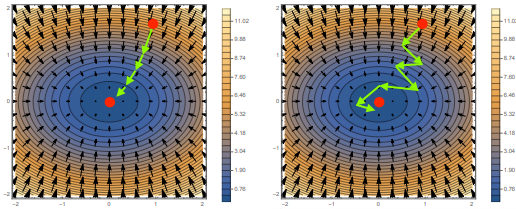
좌측이 BGD, 우측이 SGD이다. SGD를 사용하면 목표값을 향해 좀 더 돌아가는 것처럼 보이지만 실제로는 연산량이 훨씬 적어 더 빠르게 목표지점에 도달할 수 있다.
- 전체 데이터를 활용하지 않고 미니배치$(X_{b}, y_{b})$를 활용하기 때문에 연산량이 $\frac{b}{n}$으로 감소한다G.
- 매 학습마다 전체 데이터 중 확률적으로 mini-batch를 선택하여 error를 구하므로 목적식의 형태가 계속 바뀌게 된다. SGD는 BGD보다 부정확한 결과를 내지만 자원을 덜 쓰기 때문에 연산이 훨씬 간편해진다. 또한 기댓값의 관점에서 SGD역시 BGD와 유사한 결과를 낼 수 있다는 점이 실증적으로 증명되었다.
- 또한 global minimum이 아닌 local minimum을 만나게 될 경우 그 지점에서 탈출할 가능성도 열린다.
- 다만 SGD는 반대로 global minimum에 빠지고 싶어도 빠지지 못한다는 단점이 있다.
- mini-batch를 만들어 사용하는 것은 병렬연산에 유리하며 다양한 목적식에도 활용 가능하다. SGD를 사용하게 된다면 당연히 batch size를 잘 선정해야한다.
그 외
사실 SGD를 변형없이 그대로 사용할 경우 현대에 와서는 성능이 좋은 편이라고 평가받지 못한다.
에서 더 다양한 optimization 기법들을 볼 수 있다.
대부분은 SGD에 기반한 알고리즘들이지만 SGD에 조금 변형을 가함으로써 월등히 성능이 향상되는 것을 확인할 수 있다.