개요
Encoder-Decoder의 구조를 가진 가장 기초적인 모델 Seq2Seq 모델에 대해 알아보고, 이 모델의 단점을 극복하기 위해 함께 사용하는 attention 모듈, Beam search 알고리즘에 대해 알아보도록 한다. 마지막으로 번역 모델의 평가 지표로 사용되는 BLEU에 대해 다루어본다.
아래와 같은 순서로 작성하였다.
Seq2Seq Model
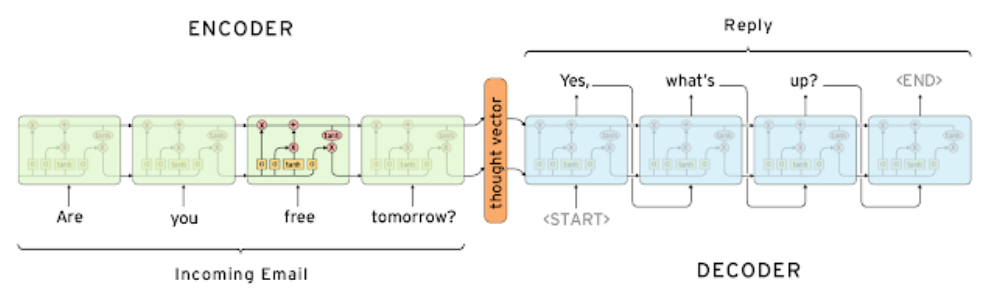
Seq2Seq 모델은 어제 보았던 RNN의 종류 중 many-to-many, 그 중에서도 첫번째 유형에 해당하는 모델이다.
먼저 input을 모두 받아온 후 이를 기반으로 output을 내보내는 형태이다.
위 그림과 같이 Encoder-Decoder 구조로 이루어져있으며, Encoder와 Decoder 모두 LSTM 기반으로 동작한다. (물론 다른 RNN 구조를 사용해도 될 것이다) Encoder에서 input을 받아 hidden state vector를 생성하고, 이를 Decoder의 $h_0$ 벡터로 활용한다. 즉, Decoder에서는 Encoder가 input sequence로부터 생성한 의미있는 hidden state vector를 통해 다시 의미있는 어떤 sequence를 생성할 수 있게 된다. 당연히 Encoder, Decoder는 독립적(parameter를 share하지 않는다)으로 동작한다.
Decoder의 첫 input으로는 ‘<SoS>’ (Start of Sentence) 토큰을 넣어주며 Decoder가 출력하는 ‘<EoS>’ (End of Sentence) 토큰은 문장의 끝을 의미한다. (더이상 generating을 하지 않는다)
가장 기본적인 Seq2Seq 모델은 위와 같은데, 문제는 단순히 Encoder의 마지막 hidden state vector를 Decoder의 $h_0$로 넣어주게 되면 한정된 dimension에 과거의 정보를 모두 우겨넣어야 하는데(bottleneck problem), 이렇게 되면 먼 과거의 정보는 당연히 vanishing이나 degradation이 발생할 수 밖에 없다. 따라서 이를 해결하기 위해 위와 같은 구조에 Attention 구조를 추가적으로 도입함으로써 먼 과거의 정보까지 고려할 수 있는 모델을 만들 수 있게 된다.
Seq2Seq with Attention
Attention 구조는 Encoder의 모든 timestep에서의 hidden state vector를 고려하여 output을 생성할 수 있도록 해준다. 이를 통해 Decoder는 sequence를 생성하는 매 timestep마다 그때그때 필요한 (Encoder의)hidden state vector를 가져다가 쓸 수 있게 된다.
-
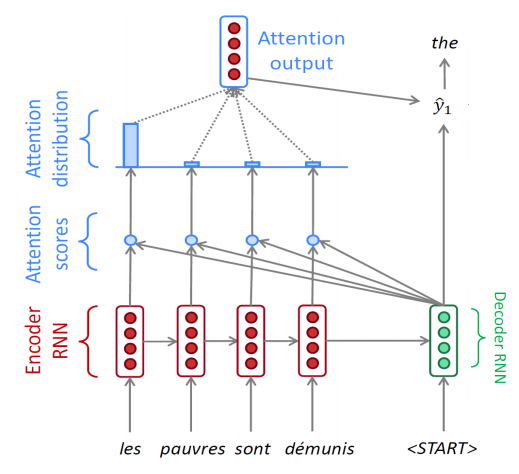
우선 Decoder에 ‘<SoS>’ 토큰과 encoder의 마지막 hidden state vector를 첫 input으로 넣어주는 것까지는 이전과 같다.
-
그 다음, Decoder에서 첫 hidden state vector $h ^{(d)} _1$가 나올텐데, 이 벡터와 이전에 Encoder에서 나온 hidden state vector 4개($h ^{(e)} _1$, $h ^{(e)} _2$, $h ^{(e)} _3$, $h ^{(e)} _4$)와 각각 내적을 취한다. 내적을 하는 것은 유사도를 측정하는 역할을 하는데, 내적 값이 높을 수록 두 벡터가 유사하다(코사인 유사도 측정과 비슷한 맥락)
-
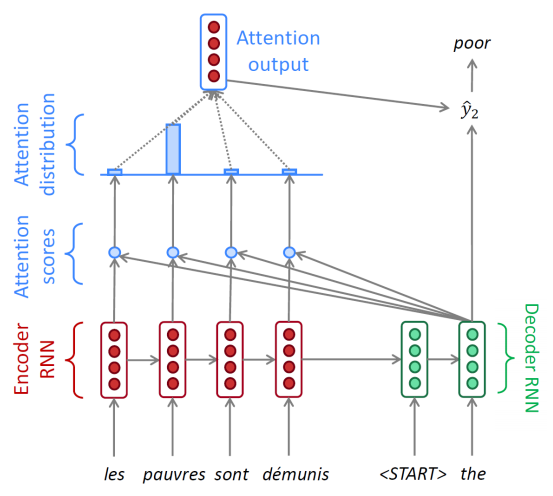
그리고 나온 값에 softmax를 취해 이를 확률으로 변환하고 이를 통해 $h ^{(e)} _1$, $h ^{(e)} _2$, $h ^{(e)} _3$, $h ^{(e)} _4$의 가중평균(weight sum)을 구하면 그것이 attention module의 output이 된다.
-
마지막으로 attention output(=context vector)과 $h ^{(d)} _1$를 concat하여 output layer에 통과시키면 최종적으로 현재 단계의 output $\bar{y} _2$가 나오게 된다.
-
이 과정을 ‘<EoS>’ 토큰이 나올 때까지 반복한다.
예를 들어, 2번에서 나온 내적 값이 [7, 1, -1, -2]였다고 하자. 그리고 이를 softmax로 변환했더니 [0.85, 0.08, 0.04, 0.03]이 나왔다. (실제 계산 결과는 다를 수 있음, 예시임)
그러면 context vector의 값은
$0.85 \cdot h ^{(e)} _1 + 0.08 \cdot h ^{(e)} _2 + 0.04 \cdot h ^{(e)} _3 + 0.03 \cdot h ^{(e)} _4$이 된다.
이를 $h ^{(d)} _1$과 concat하여 output layer에 통과시켜 최종 output을 얻게 된다.
정리하면, Decoder에서 나온 hidden state vector $h ^{(d)} _k$는 output에 직접적으로 관여를 하는 동시에 입력 sequence의 encoding vector 중 어떤 것을 얼마나 가져올지 결정하는데에 관여하게 된다.
Teacher forcing in Seq2Seq
원래 우리는 실제 추론(inference) 단계에서 Decoder에는 이전 단계의 output을 다음의 input으로 넣어주게 된다. 하지만 실제 학습에서는 조금 다를 수 있다. 만약 학습과정에서 전 단계에서 예측을 하나만 잘못해도 그 다음 예측이 모두 뒤엉키게 된다. 이렇게 되면 학습이 매우 느려질 수 있다. 이에 따라 학습을 보다 빠르게 촉진시키고자 Teacher forcing이라는 기법을 도입하게 된다.
Teacher forcing에서는 학습 단계에서 다음의 input으로 이미 알고 있는 ground truth를 넣어준다.
이전의 output이 잘못 나왔더라도 일단은 무시하고 원래 input으로 들어가야할 임베딩 벡터를 넣어주는 것이다.
이렇게 되면 학습이 빨라진다는 장점이 있다. 다만 반대로 학습 자체를 실제와 괴리가 있는 환경에서 하였기 때문에 추론의 성능이 떨어질 우려는 존재한다.
반대로 teacher forcing 없이, 우리가 원래 하던대로(이전 output -> 다음 input) 하면 학습은 느려질 수 있지만 실제 추론 성능이 좀 더 좋은 학습을 할 수 있다는 장점이 있다.
실제 구현에서는 teacher forcing을 초반에만 적용하다가 후반에는 빼는 방법, 혹은 probability를 주어 확률적으로 teacher forcing을 하는 방법 등으로 양 방법의 장점을 모두 취할 수 있도록 활용할 수도 있다.
Different Attention Mechanisms
$h_t$는 decoder의 hidden state, $\bar{h}_s$는 encoder의 hidden state를 의미한다.
attention 모듈의 내적을 하는 부분(scoring)에서 단순한 내적 외에 다른 방법들을 사용해볼 수도 있다.
우선 dot attention은 기존에 썼던 방법이고, general attention은 $h_t$, $\bar{h}_s$와 같은 row/column 길이를 가진 정사각 행렬을 중간에 추가하여 단순한 내적을 보다 일반화된 dot product로 표현한 방법이다. 이를 활용하면 필요에 따라 각 벡터 혹은 벡터가 서로 곱해지는 부분에 가중치를 부여할 수 있다는 장점이 있다. (둘 모두 Luong attention이라고도 불림)
concat attention(Bahdanau attention)의 경우 $h_t$와 $\bar{h}_s$를 concat하여 일반적인 MLP 구조를 통과시킨다고 보면 된다. 2 layer짜리 MLP($W_1$, $W_2$)에서 input으로 concat된 벡터 $\left[ h_t ; \bar{h}_s \right]$가 들어가 linear layer 하나를 통과하게 된다. 여기서 그 linear layer의 가중치 $W_1$의 역할을 $W_a$이 하게 된다. linear layer를 통과하고 나온 출력은 다시 $\tanh$ 활성화 함수를 통과하여 $n$차원의 벡터가 출력으로 나오게 된다. 이 $n$차원 벡터가 $W_2$를 통과하여 최종적으로 1x1 (즉, scalar 값) 크기의 값을 도출하게 된다. 이 식에서 $v_a ^{\intercal}$는 $W_2$를 의미한다. 행렬이 아니라 $v$라는 벡터 형태의 표기를 한 이유는, 어차피 최종적으로 크기 1짜리가 나와야하므로 $W_2$의 shape이 $n \times 1$이기 때문이다.
실제 구현시 한가지 주의할 점은, Luong attention의 경우 먼저 input이 RNN(LSTM 등)을 통과한 후 나온 벡터(hidden state vector)가 context vector와 concat되어 output layer를 통과하는데, Bahdanau attention에서는 이전 hidden state vector가 attention에 먼저 통과되고 이에 대한 output으로 나온 context vector를 input vector와 concat시켜 이를 RNN에 통과시킨다. 순서의 차이가 있으므로 이에 주의하도록 하자.
가장 단순한 모델인 dot attention이 아닌 general attention이나 concat attention의 방법을 활용하게 되면 각 방법에서 사용되는 가중치도 모델 학습시 같이 학습되므로, 보다 의미있는 score 수치를 얻어낼 수 있다는 장점이 있다.
Attention 구조의 특징
- 번역 성능의 향상
- Attention 구조에서는 Encoder의 hidden state vector에 가중 평균을 가하여 구한 벡터를 output을 출력하는 데에 활용한다. 이에 따라 우리는 우리가 원하는 특정 단어에 포커스를 맞추어 보다 중요한 단어를 확실히 번역할 수 있다는 이점을 가져올 수 있다.
- Bottleneck problem 해결
- 앞서 앞 부분 단어에 대한 정보가 뒷부분까지 잘 전달되지 않을 수 있는 문제를 해결하였다.
- 따라서 긴 문장 번역이 보다 수월해진다.
- Backpropagation에서의 이점
- 기존 Encoder-Decoder만 사용하던 구조에서는 Decoder에서 도출되는 loss를 역전파시키기 위해 Decoder sequence에 Encoder sequence를 더한 길이만큼의 역전파를 전달해야만 했다. 이렇게 되면 문장이 조금만 길어져도 긴 timestep을 다 거쳐야해서 아무리 LSTM/GRU를 도입했어도 맨 앞단에서는 역전파의 vanishing 현상이 일어날 수 있다.
- 하지만 attention 구조에서는 역전파 시 긴 sequence를 거칠 필요 없이 attention output을 통해 들어가 맨 앞단에서도 direct하게 역전파를 전달받을 수 있다는 장점이 있다.
- 모델의 해석 가능성(interpretability)을 제시
- AI system에서는 해석 가능성이 존재한다는 점이 매우 큰 강점이 될 수 있는데, 모델의 개선 가능성 및 디버깅이 훨씬 수월해지기 때문이다. (그 외에도 여러 이유가 있을 수 있다)
- 해석 가능성이란 모델이 내놓는 output이나 학습 과정에서 사용되는 파라미터 등이 어떤 식으로 변화하는지, 그래서 최종적으로 왜 모델이 이러한 output을 내놓았는지를 사람이 이해할 수 있는 가능성을 말한다.
- 우리는 attention 단에서 가중 평균이 어떤 식으로 계산되었는지(어느 벡터에 더 가중치가 부여되었는지)를 관찰함으로써 Decoder가 각 timestep에서 어디에 포커싱하였는지를 쉽게 알 수 있다.
- 또한 softmax loss 만으로 내부 모든 모듈이 학습되기 신경망이 언제 어떤 단어를 더 잘 보아야하는지 스스로 학습할 수 있게 된다. (alignment, 즉 단어의 순서를 스스로 학습)
Beam search
Greedy decoding / Exhaustive search
이전에 한번 지적했지만, 지금까지 배운 모델의 형태는 output을 근시안적으로(greedy decoding) 내놓기 때문에, output을 하나만 잘못 내놓아도 그 뒤의 output까지 모두 꼬여버리는 현상이 발생한다. 하지만 뭔가 잘못되었다는 것을 중간에 깨달아도 다시 되돌아갈수는 없다. (추론 과정 중간에 잘못되었다는걸 깨달을 수 있는지도 사실은 잘 모르겠다)
$y$가 출력, $x$가 입력일 때 우리가 본래 원하는 값은 아래 값을 최대화하는 것이다.
다만 이렇게 하려면 모든 가능한 경우의 수를 모두 따져야하는데 시간 복잡도 $O(V ^t)$($V$는 vocabulary의 size)의 연산은 현실적으로 말이 안된다. 따라서 이전에 greedy decoding(최선만을 따지는 방법)과 위와 같은 bruth-force 느낌의 알고리즘(exhaustive search)의 절충안으로 Beam search 알고리즘을 사용하게 된다.
Beam search
Beam search에서는 매 timestep마다 가능한 모든 경우의 수를 따지되, 다음 input으로는 확률값이 높은 상위 $k$개의 갈래(hypothesis)만 넣어주는 방법이다. $k$는 보통 5~10 정도의 값으로 설정한다.
이전과 달리 현재 갈래에서의 확률값을 지속적으로 추적하기 위해 확률값 계산이 동반되어야 하는데, 확률값을 곱하는 연산 대신 역시 이전처럼 아래와 같이 $\log$를 사용하게 된다.
식은 좀 복잡할 수 있는데, 애초에 우리가 사용하는 RNN 모델 자체가 이전 정보를 담고 있는 hidden state vector를 활용하기 때문에 모든 timestep의 output으로부터 조건부 확률을 충족하는 확률 값을 얻을 수 있다.
한편, 확률은 0과 1사이의 값이므로 로그 함수를 취하면 음수가 된다. 다만 로그 함수는 단조증가 함수이기 때문에 음수가 되어도 여전히 가장 큰 값이 searching의 1순위가 된다. (즉, 절댓값이 가장 작은 값, 0에 가까운 값)
Beam search는 무조건 최선의 값을 찾아내지는 못한다. 다만 계산의 효율을 늘리고 기존 greedy한 방법보다는 최선의 결과를 얻을 수 있다.
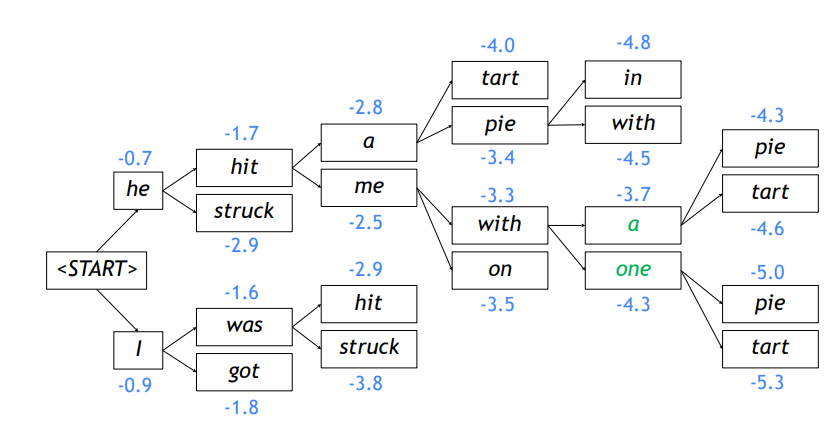 위 그림은 $k=2$일 때의 Beam search를 수행한 예시이다.
첫 단계를 제외한 매 timestep에서 $k$개의 갈래로부터 다시 각각 $k$개의 갈래를 생성해내므로 $k^2$ 만큼의 연산을 수행하게 된다.
다만 이중에서 다시 최선의 $k$개를 선택하게 되므로 그 크기가 축소된다.
매 순간 가장 확률 값이 높은 갈래만을 선택하여 알고리즘이 수행되는 것을 확인할 수 있다.
위 그림은 $k=2$일 때의 Beam search를 수행한 예시이다.
첫 단계를 제외한 매 timestep에서 $k$개의 갈래로부터 다시 각각 $k$개의 갈래를 생성해내므로 $k^2$ 만큼의 연산을 수행하게 된다.
다만 이중에서 다시 최선의 $k$개를 선택하게 되므로 그 크기가 축소된다.
매 순간 가장 확률 값이 높은 갈래만을 선택하여 알고리즘이 수행되는 것을 확인할 수 있다.
다만 Beam search에서는 ’<EoS>’ 토큰의 위치가 불분명하므로 갈래마다 EOS 토큰이 생성되는 시점이 다를 수 있다. EOS 토큰이 생성되면 해당 hyphothesis는 종료되어 따로 저장공간에 저장해놓고 남은 다른 task를 수행한다.
Beam search는 미리 정해둔 timestep $T$에 도달하거나 미리 정해둔 $n$개의 완료된 문장이 생성되면 알고리즘이 종료된다. (종료되는 시점은 $k$ 자체와는 큰 관련이 없다는 점에 주의하자.)
알고리즘이 종료되면 저장된 completed hyphothesis에서 다시 가장 높은 확률 값을 가진 hyphothesis를 선택하여 최종적으로 출력으로 내보낸다. 그런데 확률의 로그 값은 항상 음수이므로 sequence의 길이가 길어질수록 반드시 확률 값이 낮아진다는 문제가 존재한다. 따라서 아래와 같이 sequence의 길이로 score 값을 나누어 normalize된 값이 최종 candidate score가 된다.
BLEU
자연어 생성 모델(i.e. 번역 모델)의 평가는 어떤 방식으로 이루어질까? 단순히 ‘해당 위치에 해당 단어가 있어야 한다’라는 기준으로 평가를 하면, output이 하나라도 더 생성되거나 덜 생성되는 순간 이후 sequence는 모두 틀린 것으로 처리된다. 그렇다면 reference(target)의 단어와 몇 개나 일치하는지에 초점을 두고 평가해볼 수 있다.
Precision/Recall, F-measure
아래와 같이 정밀도와 재현율을 생각해볼 수 있다.

precision(정밀도)은 보이는 것으로 판단할 수 있는 수치이다. 검색을 예로 들면, 어떤 키워드로 검색을 했을 때 우리는 그 중 원하는 정보가 몇 개인지 전체 검색 결과에 대하여 percentage를 측정할 수 있다. 즉, 예측된 결과의 크기와 우리가 원하는 정보량의 비를 측정할 수 있으며, 이것이 정밀도이다.
recall(재현율)은 실제로 잘 된건지 전지적 시점에서 판단할 수 있는 수치이다. 어떤 키워드로 검색했을 때 원래 나와야 할 정보가 100개인데 그 중 5개만 나왔다고 해도 우리는 그 수치를 직접 판단할 수 없다. 이렇게 판단할 수 없는 수치를 재현율로 나타내며, 이는 실제 나와야할 결과의 크기와 맞게 나온 정보량의 비로 나타낸다.
정밀도와 재현율은 둘다 중요한 수치로, 둘 모두 높은 결과를 낼 수 있는 모델이 좋은 모델일 것이다. 이러한 배경에서 둘 모두를 고려할 수 있도록 계산된 값이 바로 F-measure으로, 이는 정밀도와 재현율의 조화평균이다.
참고로, 산술-기하-조화 평균의 관계는 아래와 같다. (2변수 기준)
기하학적으로 산술평균은 두 점 사이의 중점을 의미하며, 기하평균은 그보다 작은 값 쪽으로 더 치우친 점, 조화평균은 기하평균보다도 더 작은 쪽으로 치우친 점을 의미한다. 즉, 산술-기하-조화로 흐를 수록 그 평균값은 작은 값에 큰 가중치를 준 내분점이 된다.
F-measure(이하 F1 score)는 정밀도와 재현율 중 더 작은 값에 가중치를 준 평균값이 된다.
하지만 위와 같이 F-measure만을 평가하게 되면 또 다른 문제점이 발생하는데, 순서(order)가 맞지 않는 문장에 패널티를 주는 것이 불가능하다. 단어는 모두 일치하는데 순서가 완전히 뒤바뀐 문장이 생성될 경우 F-measure가 100%로 계산되겠지만, 이는 우리가 원하는 형태가 아니다.
BLEU score
BLEU(BiLingual Evaluation Understudy)는 N-gram overlap을 활용한 수치를 추가적으로 사용하여 순서 및 F-measure에 준하는 수치를 동시에 평가할 수 있다. n-gram은 연속된 $n$개의 단어가 reference(target) 문장에 존재하는지를 평가하는 수치로, $n$은 보통 1부터 4까지의 수를 모두 활용한다.
우리가 구하고자 하는 값은, $1 \leq n \leq 4$인 $n$에 대한 n-gram의 precision 수치를 모두 곱하는 것이다. 한편, 동시에 생성된 단어의 수가 reference(target) 문장만큼은 되는지를 평가하기 위해 brevity penalty 수치를 함께 활용한다.
recall 수치는 여기서 직접적으로 사용되지 않는다는 점을 확인할 수 있는데, 다음과 같은 이유를 들 수 있다.
- 원래 문장에서 단어가 몇 개 빠지더라도 의미가 일맥상통할 수 있다.
- i.e. ‘나는 너무 너무 기쁘다’와 ‘나는 너무 기쁘다’는 비슷한 의미이다.
- BLEU에서는 이미 recall에 준하는 수치를 활용하고 있다.
- brevity penalty에서는 reference 문장의 길이 정보를 활용하는데, 이는 recall의 특성을 반영하는 한편 recall을 보다 단순화한 형태라고 이해할 수 있다.
BLEU score는 보통 한 개의 single sentence가 아닌 전체 말뭉치(corpus)에 대해 계산되며, 여기서는 precision중 작은 값에 지나친 가중치를 주지 않기 위해 기존 조화평균 대신 기하평균을 사용한다.
적용 예시
- Reference(ground truth): Half of my heart is in Havana ooh nana
- Predicted(from model 1): Half as my heart is in Obama ooh na
- Predicted(from model 2): Havana na in heart my is Half ooh of na
model 2는 F-measure 기준 100%의 정확도를 가짐에도 불구하고, 아래와 같이 BLEU에서는 0%의 정확도를 가진다.
| Metric | Model 1 | Model 2 |
|---|---|---|
| Precision(1-gram) | $\frac{7}{9}$ | $\frac{10}{10}$ |
| Precision(2-gram) | $\frac{4}{8}$ | $\frac{0}{9}$ |
| Precision(3-gram) | $\frac{2}{7}$ | $\frac{0}{8}$ |
| Precision(4-gram) | $\frac{1}{6}$ | $\frac{0}{7}$ |
| Brevity penalty | $\frac{9}{10}$ | $\frac{10}{10}$ |
| BLEU | $0.9 \times \sqrt{3} / 3 =52\%$ | $0$ |
Reference
Natural Language Processing with Deep Learning CS224N/Ling284
OpenNMT Beam search