Day11. 베이즈 정리, PyTorch, 머신러닝의 역사

베이즈 통계학과 딥러닝의 역사적 흐름, PyTorch, MLP

Posted by MoonJaeHoon on February 01, 2021 · 13 mins read

개요

오늘 다룬 내용은 상당히 광범위했다. 그래서 양 자체는 많은데, 다행히 어려운 부분은 적었기 때문에 오늘도 기억할 부분 위주로 정리하려고 한다.

오늘 배운 내용은 아래와 같다.


베이즈 통계학

베이즈 통계학에서는 사전 확률에 대하여 새로 발생한 사건을 근거로 사후 확률을 갱신한다.
최근 많은 머신러닝이 베이즈 통계학을 기반으로 돌아간다. 이전에 계산된 사후 확률이 이후의 사전 확률으로 쓰일 수 있기 때문이다.
따라서 잘 이해하고 넘어가도록 하자.

베이즈 정리

베이즈 통계학에서 사후확률과 사전확률 사이의 관계식은 아래와 같다.

$$ P(\theta \vert \mathcal{D}) = P(\theta) \frac{P(\mathcal{D} \vert \theta)}{P(\mathcal{D})} $$

여기서 좌변은 사후확률(Posterior), 우측의 $P(\theta)$는 사전확률(Prior)을 의미한다. 또한 $P(\mathcal{D})$는 새로 관측된 증거(Evidence)(=정보)이다. $P(\mathcal{D} \vert \theta)$는 이전에 배웠던 가능도로, 현재 주어진 모수(가정)에서 이 데이터가 관찰될 확률을 의미한다. 알고있는 내용이니 자세한 설명은 생략한다.

아래 문제를 보면 이 식이 어떤 프로세스로 동작하는지 파악할 수 있다.

어떤 병의 발병률이 10%로 알려져있다. 이 병에 실제로 걸렸을 때 걸렸다고 검진될 확률은 99%이고, 실제로 걸리지 않았을 때 오검진될 확률이 1%라고 할 때, 어떤 사람이 이 병에 걸렸다고 검진결과가 나왔을 때 정말로 병에 걸렸을 확률은?

중요한 것은 아래 관계를 파악해서 이용하는 것이고, 다른 내용은 알기 쉬우니 생략한다.

$$ P(\mathcal{D}) = \sum\limits _{\theta} P(\mathcal{D} \vert \theta)P(\mathcal{\theta}) = P(\mathcal{D} \vert \theta)P(\mathcal{\theta}) + P(\mathcal{D} \vert \theta ^\text{C})P(\mathcal{\theta ^\text{C}}) $$

계산해보면 약 0.916의 확률이 나온다. 여기까지는 그냥 하면 되고 이제 문제를 좀 변형해서 값이 얼마나 바뀌는지 파악해보자.

만약 이 병에 걸리지 않았는데 오검진될 확률이 1%가 아닌 10%라고 해보자. 이렇게 하면 확률이 0.524로 급격하게 떨어진다.
이와 같이 오탐율(False alarm)이 올라가면 테스트의 정밀도가 급격하게 떨어진다는 점을 기억하자.

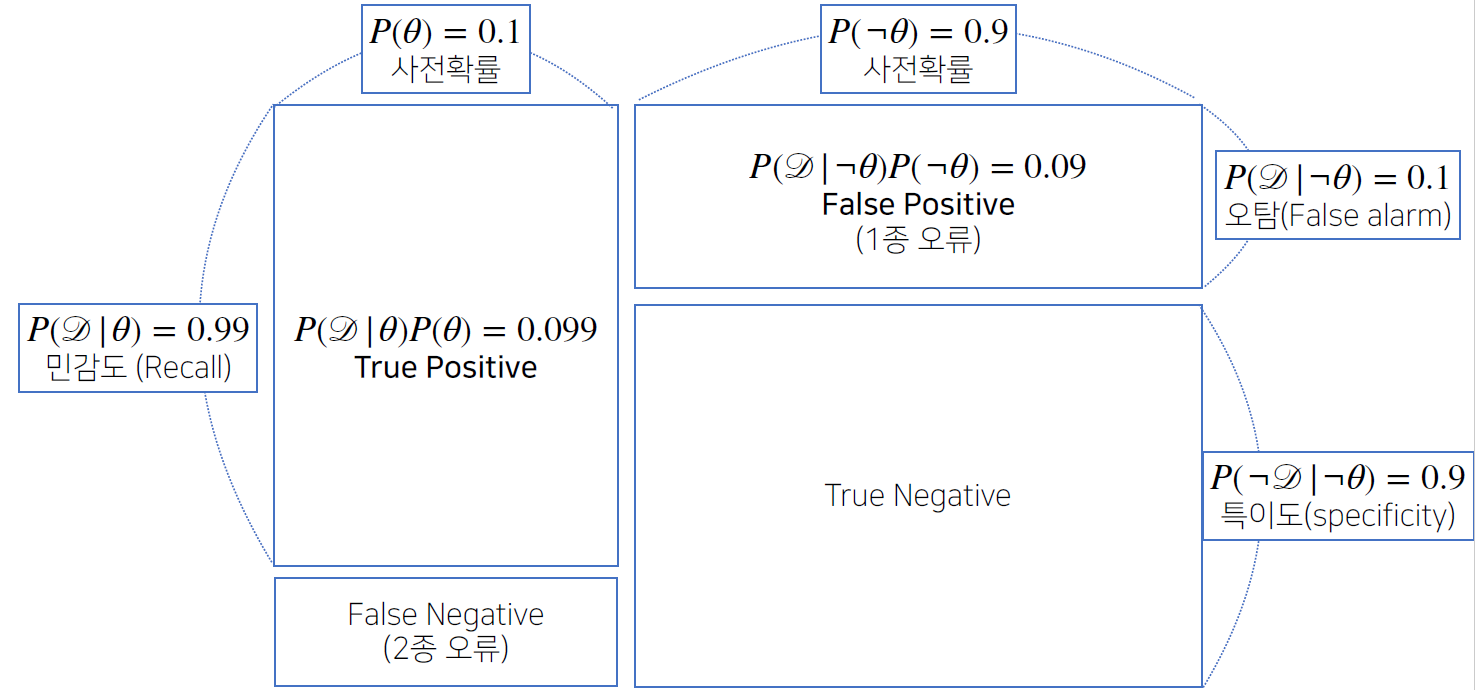
conditional
위 그림은 오탐율 1%일 때의 조건부확률들을 시각화 한것으로, True Positive는 병이 있고 양성일 확률, True Negative는 병이 없고 음성일 확률이다.
False Negative는 병이 있고 음성일 확률, False Positive는 병이 없고 양성일 확률이다. 그림에서 각각이 2종 오류, 1종 오류라고 써져있는데 이들 용어를 잘 정리해두자.

머신러닝에서 베이즈 정리가 많이 쓰이는 이유는 이전에 구한 사후 확률을 다음의 사전 확률로 사용할 수 있기 때문이다.

만약 오탐율을 10%라고 하고 딸림문제를 아래와 같이 설정하면,

앞서 양성 판정을 받은 사람이 두 번째 검진을 받았을 때도 양성 판정을 받았을 때 이 사람이 진짜 이 병에 걸렸을 확률은?

0.524였던 확률이 약 0.917으로 다시 급격히 올라가게 되는 것을 확인할 수 있다. (자세한 계산은 생략)

인과 관계

조건부 확률은 유용한 통계적 해석을 제공하지만 인과관계(causality)를 추론할 때 이를 함부로 사용해서는 안된다.
인과관계는 데이터 분포의 변화에 강건한(즉, 시나리오에 따른 확률 변화가 적은) 예측모형을 만들 때 필요하다.
조건부 확률 기반 예측 모형은 아래와 같이 시나리오에 따라 확률변화가 매우 크지만 인과 관계 기반 예측 모형은 여러 시나리오에 대해 예측 정확도가 안정적이다.

causality

다만 보다시피 인과 관계만으로는 높은 정확도가 보장되지 않는다.
또한 인과관계를 알아내기 위해서는 중첩요인(confounding factor)의 효과를 제거하고 원인에 해당하는 변수만의 인과관계를 계산해야 한다.

예를 들어, ‘키가 크다’->’지능이 높다’는 별 관계가 없어보이지만 실제로 분석을 해보면 데이터상으로 이 관계는 성립한다.
하지만 우리는 이 둘의 인과관계를 파악할 때 중첩요인인 ‘나이’를 제거하지 않았다. 이렇게 중첩요인을 제거하지않으면 가짜 연관성(spurious correlation)이 나오게 된다.
참고로, 여기서 키와 지능은 상관관계가 있으나, 인과관계는 없는 것이다. 둘의 차이점을 명확히 이해하고 넘어가자.

아래는 비슷한 일례로 심슨의 역설을 보여주는 문제이다.
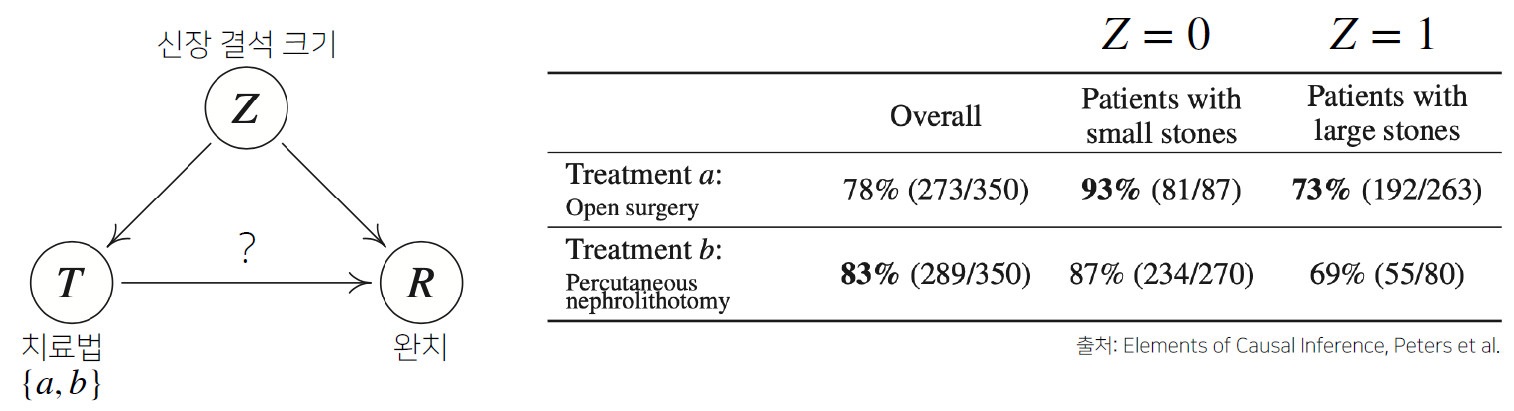
simpsons_paradox
분명 Z=0, Z=1 모두에서 치료법 a가 더 높은 치료율을 보여주지만 합산치로 보면 b가 더 높은 치료율을 보인다.

이러한 문제는 $\text{do}(T=a)$라는 조정(intervention) 효과를 통해 혼재변수 $Z$의 개입을 제거함으로써 해결할 수 있다. 실제로 개입을 제거하고 계산한 결과는 a가 약 0.8325, b가 약 0.7789의 치료율로 a의 치료율이 더 높은 것으로 판단할 수 있다.


PyTorch

현재를 기준으로 가장 많이 쓰이는 딥러닝 프레임워크는 Tensorflow와 PyTorch이다.

둘 모두 장단점이 있다고 하는데, 강의해주시는 교수님께서는 논문 쓸 때는 PyTorch, 서비스 런칭시에는 Tensorflow를 많이 사용하신다고 한다.
아직 제대로 배우지는 않아서 정확한 장단점이나 위와 같이 프레임워크를 복합적으로 사용하시는 이유는 잘 모르겠다. :no_mouth:

아무튼 우리가 앞으로 배울 것은 PyTorch이다.
PyTorch는 크게보면 Numpy + AutoGrad(자동 미분) + Function으로 이루어진다.
PyTorch 역시 Numpy 구조를 가지는 Tensor 객체로 array를 표현한다. 다만 완전히 ndarray 구조는 아니기 때문에 실사용시 상호변환이 필요하기는 하다.
무료로 제공되는 전자책으로 PyTorch로 시작하는 딥러닝 입문이 좋은 듯하니 시간 날 때마다 읽어봐야겠다.

PyTorch에서의 문법을 아~주 간단하게 보면 numpy와 대부분이 비슷한데, 일단은 아래 3가지만 숙지하고 가자.

  • numpy에서의 dot()이 PyTorch에서는 matmul()이다. 표현이 더 직관적인 것 같다.
  • numpy에서의 reshape()이 PyTorch에서는 view()이다. 이건 오히려 직관성면에서는 퇴보했다. :sweat:
  • 그 외 squeeze()로 랭크 축소, unsqueeze()로 랭크 확장을 할 수 있다.

가장 중요한 것은 처음보는 클래스/함수들은 직접 깃허브에서 코드를 따고 들어가 살펴보는 것이다.
오늘 실습할 때도 실제로 그렇게 몇 번 해봤는데 정말 도움되고 이해도 더 잘되는 것 같다.
시간이 없다면 적어도 각 class의 attribute가 무엇을 의미하는지, 각 메소드의 parameter로 들어가는게 무엇을 의미하는지정도는 분명히 확인해볼 가치가 있다.


딥러닝의 역사

솔직히 이 부분은 들어도 아직 모르는게 당연하긴한데, 적어도 역사적 흐름 정도와 나중에 읽어볼 논문들을 살펴보는 정도에 의의를 두고 넘어가려고 한다.
머신러닝 역사가 제대로 시작된지는 얼마 안되었기 때문에 역사가 짧다는 것이 장점 :sunglasses: 이라면 장점이다.

기본 프로세스

  • 기본적인 연구/논문의 process는 데이터수집 -> 모델 설계 -> 손실 함수 설계 -> 알고리즘 설계로 이루어진다.
    실제 논문을 읽을 때도 이를 염두해두고 읽으면 좋을듯하다.
    1. 데이터
      • 데이터는 우리가 풀고자하는 문제에 맞는 데이터로 준비한다.
      • 예를 들어 비전이라는 같은 대주제에 대해 연구하더라도 소주제가 당연히 모두 다르니(classification, semantic segmentation, detection, pose estimation, visual QnA, …) 이에 맞게 전처리 혹은 라벨링이 필요하다.
    2. 모델
      • 문제를 풀기 위한 모델을 설계한다. 흔히 아는 AlexNet, ResNet, GAN 등이 모델에 해당한다.
    3. 손실함수
      • 우리가 풀고자하는 문제가 곧 손실함수이다.
      • 손실함수를 쓸 때마다 왜 이 손실함수를 이 문제를 풀기 위해 사용하는지를 늘 고민해보아야 한다.
      • 그리고 당연히, loss function을 최소화한다고 꼭 우리가 원하는걸 이루는 것은 아니다. 과적합 등의 문제가 발생할 수 있다.
      • 대표적인 3문제를 예로 들자면, Regression에서는 mean squared error(MSE), Classification에서는 cross entropy(CE), Probabilistic에서는 maximum likelihood estimation(MLE)를 손실함수로써 사용한다.
    4. 알고리즘
      • 즉, 손실함수를 빠르게(혹은 자원을 덜 쓰고) 최적화하는 알고리즘을 설계해야한다.
      • Gradient descent도 이의 일종이고, SGD, Adam 등도 있으며 이런거 말고도 데이터 설계 측면에서의 최적화도 있는 것 같은데 그건 아직 잘 모르겠다 :confused:

역사

  1. 2012년 ImageNet 콘테스트에서 처음으로 AI를 활용한 모델이 우승하였으며 이것이 흔히 알려진 AlexNet이다. 딥러닝의 역사는 사실상 여기서부터 시작된다.
  2. 2013년 알파고로 잘 알려진 Deepmind에서 DQN이라는 개념을 발표한다. DQN은 CNN을 응용한 네트워크이다.
  3. 2014년 Encoder/Decoder 구조가 쓰이면서 NLP 분야가 발달하기 시작했다.
  4. 2014년 Adam Optimizer가 발표되었고, 이것을 아직도 많이들 사용한다. 일단 성능이 제일 좋고,
    • 여담으로, 실제로 많은 논문에서는 여러 알고리즘의 hyper parameter를 조정해서 높은 정확도를 보이는 경우가 잦은데, 중요한건 이에 대한 이유를 거의 설명하지 않고 있으며 다수의 실험을 통해 얻은 결과로 추측된다.
    • 그런데 hyper parameter를 매번 조정해가면서 여러번 모델을 돌리는 것은 장비가 수없이 많지 않은 이상 쉽지 않은 일이다.
    • 그래서 대부분의 일반인들은 보통 가장 성능이 좋다고 알려진 Adam Optimizer를 사용한다.
  5. 2015년 Generative Adversarial Network(GAN)은 데이터 생성기와 식별기가 서로 제로섬게임하며 학습을 하는 모델이다.
    이게 여기에 쓰기엔 내 이해도가 부족한 것 같은데, 찾아보니까 되게 재밌는 모델인 것 같다. 아래 레퍼런스에 관련 글을 달아두었다.
    아무튼 현재까지도 이에 대한 논문이 쏟아지고 있다고 하니, 실제로 파급력이 큰 모델이었던 것 같다.
  6. 2015년 Residual Networks은 NN에 층이 너무 깊게 쌓이면 과적합 등의 오류가 발생할 수 있다는 편견(?)을 깨고 깊게 층을 쌓은 첫 모델이라고 한다.
  7. 2017년 Transformer 아직 뭔지는 모르겠으나 현재 이 구조가 웬만한 Neural 구조를 다 잡아먹고 있다고 한다. Attention 구조라고도 불린다.
  8. 2018년 BERT NLP 분야에서 온갖 말뭉치를 다 끌어모아 fine-tuning을 하게 하는 모델이다.
  9. 2019년 BIG Language Models는 BERT(fined-tuning NLP)의 발전된 모델로, parameter 개수가 무려 천 억이 넘는다.
  10. 2020년 Self Supervised Learning은 학습 데이터 외에 라벨 모르는 비지도 학습 데이터를 지도 학습에도 이용하는 모델이라고 한다. 맞게 이해한건진 모르겠지만..
    그 외에도 최근에는 새로운 dataset을 인공적으로 만드는 연구도 활발하게 이루어지고 있다.

딥러닝이 출범한지 얼마 되지 않아 2021년에는 또 어떤 패러다임이 제시될지 모두의 기대가 클 것이라 생각한다.
보면 알겠지만 거의 1년 간격으로 새로운 성과들이 속속들이 발표되는데, 그만큼 이 분야에 종사하려면 계속해서 공부하는 것이 더욱 중요한 것 같다.


MLP

뉴럴 네트워크(Neural Network)는 인간의 신경망 구조를 표방해서 말한 것이라고 하지만, 사실 더 정확히 말하면 이건 현실 세계와 근사하도록 만든 일종의 함수이기도 하다.

Neural networks are function approximations that stack affine transformations followed by nonlinear transformations.

여기서 말하는 affine transformation은 차원 변환을 말하는데, 한 마디로 비선형변환이 있는 다층의 차원변환 함수가 바로 NN이라는 것이다.

뉴럴 네트워크에서는 가중치 행렬을 곱해주고 비선형 변환(activation function) 후 다시 다음 층을 통과한다. 이 일련의 과정이 위 한 문장에 축약되어 담겨있다. 같은 맥락에서, 뉴럴 네트워크에서의 행렬은 서로 다른 두 벡터 공간 사이의 매핑이라고 간주할 수 있다.

참고로, Multilayer feedforward networks are universal approximators 논문에 따르면 모든 measurable function은 한 개의 은닉층으로 반드시 표현될 수 있다.
다만 이는 어디까지나 존재성이 밝혀진 것이지, 어떻게 찾는지도 중요한 요소이기 때문에 실제로는 싱글 레이어만으로 뉴럴 네트워크를 구성하지는 않는다.

MLP에 대한 실습도 MNIST 데이터로 간단하게 진행해보았다.
여기에 코드를 담지는 않지만 간단한 프로세스정도만 남겨두려고 한다.

  1. device로 GPU 혹은 CPU를 지정한다.
  2. 데이터 셋을 불러와서 배치 사이즈를 지정하고 이를 기반으로 데이터를 나눈다.
    • 만약 이 과정을 하지 않으면, 데이터가 매우 많을 때 메모리에 데이터를 모두 올릴 수 없기 때문에 학습을 할 수 없다.
    • 또한, 이 과정에서 data shuffle도 반드시 해주어야한다.
  3. MLP 클래스를 정의하여 layer 층을 구성하고 loss function을 설계하고 optimizer를 고른다.
    • 이 때, 입력층과 출력층의 행/열 개수를 반드시 의도와 맞게 설정해야한다.
    • MLP클래스에 torch.nn.Linear객체를 원하는 층 개수만큼 레이어 역할로 넣어주는데 이 때 파라미터로 위에서 말한 행/열 개수를 설정한다. 가중치는 nn.Module(이걸 MLP 클래스가 상속받았다)에서 미리 구현된 init_param()으로 초기화해준다.
    • 최종 out은 0~9이니까 10개가 확정이고, 여기서는 입력층을 28*28(픽셀수인것 같다)로 설정하였다. (중간 레이어는 알아서 설정..?)
    • MNIST는 전형적인 classification 문제로, cross entropy를 loss function으로 설계한다.
    • 앞서 말했듯이 optimizer는 무난한 Adam을 사용하였다.
  4. 벌써 앞서 말한 데이터 정리, 모델 설계, 손실 함수 설정, 옵티마이저 설정까지 다 끝났다.
    이제 파라미터를 초기화해주고(init_param()) 학습을 돌리면 된다.
    • 학습 전에 EPOCH 수치를 설정하고 그 수치만큼 같은 데이터로 여러 번 학습을 돌려주는데, 1 EPOCH는 모든 train data를 한 번 다 돈다는 것을 의미한다.

전체 코드도 길이는 긴데 간단한 편이라 이해가 다 돼서 따로 적진 않으려고 한다.
하지만 이해만 될 뿐이지 이 프로세스에 익숙해지는 데에는 오래 걸릴 듯하니 기억할 것은 잘 기억해두자.


데이터 가공

학습을 하기 위해서는 데이터 셋을 세팅하는 것이 가장 중요하며, 이를 위한 클래스가 PyTorch에서도 정의되어있다. (torch.utils.data.Dataset)
이 데이터셋을 이용하여 데이터를 벡터화해서 불러오고, 데이터 이터레이터를 반환받을 수 있다. 그리고 이러한 클래스를 상속받아서 커스텀 데이터셋을 만들 줄 알아야한다.

일단 이를 위해 Dataset 클래스의 구조를 파악해야하는데, 요약하면 프로세스는 다음과 같다.

  1. Dataset 클래스를 상속받는 새로운 커스텀 클래스를 정의
  2. train boolean 설정, download 등을 담당하는 __init__, 전처리를 해주는(이미지를 벡터화 등 => PIL lib 이용) __getitem__ 메소드를 구성한다.
  3. Dataset 클래스를 이용하여 데이터 iterator (DataLoader) 불러오기
  4. iterator를 이용하여 학습 진행

사실 그냥 보면 굉장히 간단할 것 같은데, Dataset 클래스의 구조를 잘 파악하고 있어야만 커스텀 데이터셋도 만들 수 있다.
그리고 그 Dataset 클래스 구조가 좀 복잡한 편이다 (…)

일단 내용은 이게 다이다. 이 부분은 추후 연습을 하면서 메꿔나가야 할 것 같다.
오늘은 시간이 부족하여 :cry: 당장 연습은 어렵고, 주말즈음에 커스텀 Dataset을 구성하는 연습을 해보아야겠다.

(예정)
이 링크에서 PyTorch의 Dataset 클래스에 대해 좀 더 세부적으로 익히고, 여기서 특히 이미지 데이터셋을 어떻게 만드는지 배운 후 notMNIST 데이터를 이용하여 커스텀 데이터셋을 만들어 기존에 MNIST 학습에 이용했었던 코드에 한번 적용해보고자 한다.


Reference

고전 통계학과 베이지안 통계학
심슨의 역설
Generative Adversarial Network(GAN)
Epoch, Batch size, iteraion

← Previous Post Next Post →